B1nсоставляющейи вектором B1 индукции магнитного поля в среде магнетикаμ1 магнитной проницаемостью, а также α2 угол между нормальной B2nсоставляющейи вектором 1 страница

Лекция 8. Магнитное поле в веществе

Намагниченность вещества. Связь молекулярных токов в магнетике с намагниченностью в интегральном виде. Связь молекулярных токов в магнетике с намагниченностью в дифференциальном виде. Вектор напряженности магнитного поля и его связь с векторами индукции и намагниченности. Теорема о циркуляции вектора напряжённости магнитного поля в дифференциальном и интегральном видах. Магнитная восприимчивость и магнитная проницаемость. Диамагнетики, парамагнетики и ферромагнетики. Нормальные составляющие вектора напряжённости и индукции магнитного поля на границе раздела магнетиков. Тангенциальные составляющие вектора напряжённости и индукции магнитного поля на границе раздела магнетиков. Магнитное поле проводника с током в вакууме и при заполнении пространства, окружающего его, однородным непроводящим магнетиком.

Физическая природа диамагнетизма. Физическая природа парамагнетизма. Ферромагнетики: зависимость индукции, намагниченности и магнитной проницаемости ферромагнетика от напряжённости внешнего магнитного поля; петля гистерезиса. Магнитострикция.

Намагниченность вещества, находящегося во внешнем магнитном поле

Если несущие ток проводники находятся в какой-либо среде, магнитное поле изменяется. Это объясняется тем, что всякое вещество является магнетиком, т. е. способно под действием магнитного поля приобретать магнитный момент или намагничиваться. Намагниченное вещество создаёт магнитное поле с вектором B' индукции, которое накладывается на обусловленное токами в проводниках магнитное поле с вектором B₀ индукции. Оба магнитных поля дают в сумме следующий результирующий вектор B индукции магнитного поля: B = B₀ + B'. (7. 103) Под действием вектора B₀ индукции внешнего магнитного поля векторы p _m магнитных моментов молекул приобретают преимущественную ориентацию в одном направлении, вследствие чего магнетик намагничивается, т. е. его собственный суммарный вектор B' индукции магнитного поля становится отличным от нуля. Вектор J намагниченности в Δ V малом объёме, взятый в окрестности рассматриваемой точки, равен сумме векторов p _m магнитных моментов отдельных молекул, поделённых на этот Δ V малый объём, вследствие чего для вектора J намагниченности имеет место следующее выражение: J = ∑ p _m / Δ V, (7. 104) Δ V

т. е. вектор J намагниченности магнетика равен сумме векторов p _m магнитных моментов отдельных молекул, находящихся в единице объёма этого магнетика.

Связь молекулярных токов в магнетике с намагниченностью в интегральном виде

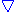
Ротор (7. 30) из раздела 7. 1 " Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях " результирующего вектора B индукции магнитного поля в произвольной точке пространства с учётом (7. 103) имеет следующий вид: [ B ] = [ B ₀ ] + [ B']. (7. 105) Согласно(7. 30) из раздела 7. 1 " Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях " [ B ₀ ] = μ ₀ jротор вектора B₀ индукции внешнего магнитного поля в произвольной точке пространства, занятого магнетиком, пропорционален вектору j плотности макроскопического или тока проводимости в этой точке пространства. Аналогично (7. 30) из раздела 7. 1 " Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях " [ B ' ] ротор собственного суммарного вектора B' индукции магнитного поля в произвольной точке пространства, занятого магнетиком, пропорционален вектору j_мол плотности молекулярных токов в этой точке пространства, вследствие чего [ B ' ] ротор собственного суммарного вектораB' магнитной индукции поля имеет следующий вид: [ B'] = μ ₀ j _мол.(7. 106) Подставляем (7. 30) из раздела 7. 1 " Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях " (7. 106) в (7. 105) и получаем, что [ B] ротор

результирующего вектора B индукции магнитного поля в произвольной точке пространства, занятого магнетиком, пропорционален сумме векторов плотностей j макроскопического и

j_мол молекулярного токов, вследствие чего [ B] ротор (7. 105) результирующего вектора B индукции магнитного поля в произвольной точке пространства, занятого магнетиком, имеет следующий вид:

[ B ] = μ ₀( j + j _мол). (7. 107) На рис. 7. 25 изображена область магнетика, а в материале этого магнетика проведён воображаемый Г контур, ограничивающий поверхность S площадью в магнетике в OXY плоскости.

Молекулярные токи I_i_молсилой каждой молекулы текут по окружностям в OYZ плоскости, изображённым на рис. 7. 18 синими окружностями. Эти молекулярные токи I_i_молсилой создают магнитные p _im молекулярные моменты, которые в отсутствие вектора B ₀индукции внешнего магнитного поля направлены хаотично, а при его наличии либо имеют направление, совпадающее с направлением вектора B ₀ индукции внешнего магнитного поля, - это парамагнетики, либо имеют направление, противоположное с направлением вектора B₀ индукции внешнего магнитного поля, - это диамагнетики. Результирующий молекулярный ток I_молсилой ток через поверхность

S площадью, ограниченной воображаемымГ контуром, создают те молекулярныетоки I_i_молсилой, которые пересекают эту поверхность S площадью. Места пересечений магнетика молекулярнымитоками I_i_молсилой площадью отмечены на рис. 7. 18 красными овалами. Молекулярный результирующийток I_молсилой в магнетикеток через поверхность S площадью, ограниченной воображаемым Г контуром, будут создавать лишь темолекулярные токи I_i_молсилой, траекториидвижения которых по окружности

оказываются " нанизанными" на воображаемый Г контур. На рис. 7. 25 эти молекулярные токи обозначенытоком I_i_мол'силой. Молекулярные токи I_i_мол'' силой, которые пересекают в магнетике поверхность S площадью, ограниченной воображаемым Г контуром, дважды, т. е. один раз снизу и один раз сверху, не будут вносить вклад в результирующий молекулярный ток I_молсилой, т. к. алгебраическая сумма таких токов при пересечении поверхности S площадью, будет равна нулю.

Результирующий молекулярный ток I_молсилой в магнетике через поверхность S площадью, которую ограничивает воображаемый Г контур, имеет следующий вид: I_мол = ∫ j_мол d S , (7. 108) S

где S - площадь (рис. 7. 25) поверхности в магнетике, " натянутая" на воображаемый Г контур.

В выражении (7. 108) из результирующего молекулярного тока I_молсилой исключаются молекулярные токи I_i_мол'' силой, которые пересекают в магнетике поверхность S площадью, " натянутой" на воображаемый Г контур, дважды, вследствие попеременного одинакового и противоположного направления единичного n нормального вектора к элементарным поверхностям

dS площадью, в пределах которой определяется молекулярный ток с вектором j_мол плотности. Поэтому молекулярные токи I_i_мол'' силой, текущие через поверхность S площадью, а не по воображаемому Г контуру, в результирующий молекулярный ток I_молсилой вклада не вносят. Результирующий молекулярный ток I_молсилой через поверхность S площадью образуют молекулярные токи I_i_мол' силой, траектории движения которых по окружности оказываются

(рис. 7. 25) " нанизанными" на воображаемый Г контур.

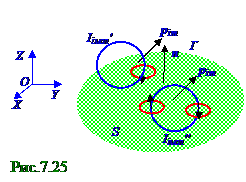
Перед (рис. 7. 26) и за плоскостью чертежа находится магнетик, верхняя и нижняя части которого разделены воображаемым Г контуром, находящимся в OYZ плоскости. Малая dl часть воображаемого Г контура является осью воображаемого косого цилиндра, изображенного на

рис. 7. 26 штрих - пунктирными красными линиями, основания которого п ерпендикулярны (7. 104) вектору J намагниченности в магнетике, коллинеарного магнитным p _im молекулярным моментам каждой молекулы и направленного в парамагнетике по вектору B ₀индукции внешнего магнитного поля, либо в диамагнетике против направления вектора B ₀ индукции внешнего магнитного поля. Площадь основания воображаемого косого цилиндра равна S_молплощади круга, по окружности которого текут молекулярные токи I_i_мол' силой.

Все N молекул, которые обозначены на рис. 7. 26 чёрными точками, попавшие в V объём воображаемого косого цилиндра, пересекают траекториями своих молекулярных токов I_i_мол' силой в местах, отмеченных на рис. 7. 26 красными овалами, поверхность магнетика в плоскости чертежа один раз ниже воображаемого Г контура. Т. е. траектории движения этих токов I_i_мол' силой, изображённые на рис. 7. 26 синими овалами, оказываются " нанизанными" на воображаемый

Г контур. Поэтому результирующий молекулярный ток I_молсилой на рис. 7. 19 в магнетике,

ограниченном воображаемым Г контуром, будут создавать молекулярные токи I_i_мол' силой, траектории движения которых оказываются " нанизанными" на этот воображаемый Г контур. Проекция S_мол┴ площади S_мол основания (рис. 7. 26) воображаемого косого цилиндра на плоскость, перпендикулярную его dl оси имеет следующий вид: S_мол┴= S_молcosα , (7. 109) где α - угол между вектором J намагниченности и dl осью воображаемого, косого цилиндра, который равен, вследствие перпендикулярности вектора J намагниченности плоскостям вращения молекулярных токов I_i_мол' силой, α углу между основанием воображаемого равновеликого прямого цилиндра и основанием воображаемого косого цилиндра.

Объём V (рис. 7. 26) воображаемого косого цилиндра определим с учётом равенства его объёму равновеликого воображаемого прямого цилиндра с S_мол┴площадью основания (7. 109) и

dl длиной, вследствие чего V объём воображаемого косого цилиндра имеет следующий вид: V = S_мол┴dl = S_молdlcosα . (7. 110)

Количество N молекул, попавших в V объём (рис. 7. 26) воображаемого косого цилиндра, с учётом их n концентрации и (7. 78) значения этогоV объёма воображаемого косого цилиндра имеет следующий вид: N = nV = nS_молlcosα . (7. 111)Суммарный I_мол_Vмолекулярныйток всех N молекул, попавших в V объём (рис. 7. 26) воображаемого косого цилиндра, с учётом молекулярноготока I_i_мол'силой каждой из этих молекул, пересекающего V объём

воображаемого косого цилиндра один раз, а также с учётом (7. 110) имеет следующий вид: I_мол_V = I_i_мол'N = I_i_мол'nS_молdlcosα . (7. 112) В (7. 112) произведение I_i_мол'S_мол представляет собой (7. 77) из раздела 7. 1 " Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях " модуль p_imвектора p _im магнитного момент одной молекулы в магнетике, а произведение I_i_мол'nS_мол - модульвектора магнитногомомента единицы объёма магнетика, т. е. согласно (7. 45) - это модульJ вектора J намагниченности.

Поэтому с учётом равенства модуляJ вектора J намагниченности I_i_мол'nS_мол, т. е. J = I_i_мол'nS_мол, выражение (7. 112) принимает следующий вид: I_мол_V = Jdlcosα , (7. 113) где α - это (рис. 7. 26) угол между вектором J намагниченности материала магнетика и малым dl элементом воображаемого Г контура, находящимся в OYZ плоскости и разделяющим верхнюю часть этого магнетика от нижней части.

Введя вектор d l , направленный по (рис. 7. 26) оси воображаемого косого цилиндра, преобразуем (7. 113) в следующее скалярное произведение: I_мол_V = J d l , (7. 114) где I_мол_V - суммарныймолекулярный ток, пересекающий V объём косого цилиндра элементарной

dl длиной, или суммарный молекулярный ток, " нанизанный" на элементарную dl длину воображаемого Г контура.

Результирующий молекулярный ток I_молсилой в магнетике через поверхность S площадью (рис. 7. 26), которую охватывает воображаемый Г контур и включающий все малые dl элементы этого воображаемого Г контура, с учётом (7. 108) и (7. 114) имеет следующий вид:

I_мол = ∫ j _мол d S = ∫ J d l , (7. 115) S Г

где (7. 115) является выражением, связывающим молекулярные токи в магнетике с намагниченностью в интегральном виде.

Связь молекулярных токов в магнетике с намагниченностью в дифференциальном виде

Перейдя в(7. 115) с использованием теоремы Стоксаот интеграла по Г контуру к поверхностному интегралу по поверхности S площадью, " натянутой" на этот Г контур, получим следующее выражение: ∫ j_мол d S = ∫ J d l = ∫ [ J] d S ↔ j_мол = [ J]. (7. 116) S Г S

где (7. 116) является выражением, связывающим молекулярные токи в магнетике с намагниченностью в дифференциальном виде.

Вектор j _мол плотности молекулярных токов определяется значением ротора [J] вектора J намагниченности в магнетике. По аналогии с (5. 42) из раздела 5. 1 « Электрическое поле системы неподвижных зарядов в вакууме. Теорема Гаусса для электростатического поля. Работа и потенциал электростатического поля» ротор J вектора, т. е. rotJ намагниченности в магнетике для случая представления векторного поля в прямоугольной декартовой системе (1. 1) из раздела 1. 0 " Физические основы механики" координат определяется следующим выражением: i j k

j _мол= [ J]    = rotJ =    ∂ /∂ x ∂ /∂ y ∂ /∂ z = [(∂ J_z /∂ y) - (∂ J_y /∂ z)] i + [(∂ J_x/∂ z) - (∂ J_z/∂ x)] j +                                                                J_xJ_yJ_z

                                          + [(∂ J_y /∂ x) - (∂ J_x /∂ y)] k. (7. 117)       В случае, когда в произвольной точке пространства, занятого магнетиком, rotJ = 0, то в этой произвольной точке пространства плоскости вращения S_мол молекулярных I_i_мол токов единичных молекул ориентированы так, что вектор j _мол результирующей плотности молекулярных токов в произвольной точке пространства равна нулю.

       В произвольных точках пространства, занятого магнетиком, где rotJ ≠ 0, оказывается отличной от нуля и вектор j _мол плотности молекулярных токов тоже отличен от нуля, причём векторы rotJ и j _мол плотности молекулярных токов имеют одинаковое направление.



       Вектор напряженности магнитного поля и его связь с векторами индукции                                                           и намагниченности

       Подставим (7. 116) выражение связи вектора j _мол плотности молекулярных токов с ротором

[J] вектора J намагниченности в (7. 107) выражение связи ротора [ B] результирующего вектора B индукции магнитного поля в произвольной точке пространства, занятого магнетиком, с суммой векторов плотностей j макроскопического и j_мол молекулярного токов, после чего получим следующее выражение связи ротора [ B/ μ ₀ ] этого результирующего вектора B индукции магнитного поля в произвольной точке пространства, занятого магнетиком, с вектором j плотностимакроскопического тока:         [   B ] = μ ₀( j + j_мол )= μ ₀ j + μ ₀ [ J] ↔ [  , B/ μ ₀ ] = j + [ J]. (7. 118)    Объединим в (7. 118) роторы и получим следующее выражение связи вектора j плотностимакроскопического тока в произвольной точке пространства, занятого магнетиком, с векторами     B индукции магнитного поля и J намагниченности в этой произвольной точке пространства:                                                                                                                          [  , [( B/ μ ₀)- J ] ] = j, (7. 119) где j - вектор плотности макроскопического или тока проводимости в произвольной точке пространства.

       Введём следующее выражение вектора H напряжённости магнитного поля в произвольной точке пространства, занятого магнетиком, в (7. 119) соотношение:                  ( B/ μ ₀)- J = H. (7. 120)       Подставим (7. 120) в (7. 119) и получим следующее выражение связи вектора j плотностимакроскопического тока в произвольной точке пространства с вектором H напряжённости магнитного поля в этой произвольной точке, занятого магнетиком:

12 3 4 5 6 7 8 Следующая ⇒