Главная

Контакты

Случайная статья

• Автоматизация
• Антропология
• Археология
• Архитектура
• Биология
• Ботаника
• Бухгалтерия
• Военная наука
• Генетика
• География
• Геология
• Демография
• Деревообработка
• Журналистика
• Зоология
• Изобретательство
• Информатика
• Искусство
• История
• Кинематография
• Компьютеризация
• Косметика
• Кулинария
• Культура
• Лексикология
• Лингвистика
• Литература
• Логика
• Маркетинг
• Математика
• Материаловедение
• Медицина
• Менеджмент
• Металлургия
• Метрология
• Механика
• Музыка
• Науковедение
• Образование
• Охрана Труда
• Педагогика
• Полиграфия
• Политология
• Право
• Предпринимательство
• Приборостроение
• Программирование
• Производство
• Промышленность
• Психология
• Радиосвязь
• Религия
• Риторика
• Социология
• Спорт
• Стандартизация
• Статистика
• Строительство
• Технологии
• Торговля
• Транспорт
• Фармакология
• Физика
• Физиология
• Философия
• Финансы
• Химия
• Хозяйство
• Черчение
• Экология
• Экономика
• Электроника
• Электротехника
• Энергетика

B1nсоставляющейи вектором B1 индукции магнитного поля в среде магнетикаμ1 магнитной проницаемостью, а также  α2 угол  между нормальной B2nсоставляющейи вектором 3 страница

где для рис. 7. 29 μ ₂ > μ ₁.

Магнитное поле проводника с током в вакууме и при заполнении пространства, окружающего его, однородным непроводящим магнетиком

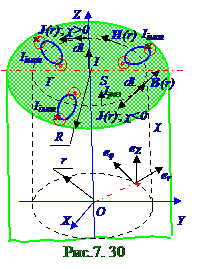
       В магнитном поле проводника с током в вакууме векторы B (r) индукции   (7. 6) из раздела 7. 1 " Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях ", H (r) напряжённости  (7. 120), намагниченности J (r) (7. 126) магнитного поля представляют собой цилиндрическое векторное поле, поскольку все эти векторы (рис. 7. 30) находятся на окружностях, соосных с цилиндрическим проводником из магнетика с χ магнитной восприимчивостью, и направлены по касательной к этой окружности, т. е. коллинеарны e_φ орту цилиндрической системы  координат.

       Циркуляция  (7. 122) вектора H (r) напряжённости магнитного поля в интегральном виде по воображаемой окружности (рис. 7. 30) радиусом rв области пространства, занятого магнетиком, равна  результирующему I_рез макроскопическому или току проводимости через поверхность  S площадью, которую охватывает эта окружность r радиусом. Охватываемая воображаемой окружностью  r радиусом поверхность - это круг r радиусом от поперечного сечения цилиндрического проводника, перпендикулярного его оси. По нормали к поверхности этого круга (рис. 7. 30)течётток проводимости с j А/м² модулём    jвектора плотности, который имеет следующий вид:                                                                                                                                                           j = I/π R² А/м².    (7. 135)

                                                                              ∫ H d l = H_l2π r = I_рез ↔ H_l = I_рез/2π r↔ H = I_рез/2π r, (7. 137)                                                                        Г

где (рис. 7. 30) 0 ≤ r ≤ R.

       Поперечное сечение цилиндрического проводникаиз магнетика c χ магнитной восприимчивостью (рис. 7. 30) перпендикулярно его оси, поэтому вектор d l обхода Г контура r радиусом тоже перпендикулярен оси цилиндрического проводника и сонаправлен e_φ орту в цилиндрической системе  координат. С учётом сонаправленности e_φ орта вектору d l обхода Г контура r радиусом          H_l проекция навектор d l обхода Г контураравна H _φ проекции вектора H напряжённости магнитного поляна e_φ орт, т. е. H_l = H _φ и она положительна при положительном направлении обхода Г контура r радиусом  против " часовой стрелки" и направлении результирующего I_рез макроскопического или тока проводимости по OZ оси, поэтомус учётом равенства нулю проекций    H _r, H _Z вектора H напряжённости магнитного поляна соответственно e_r, e_Z орты в цилиндрической системе  координат эта H_l проекция равна H модулю (7. 137) вектора H напряжённости магнитного поля.

       Вектор J намагниченности J (7. 126) магнетика, из которой изготовлен цилиндрический проводник, имеет следующий вид:                                                                      J = χ H,       (7. 138)

где вектор J намагниченности магнетика (рис. 7. 30) сонаправлен вектору H напряжённости магнитного поля (7. 138)в магнетике цилиндрического проводника, когда χ > 0 для парамагнетиков и ферромагнетиков, и вектор J намагниченности противонаправлен вектору H напряжённости магнитного поля   в магнетике цилиндрического проводника, когда χ < 0 для диамагнетиков.                          Подставляем магнитную χ восприимчивость магнетика, из которой изготовлен цилиндрический проводник, а также  H_l проекцию наd l вектор, которая равна H модулю (7. 138) вектора H напряжённости магнитного поля, в (7. 137), и получаем следующее выражение для                         J _l(r) проекции навектор d l обхода Г контура вектора J намагниченности магнетика, из которой изготовленэтот цилиндрический проводник, в функции от r радиуса (рис. 7. 30) окружности, охватывающей круговую поверхность магнетика S площадью:        J _l = χ H = χ rI/2π R² А/м, (7. 139)

где (рис. 7. 30) 0 ≤ r ≤ R.

       Проекция J _l(r) навектор d l обхода Г контура (7. 137) вектора J намагниченности магнетика (рис. 7. 30), в функции от r радиуса   окружности, охватывающей круговую поверхность магнетика     S площадью, является положительной величиной, когда    χ > 0 для парамагнетиков и ферромагнетиков, и является отрицательной величиной, когда χ < 0 для диамагнетиков.

       Проекция J _l(r) навектор d l обхода Г контура вектора J намагниченности магнетика (рис. 7. 30) на круговой поверхности магнетика сr = R радиусом с учётом(7. 139) имеет следующий вид:                                                                                                                                  J _{l|r = R} = χ I/2π R  А/м.    (7. 140)        Вектор J (r) намагниченности   магнетика (рис. 7. 30) коллинеарен e_φ орту цилиндрической системы  координат, поэтому векторное выражение (7. 138) имеет следующий вид:                                                                                                                                  J = χ H = e_φ χ rI/2π R² А/м, (7. 141)

где (рис. 7. 30) 0 ≤ r ≤ R и вектор J (r) намагниченности магнетика сонаправлен вектору                     H напряжённости магнитного поля, если χ > 0 для парамагнетиков и ферромагнетиков, и противонаправлен вектору H напряжённости магнитного поля   в магнетике цилиндрического проводника, когда χ < 0 для диамагнетиков.                                                                                       

       Ротация вектора J (r) намагниченности   (7. 141)   магнетика с учётом равенства нулю проекций J_r, J_Z этого вектора на соответственно e_r, e_Z орты в цилиндрической системе координат и отличия от нуля проекцииJ _φ (r) на e_φ орт, а также с учётом зависимости этой проекции J _φ только от          r модуля r радиуса-вектора, направленного по орту e_r, и равенства проекцииJ _φ (r) на e_φ орт проекции    J _l(r) на   вектор d l обхода Г контура  вектора J намагниченности магнетика (рис. 7. 30), т. е. J _φ (r)= J_l(r) приводит к следующему выражению вектора j_мол плотности  молекулярных токов (7. 116), равным значению ротора намагниченности [J] в произвольной точке пространства, зависящей в цилиндрической системе координат только от r модуля r радиуса-вектора:

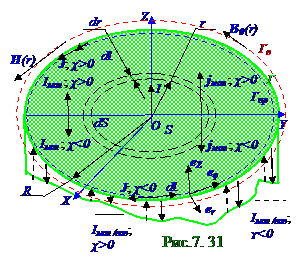
                                                                                j_мол = [ J] ={(1/r)[∂ (rJ _φ )/∂ r]} e_Z = e_Z χ I/π R², (7. 142) где (рис. 7. 31) 0 ≤ r ≤ R.  

       Вектор j_мол плотности  молекулярных токов магнетика направлен (рис. 7. 31) по e_Z орту в цилиндрической системе координат, т. е. в одну сторону с результирующей током I силой проводимости в магнетике цилиндрического проводника, если χ > 0 для парамагнетиков и ферромагнетиков, а, если χ < 0 для диамагнетиков, то вектор j _мол плотности  молекулярных токов магнетика направлен противоположно e_Z орту в цилиндрической системе координат, т. е. в противоположную сторону с результирующей током I силой проводимости в магнетике цилиндрического проводника.                                                                                 

       Проекция j_молZ на e_Z орт в цилиндрической системе  координат (рис. 7. 31) вектора                      j_мол плотности   молекулярных токов имеет следующий вид с учётом её (7. 142) постоянной величины в пределах поперечного сечения круга R радиусом магнетика цилиндрического проводника:                                                                                                                                          j_молZ = χ I/π R²,    (7. 143)

где (рис. 7. 31) 0 ≤ r ≤ R.

       Проекция j_молZ является положительной величиной, если χ > 0 для парамагнетиков и ферромагнетиков, а, если χ < 0 для диамагнетиков, то проекция j_молZ является отрицательной величиной.

       Молекулярный  ток dI_мол силой (7. 108) ток, текущий через кольцо с элементарной (рис. 7. 31)  толщиной dr  и r радиусом, который находится в интервале 0 ≤ r ≤ R значений, с учётом её (7. 143) имеет следующий вид:                                             dI_мол = j_молZ 2π rdr = (χ I/π R²)2π rdr = χ 2Irdr/R², (7. 144)      

где dS = 2π rdr - площадь элементарного кольца в поперечном сечении цилиндрического проводника, перпендикулярного его оси; перпендикулярно поверхностиэтого элементарного кольца течёт молекулярный ток dI_мол силой.

       Молекулярный  I_молток, текущий (рис. 7. 31) через поперечное сечение круга R радиусом магнетика цилиндрического проводника, перпендикулярного его оси, с учётом (7. 143), согласно (7. 104), имеет следующий вид:                                              R                     R                                                                                                        I_мол = ∫ j_мол d S = ∫ dI_мол = (χ 2I/R²) ∫ rdr = χ I А,    (7. 145)  

                                                                            S        0                  0

где молекулярный  I_молток направлен по e_Z орту в цилиндрической системе координат, т. е. в одну сторону стоком Iсилой проводимости в магнетике цилиндрического проводника, если χ > 0 для парамагнетиков и ферромагнетиков, а, если χ < 0 для диамагнетиков, то молекулярный I_мол результирующий  токнаправлен противоположно e_Z орту в цилиндрической системе координат, т. е. в противоположную сторону стоком Iсилой проводимости в магнетике цилиндрического проводника.

       Молекулярный  ток I_мол силой согласно   (7. 115) определяется  циркуляцией    вектора J _пр намагниченности   по воображаемой окружности (рис. 7. 31) r= R радиусом Г_пр контуру c внутренней стороны поперечного сечения цилиндрического проводникаиз магнетика c  χ _пр магнитной восприимчивостью, перпендикулярного его оси. С учётом (7. 139) проекции J_{пр l} навектор d l обхода     Г_пр контура вектора J _пр намагниченности магнетика (рис. 7. 31) на круговой поверхности магнетика сr = R радиусом, т. е. Г_пр контуре, который охватывает поперечное сечение магнетика этого цилиндрического проводника, молекулярный  ток I_мол силой, текущий  через поперечное сечение магнетика R радиусомS = π R² площадью цилиндрического проводника, перпендикулярное его оси, имеет следующий вид:

                                                      I_мол =   ∫ J _прd l = ∫ J _{пр|r =R} d l  = J_{прl|r = R}2π R  =  (χ I/2π R) 2π R =  χ I А, (7. 146)                                                                      Г_пр    Г_{пр|r = R}

где молекулярный  I_мол результирующий  (рис. 7. 31) ток направлен по e_Z орту в цилиндрической системе координат в одну сторону стоком Iсилой проводимости в магнетике цилиндрического проводника, если    χ > 0 для парамагнетиков и ферромагнетиков, т. е. когда J _пр вектор намагниченности  сонаправлен вектору d l обхода  Г_пр контура R радиусом и поэтому J_прl проекция этого вектора J _пр намагниченности навектор d l обхода Г_пр контура является положительной величиной; молекулярный  I_мол результирующий  (рис. 7. 31) ток направлен противоположно e_Z орту в цилиндрической системе координат и току Iсилой проводимости в магнетике цилиндрического проводника, если χ < 0 для диамагнетиков, т. е. когда вектор J _пр намагниченности  противонаправлен вектору d l обхода Г_пр контура R радиусом и поэтому J_прl проекция этого вектора J _пр намагниченности навектор d l обхода Г_пр контура является отрицательной величиной.

       Равенство  (7. 145) и  (7. 146) соответствует следующему выражению (7. 115):                                                                                                                                                   I_мол = ∫ j_мол d S = ∫ J d l , (7. 147)                                                                                                                            S            Г

что является подтверждением правильности расчётов в данном выводе.

       Циркуляция  (7. 146) вектора J _в(r) намагниченности   (7. 141)  магнитного поля по воображаемой окружности - (рис. 7. 31) Г_в контуру R радиусом c внешней стороны поперечного сечения   (рис. 7. 31) магнетика цилиндрического проводника, перпендикулярного его оси, равна следующей сумме молекулярных токов I_мол;   I_{мол. пов.} силой, соответственно текущих перпендикулярно поверхности  S площадью этого поперечного сечения и по боковой поверхности цилиндрического проводникаиз магнетика:

где (7. 148) приравнено нулю, п. ч. Г_в контур R радиусом c внешней стороны поперечного сечения цилиндрического проводникаиз магнетика проходит в вакууме, где вектор J _в(r) намагниченности равен нулю.               

которую охватывает эта окружность r радиусом:  ∫ H d l = H_l2π r = I ↔ H_l = I/2π r↔ H = I/2π r,     (7. 149)                                                                              Г_м

где (рис. 7. 32) 0 ≤ r ≤ R; I - сила макроскопического или тока проводимости, текущего перпендикулярно поверхности  S = π R² площадью, которая представляет собой поперечное сечение цилиндрического проводникаиз магнетика с χ _пр магнитной восприимчивостью.

       Поперечное сечение цилиндрического проводникаиз магнетика c χ _пр магнитной восприимчивостью (рис. 7. 32) перпендикулярно его оси, поэтому вектор d l обхода Г_м контура c внешней стороны этого поперечного сечения тоже перпендикулярен оси цилиндрического проводника и сонаправлен e_φ орту в цилиндрической системе  координат. С учётом сонаправленности e_φ орта вектору d l обхода Г_м контура c внешней стороны поперечного сечения цилиндрического проводникаH_l проекция наd l вектор равна H _φ проекции вектора H напряжённости магнитного поляна e_φ орт, т. е. H_l = H _φ , и она является положительной величиной при положительном направлении обхода Г_м контура R радиусом против " часовой стрелки" и направлении                              I макроскопического или тока проводимости по OZ оси. Поэтомус учётом равенства нулю проекций   H _r, H _Z вектора H напряжённости магнитного поляна соответственно   e_r, e_Z орты в цилиндрической системе  координат эта H_l проекция равна H модулю (7. 138) вектора  H напряжённости магнитного поляна Г_м контуре R радиусом.

где (рис. 7. 32) r ≤ R; I - сила макроскопического или тока проводимости, текущего перпендикулярно поверхности  S = π R² площадью, которая представляет собой поперечное сечение цилиндрического проводникаиз магнетика с χ _пр магнитной восприимчивостью, перпендикулярное его оси.

    Вектор j _мол плотности  молекулярных токов в непроводящем магнетике с                             χ _м восприимчивостью, окружающем цилиндрический проводник с χ _пр магнитной восприимчивостью, по аналогии с (7. 142) имеет с учётом (7. 150) следующий вид: