B1nсоставляющейи вектором B1 индукции магнитного поля в среде магнетикаμ1 магнитной проницаемостью, а также α2 угол между нормальной B2nсоставляющейи вектором 4 страница

j_мол= [J] = {(1/r)[∂ (rJ_м _l)/∂ r]} e_Z = (1/r)[∂ (rχ _мI/2π r)/∂ r] e_Z = (1/r)[∂ (χ _мI/2π )/∂ r] e_Z = 0, (7. 151)

т. е. молекулярный токв непроводящем магнетике χ _м восприимчивостью, окружающем цилиндрический проводник с χ _пр магнитной восприимчивостью, отсутствует.

Циркуляция (7. 146) вектора J _м намагниченности в непроводящем магнетике с χ _м магнитной восприимчивостью по воображаемой окружности (рис. 7. 32) r= R радиусом Г_м контуру c внешней стороны поперечного сечения цилиндрического проводникаиз магнетика c χ _пр магнитной восприимчивостью, перпендикулярного его оси, имеет с учётом (7. 149) следующий вид:

∫ J _м d l = ∫ J _м_|_r ₌_R d l = J_м_l_|_r ₌_R2π R = (χ _м RI/2π R²)2π R = χ _мI А, (7. 152) Г_м Г_м_|_r ₌_R

где I - сила макроскопического или тока проводимости, текущего перпендикулярно поверхности S = π R² площадью, которая представляет собой поперечное сечение, перпендикулярное оси цилиндрического проводникаиз магнетика с χ _пр магнитной восприимчивостью; J_м_l_|_r ₌_R - проекция навектор d l обхода Г_м контура вектора J _м намагниченности в непроводящем магнетике с χ _м магнитной восприимчивостью, который охватывает c внешней стороны поперечное сечение цилиндрического проводника c χ _пр магнитной восприимчивостью, перпендикулярное его оси, вследствие чего длина этого Г_м контура r= R радиусом равна 2π R длине окружности.

Циркуляция (7. 152) вектора J _м(r); намагниченности в непроводящем магнетике с χ _м магнитной восприимчивостью по воображаемой окружности (рис. 7. 32) r= R радиусом Г_м контуру c внешней стороны поперечного сечения цилиндрического проводникаиз магнетика c χ _пр магнитной восприимчивостью, перпендикулярного его оси (7. 150), равна с учётом (7. 152) следующей сумме охватываемых этим Г_м контуром: молекулярного тока I_мол = χ _прI силой(7. 146), которыйтечёт через поперечное сечение, перпендикулярное оси цилиндрического проводника c χ _пр магнитной восприимчивостью, R радиусоми S = π R² площадью, и молекулярного поверхностного тока_.I_{мол. пов}_.силой, которыйтечёт по поверхности раздела цилиндрического проводника c χ _пр магнитной

о_м

восприимчивостьюи

непроводящего магнетика с χ _м магнитной восприимчивостью, окружающегоэтот цилиндрический проводник:

∫ J _м_|_r ₌_R d l = I_мол + I_{мол. пов} ↔ I_{мол. пов} = ∫ J _м_|_r ₌_R d l - I_мол ↔ I_{мол. пов} = χ _мI - χ _прI = I(χ _м - χ _пр) А, (7. 153) Г_м_|_r ₌_R Г_м_|_r ₌_R

Согласно(7. 153) поверхностный ток_.I_{мол. пов}_.силой, которыйтечёт по поверхности раздела цилиндрического проводника c χ _пр магнитной восприимчивостьюи непроводящего магнетика с χ _м магнитной восприимчивостью, окружающегоэтот цилиндрический проводник, направлен (рис. 7. 32) в одну сторону с макроскопическим или током проводимости (7. 137) I силой, если χ _м - χ _пр> 0. При χ _м - χ _пр< 0 поверхностный ток_.I_{мол. пов}_.силой течёт в противоположном направлении с макроскопическим или током проводимости I силой. При этом χ _м > 0 и χ _пр > 0 для парамагнетиков и ферромагнетиков; χ _м < 0 и χ _пр < 0 для диамагнетиков.

Согласно(7. 153) молекулярный результирующий ток I_мол силой, текущий через поперечное сечение магнетика R радиусом S = π R² площадью цилиндрического проводника, перпендикулярное его оси, определяется циркуляцией вектора J _пр(r) намагниченности по воображаемой окружности (рис. 7. 32) r= R радиусом Г_пр контуру c внутренней стороны поперечного сечения цилиндрического проводникаиз магнетика c χ _пр магнитной восприимчивостью и имеет следующий вид: I_мол = ∫ J _прd l = ∫ J _пр_|_r ₌_R d l = J_пр_l_|_r ₌_R 2π R, (7. 154) Г_пр Г_пр_|_r ₌_R

где J_пр_l_|_r ₌_R - проекция навектор d l обхода Г_пр контура вектора J _пр намагниченности, который охватывает c внутренней стороны поперечное сечение цилиндрического проводника c χ _пр магнитной восприимчивостью, перпендикулярное его оси, вследствие чего длина этого Г_пр контура r= R радиусом равна 2π R длине окружности.

Подставляем (7. 153) в (7. 154) и получаем следующее выражение j_{мол. пов}_Zпроекциина e_Z орт в цилиндрической системе координатвектораj_{мол. пов}плотности поверхностноготока_., которыйтечёт по поверхности раздела цилиндрическогопроводника c χ _пр магнитной восприимчивостьюинепроводящего магнетика с χ _м магнитной восприимчивостью, окружающегоэтотцилиндрическийпроводник: I_мол_._пов = ∫ J_м_|r_=Rdl - I_мол ↔ I_мол_._пов = ∫ J_м_|r_=Rdl - Г_м_|r_{= R} Г_м_|r_{= R} - ∫ J_пр_|r_=Rdl = J_м_l|r_{= R}2π R -- J_пр_l|r_=R2π R ↔ Г_пр_|r_{= R} ↔ I_мол_._пов/2π R = J_м_l|r_{= R}- J_пр_l|r_=R↔ ↔ j_мол_._пов_Z= J_м_l- J_пр_l, (7. 155) где j_{мол. пов}_Z - проекцияна e_Z орт в цилиндрической системе координат вектора

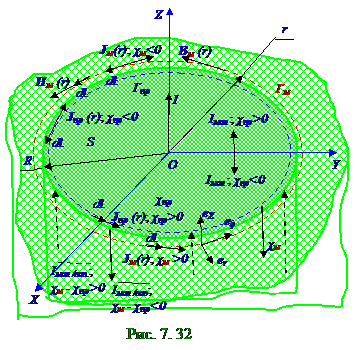
j _{мол. пов} плотности поверхностного тока_., которыйтечёт по направлению e_Z орта в цилиндрической системе координат, т. е. (рис. 7. 32) по направлению I макроскопического или тока проводимости, если разность J_м_l_|_r ₌_R проекции навектор d l обхода Г_м контура вектора J _м намагниченности в непроводящем магнетике с χ _м магнитной восприимчивостью и J_пр_l_|_r ₌_R проекции навектор d l обхода Г_пр контура вектора J _пр намагниченности в магнетике с χ _пр магнитной восприимчивостью является положительной величиной, т. е. если J_м_l - J_пр_l > 0; если J_м_l - J_пр_l < 0, то j_{мол. пов}_Z проекция на e_Z орт в цилиндрической системе координат вектора j _{мол. пов} плотности поверхностного тока является отрицательной величиной_.и поверхностный ток течёт противоположно направлению e_Z орта в цилиндрической системе координат, т. е. (рис. 7. 32) противоположно направлению I макроскопического или тока проводимости.

Модуль j_{мол. пов} вектора j _{мол. пов} плотности поверхностного токаимеет размерность А/м и численно равен силе тока, протекающего (рис. 7. 32) перпендикулярно Г_пр, Г_м контурамчерез единицу длины этих контуров.

Модуль B(r) вектора B (r)индукции магнитного поля (7. 127) в произвольной точке пространства, занятого магнетиком (рис. 7. 32)с μ _м магнитной проницаемостью, окружающего цилиндрический проводник, в котором модуль H(r) вектора H (r) напряжённости магнитного поля определяется (7. 139), имеет следующий вид: B= μ ₀ μ _мI_рез/2π r = μ _мB₀, (7. 156)

где B₀ - модуль вектора B ₀(r)индукции магнитного поля в вакууме (рис. 7. 31)с магнитной μ _в проницаемостью, окружающего цилиндрический проводник, равной единице, т. е. μ _в=1.

Физическая природа диамагнетизма

Вектор (7. 77) из раздела 7. 1 " Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях " магнитного p _m момента плоского Г контура с круговым током I_крсилы, который создаёт -e электрон (рис. 7. 33), вращающийся по окружности r радиусом с вектором v скорости вокруг ядра атома имеет следующий вид:

p _m = IS n ↔ p_m = IS = enπ r²= e(v/2π r)π r²= evr/2, (7. 157) где n - единичный вектор, нормальный к поверхности S площади круга,

ограниченной окружностью, по которой двигается -e электрон, и направленный так, что из концаэтого n единичного вектора вращение -e электрона видно " по часовой стрелке" ; n = v/2π r - число оборотовв единицу времени или частота вращения(1. 20)из раздела 1. 0 " Физические основы механики" -e электрона, движущегося с (рис. 1. 9) из раздела 1. 0 " Физические основы механики" модулем vвектора v линейной " натянута" плоская поверхность S площадью, в этом случае имеет следующий вид: p_m = ISn ↔ p_m = IS, (7. 45) где p_m - модуль вектора p_m магнитного момента Г контура с током I силой, на который " натянута" поверхность S площадью

скорости по окружности 2π r длиной; I = en - величина Δ q заряда, переносимая через площадку в любом месте на пути движения электронаего e элементарным зарядом запромежуток Δ t времени, равный единице t времени, что делает возможным (6. 3) из раздела 6. 0 " Электрический ток" величину en считать круговым током I_крсилы; S = π r² - площадь круга, ограниченная окружностью, по которой двигается электрон; p_m - модуль вектора p_m магнитного момента, создаваемого вращающимся -e электроном, вследствие чего этот вектор p_m магнитного момента называют орбитальным магнитным моментом -e электрона.

Орбитальный p_m магнитный момент (рис. 7. 33) -e электрона образует с направлением вращения этого электрона левовинтовую систему, а (1. 68) из раздела 1. 0 " Физические основы механики" вектор L момента импульса -e электрона m массой относительно O начала координат образует с направлением вращения этого -e электрона правовинтовую систему и имеет следующий вид: L = [ r, m v], (7. 158) где r , v - соответственно радиус - вектор и вектор скорости -e электрона. Поэтому вектор

L момент импульса, называемый орбитальным механическим моментом -e электрона, и

p_m орбитальный магнитный момент -e электронанаправлены (рис. 7. 33) в противоположные стороны.

Отношение проекций p_mz , L_zна OZ ось векторов орбитальных соответственно(7. 157)

p _m магнитного, (7. 158) L механического моментов -e электрона называют магнитомеханическим или гиромагнитным отношением, которое имеет следующий вид: p_mz /L_z = (evr/2)/ -rmv = - e/2m, (7. 159) где L_z = -rmv - проекция на OZ ось вектора (рис. 7. 33) орбитального (7. 126) L механического момента -e электронаимеет знак " -" , потому что этот вектор орбитального L механического момента -e электрона направлен противоположно OZ оси.

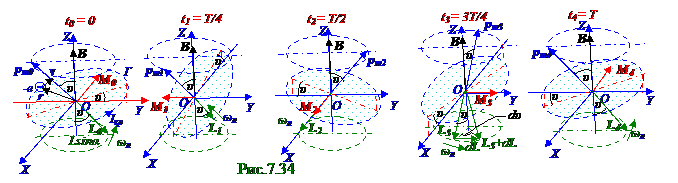
Вектор (7. 82)из раздела 7. 1 " Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях " M = [ p_m, B] момента силы, действующего на контур с вектором p _m орбитального магнитного момента, который создаёт -e электрон (рис. 7. 33), вращающийся по окружности r радиусом с вектором v скорости, направлен (рис. 7. 34) перпендикулярно плоскости, образованной этим вектором p _m магнитного момента и вектором B индукциимагнитного поля в магнетике, вследствие чего модуль M вектора M момента силы имеет следующий вид: M = p_mBsinυ , (7. 160)

где υ - угол между векторами p _m и B; p_m, B - модули орбитальных векторов соответственно

⇐ Предыдущая 1 2 345 6 7 8 Следующая ⇒