Хелпикс

Главная

Контакты

Случайная статья



ДОМАШНЄ ЗАВДАННЯ. ЛІТЕРАТУРА. ПРАКТИЧНЕ ЗАНЯТТЯ №11

⇐ ПредыдущаяСтр 11 из 11


ДОМАШНЄ ЗАВДАННЯ

1. Довести, що множина 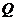 всіх квадратних матриць над полем дійсних чисел – комутативне кільце.

 

2. Довести, що множина К всіх чисел виду 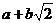, де a і b – раціональні числа, є полем.

 

3. Робота з індивідуальним завданням.

 

ЛІТЕРАТУРА

 

1. Завало С. Т., Костарчук В. М., Харцет В. І. Алгебра і теорія чисел. Частина 1. – К.: Вища школа, 1971. – С. 180-215.

2. Завало С. Т., Костарчук В. М., Харцет В. І. Алгебра і теорія чисел. Частина 2. – К.: Вища школа, 1971. – С. 162-182.

 


ДИСКРЕТНА МАТЕМАТИКА”

ПРАКТИЧНЕ ЗАНЯТТЯ №11

 

Тема. “КОМБІНАТОРИКА”.

 

            ПЛАН

1. Основні правила комбінаторики.

2. Розміщення, перестановки, комбінації.

3. Розміщення, перестановки, комбінації з повторенням.

 

 

 

Завдання 1. У квітковій крамниці є 10 видів квітів, 6 видів оздоблювальних рослин і 8 видів упаковки. Кільки різних букетів можна скласти з однієї кітки, однієї оздоблювальної рослини і одного виду упаковки?

 

Завдання 2. Скільки треба мати словників, щоб можна було робити переклади з кожної з 5 мов на будь-яку іншу?.

Завдання 3. Одного разу 10 друзів зайшли до ресторану. Господар запропонував їм приходити до нього щодня і безкоштовно обідати, якщо кожного разу вони сідатимуть за той самий стіл по-іншому. Коли настане день, у який за обід друзям доведеться заплатити?

 

Завдання 4. Скільки перестановок можна зробити з літер слова “міссісіпі”?

 

Завдання 5. Скільки діагоналей у правильному п-кутнику?

Завдання 6. Скільки натуральних дільників має число 2310=2*3*5*7*11?

Завдання 7. Скільки натуральних дільників має число 2310=2*3*5*7*11?

Завдання 8. У кондитерський відділ завезли тістечка чотирьох видів. Скількома способами можна купити 7 тістечок?

 

Завдання 9. У комп¢ ютерному центрі працюють 67 осіб. З них 47 знають мову програмування Pascal, 35 осіб – С++, 23 – обидві з цих мов. Скільки осіб не знають жодної мови?

 

 

 

ДОМАШНЄ ЗАВДАННЯ

  1. Робота з індивідуальним завданням.

 

ЛІТЕРАТУРА

 

1. Виленкин Н. Я. Комбинаторика. – М.: Наука, 1969. – 328 с.

2. Сачков В. Н. Введение в комбинаторные методы дискретной математики. – М.: Наука, 1982, – 384 с.


⇐ Предыдущая234567891011
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.