Таблиця міток LABLE. Вершини. Таблиця міток PRED. ДОМАШНЄ ЗАВДАННЯ. ЛІТЕРАТУРА. ПРАКТИЧНЕ ЗАНЯТТЯ №9

Таблиця міток LABLE

Крок і	Вершини
Крок і	A	B	C	D	E	F	G	H
	0*	¥	¥	¥	¥	¥	¥	¥
			¥		¥	¥	1*	¥
			¥	6*	¥	¥		¥
		7*	¥			¥
			¥		14*	¥
			¥		14*	¥		19*
			¥			23*
			¥ *

Таблиця міток PRED

PRED (A)	A
PRED (B)	A
PRED (C)	C
PRED (D)	G
PRED (E)	D
PRED (F)	H
PRED (G)	A
PRED (H)	D

Таблиця найкоротших шляхів

Від	До	Найкоротший шлях
A	B	A, B
A	C	Немає шляху
A	D	A, G, D
A	E	A, G, D, E
A	F	A, G, D, H, F
A	G	A, G
A	H	A, G, D, H

ДОМАШНЄ ЗАВДАННЯ

У заданому графі визначити шлях з найменшою кількістю дуг.

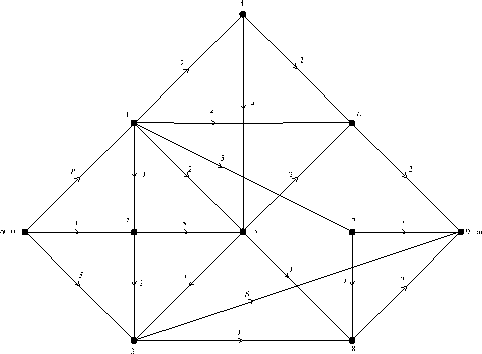
Визначити найкоротший шлях з вершини А до вершини L заданого графа.

Робота з індивідуальним завданням.

ЛІТЕРАТУРА

Басакер Р., Саати Т. Конечные графы и сети. – М.: Наука, 1974. – С. 179-182.
Белов В. В., Воробьев Е. М., Шаталов В. Е. Теория графов. – М.: Высшая школа, 1976. – С. 20-22, 114-128.
Свами М., Тхуласираман К. Графы, сети и алгоритмы. – М.: Мир, 1984. – С. 361-376, 380-418.
Федосеева Л. И. Дискретная математика: Учеб. -практич. пособие. – Пенза: Изд-во Пенз. технол. ин-та, 1998. – С. 75-98.

ДИСКРЕТНА МАТЕМАТИКА”

ПРАКТИЧНЕ ЗАНЯТТЯ №9

Тема. “МАКСИМАЛЬНІ ПОТОКИ”.

ПЛАН

Транспортна мережа.
Потоки у транспортній мережі. Максимальний потік.
Алгоритм Форда і Фалкерсона.

Завдання 1. Використовуючи алгоритм Форда і Фалкерсона, знайти максимальний потік у заданій транспортній мережі, зображеній на рисунку. На цьомурисунку поруч з кожним ребром 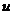показані значення 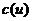і 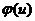відповідно (через кому). У якості початкового потоку за алгоритмом припускаємо, що всі .

Шлях 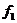: 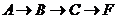. Помітимо вершини у такому порядку:

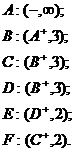
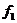Всі ребра є прямими. Тому для отримання зміненого потоку збільшуємо потоки всіх ребер шляху на .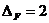

Мітки всіх вершин витираємо. Доповнюючий шлях до 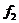є таким:

Шлях 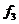: 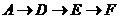. Вершини отримають мітки:

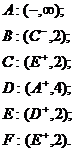
Всі ребра є прямими. Тому для отримання зміненого потоку збільшуємо потоки всіх ребер шляху 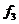на .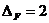

Доповнюючий шлях 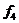до 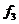складається з вершин: . Ребро, що з’єднує вершини С і В є оберненим у цьому шляху. Всі інші ребра – прямими. Тому використовуватимо обернене помічування:

Збільшуємо потоки у прямих ребрахна 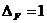і на стільки ж зменшуємо потік в оберененому ребрі:

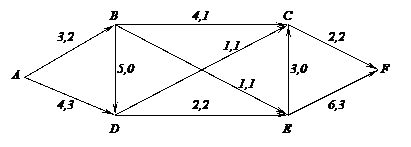Надамо нові мітки вершинам:

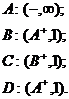
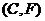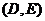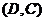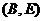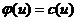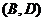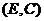Далі помітити інші вершини неможливо, бо у ребрах , , і величина потоку дорівнює пропускній здатності дуги ( . Тому порушується можливість прямого помічування. У дугах і величина потоку , тому порушується можливість оберненого помічування.

Отже, доповнюючого потоку не існує. Тому отриманий потік 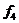– максимальний.

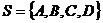. Розріз 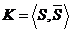– мінімальний.

⇐ Предыдущая 2 3 4 5 6 7 8910 11 Следующая ⇒