
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ДОМАШНЄ ЗАВДАННЯ. ЛІТЕРАТУРА. ПРАКТИЧНЕ ЗАНЯТТЯ №10
ДОМАШНЄ ЗАВДАННЯ
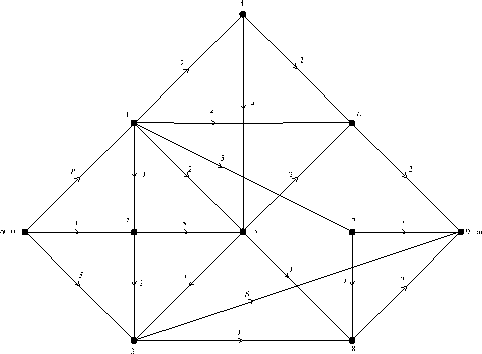
- Використовуючи алгоритм Форда і Фалкерсона, знайти максимальний потік у заданій транспортній мережі, зображеній на рисунку. На цьому рисунку поруч з кожним ребром
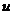 показане значення
показане значення 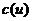 . У якості початкового потоку за алгоритмом припускаємо, що всі
. У якості початкового потоку за алгоритмом припускаємо, що всі  (позначити на рисунку самостійно).
(позначити на рисунку самостійно).
- Робота з індивідуальним завданням.
ЛІТЕРАТУРА
- Белов В. В., Воробьев Е. М., Шаталов В. Е. Теория графов. – М.: Высшая школа, 1976. – С. 114-128.
- Свами М., Тхуласираман К. Графы, сети и алгоритмы. – М.: Мир, 1984. – С. 380-418.
- Федосеева Л. И. Дискретная математика: Учеб. -практич. пособие. – Пенза: Изд-во Пенз. технол. ин-та, 1998. – С. 82-98.
ДИСКРЕТНА МАТЕМАТИКА”
ПРАКТИЧНЕ ЗАНЯТТЯ №10
Тема. “АЛГЕБРАЇЧНІ СТРУКТУРИ”.
ПЛАН
1. Поняття алгебраїчної операції.
2. Групи. Підгрупи.
3. Кільця.
4. Поля.
Завдання 1. Довести, що послідовність з чисел –1 та 1 є абелевою мультиплікативною групою.
Завдання 2. Показати на прикладі, що множення підстановок – не комутативне. Записати одиничну і обернену підстановки до підстановки А. Довести, що множина підстановок 6-го степеня є групою відносно операції множення.
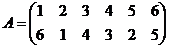 ,
, 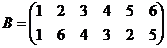 .
.
Завдання 3. Довести, що множина 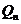 всіх скалярних матриць п-го порядку над полем дійсних чисел – комутативне кільце. (Скалярною називають матрицю
всіх скалярних матриць п-го порядку над полем дійсних чисел – комутативне кільце. (Скалярною називають матрицю 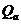 , яка має на головній діагоналі елемент a, а поза головною діагоналлю – нулі).
, яка має на головній діагоналі елемент a, а поза головною діагоналлю – нулі).
Завдання 4. Довести, що множина К всіх чисел виду 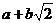 , де a і b – раціональні числа, є комутативним кільцем.
, де a і b – раціональні числа, є комутативним кільцем.
Завдання 5. Нехай С – кільце всіх комплексних чисел, а 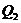 – кільце матриць 2-го порядку над полем комплексних чисел. Довести, що задане відображення є гомоморфізмом:
– кільце матриць 2-го порядку над полем комплексних чисел. Довести, що задане відображення є гомоморфізмом:
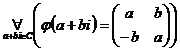 .
.
Завдання 6. Нехай 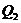 – кільце всіх матриць 2-го порядку, а
– кільце всіх матриць 2-го порядку, а 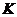 – кільце всіх чисел виду
– кільце всіх чисел виду 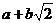 , де a і b – раціональні числа. Довести, що задане відображення є гомоморфізмом:
, де a і b – раціональні числа. Довести, що задане відображення є гомоморфізмом:
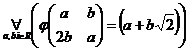 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|