ДОМАШНЄ ЗАВДАННЯ. ЛІТЕРАТУРА. ПРАКТИЧНЕ ЗАНЯТТЯ №6

ДОМАШНЄ ЗАВДАННЯ

1. Для заданих графів 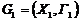і 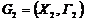побудувати матриці інциденцій, виконавши над ними відповідні операції, записати матриці інциденцій графів 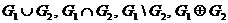. Перевірити правильність запису матриць, зобразивши ці графи геометрично.

2. 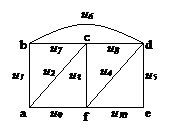Для заданого графа самостійно побудувати остов та записати матрицю незалежних циклів.

3. Робота з індивідуальним завданням.

ЛІТЕРАТУРА

1. Алферова З. В. Математическое обеспечение экономических расчетов с помощью графов. – М.: Статистика, 1994. – С. 18-23.

2. Басакер Р., Саати Т. Конечные графы и сети. – М.: Наука, 1974. – С. 30-34, 136-143.

3. Белов В. В., Воробьев Е. М., Шаталов В. Е. Теория графов. – М.: Высшая школа, 1976. – С. 43-59.

4. Свами М., Тхуласираман К. Графы, сети и алгоритмы. – М.: Мир, 1984. – С. 39-40, 105-108.

ДИСКРЕТНА МАТЕМАТИКА”

ПРАКТИЧНЕ ЗАНЯТТЯ №6

Тема. “РОЗРІЗИ ГРАФА. РОЗФАРБУВАННЯ ГРАФА”.

ПЛАН

1. Розрізи і розділяючі множини графа.

2. Матриця розрізів.

3. Розфарбування графа.

4. Хроматичне число. Хроматичний поліном.

Завдання 1. Для заданого графа 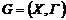побудувати розділяючу множину, всі прості розрізи і записати матрицю розрізів.

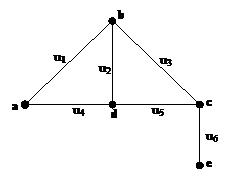Завдання 2. Якою мінімальною кількістю фарб і скількома способами можна розфарбувати дерево? Вивести формулу для знаходження 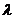і .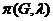

Завдання 3. Якою мінімальною кількістю фарб можна вершинно розфарбувати парний цикл? Непарний цикл? Скількома способами можна це зробити? Вивести формулу для знаходження 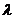і .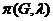

Завдання 4. Правильно вершинно розфарбувати мінімальною кількістю фарб даний граф G. Скількома способами можна це зробити?

⇐ Предыдущая 1 2 3 4 567 8 9 10 Следующая ⇒