ДОМАШНЄ ЗАВДАННЯ. ЛІТЕРАТУРА. ПРАКТИЧНЕ ЗАНЯТТЯ №8

ДОМАШНЄ ЗАВДАННЯ

1. Побудувати ейлеровий ланцюг, що складається з чотирьох ребер через задані 9 точок так, щоб цей ланцюг пройшов через всі 9 точок.

2. Робота з індивідуальним завданням.

ЛІТЕРАТУРА

1. Басакер Р., Саати Т. Конечные графы и сети. – М.: Наука, 1974. – С. 61-75.

2. Белов В. В., Воробьев Е. М., Шаталов В. Е. Теория графов. – М.: Высшая школа, 1976. – С. 168-179.

3. Свами М., Тхуласираман К. Графы, сети и алгоритмы. – М.: Мир, 1984. – С. 50-60.

4. Федосеева Л. И. Дискретная математика: Учеб. -практич. пособие. – Пенза: Изд-во Пенз. технол. ин-та, 1998. – С. 170-182.

ДИСКРЕТНА МАТЕМАТИКА”

ПРАКТИЧНЕ ЗАНЯТТЯ №8

Тема. “ПОШУК МІНІМАЛЬНИХ ШЛЯХІВ НА ГРАФАХ”.

ПЛАН

1. Пошук шляху з мінімальною кількістю дуг.

2. Пошук шляху мінімальної довжини. Алгоритм Дейкстри.

Завдання 1. Використовуючи алгоритм пошуку шляху з мінімальною кількістю дуг, знайти такий шлях з вершини А до вершини В.

Завдання 3. Використовуючи алгоритм Дейкстри, визначити найкоротші шляхи з вершини А до всіх інших вершин заданого графа.

Щоб прослідкувати дію алгоритму покроково, заповнимо такі таблиці:

§ міток LABEL (у цій таблиці відмічати вершини з незмінною міткою, обвівши мітку в квадрат. Мітки останніх вершин, помічених незмінною міткою (тобто 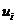) відмічати *);

§ міток PRED;

§ найкоротших шляхів

за вказаними шаблонами.

⇐ Предыдущая 2 3 4 5 6 789 10 11 Следующая ⇒