Проекция II закона Ньютонана OZ ось для m массы материала гибкого шнура ρп погонной 5 страница

Для (рис. 2. 28) второй гармоники стоячей волны, т. е. при i = 2, с λ _2ст длиной стоячей волны, равной (2. 127) λ _2ст = 2L/3, которой соответствует λ ₂ длина бегущей волны, равная λ ₂=4L/3, существуют (2. 129) два узла этой стоячей волны со следующими координатами: y_y₀ = L при m = 0; y_y₁ = L/3 при m_max = i - 1 = 1. (2. 130) Для третьей гармоники стоячей волны, т. е. i = 3, с λ _3ст длиной стоячей волной, равной (2. 127) λ _3ст = 2L/5, которой соответствует λ ₃ длина бегущей волны, равная λ ₃=4L/5, волны существует (2. 129) три узла этой стоячей волны со следующими координатами:

y_y₀ = L при m = 0; y_y₁ = 3L/5 при m = 1; y_y₂ = L/5 при m_max = i - 1 = 2. (2. 131) Общее выражение y_ym координат (рис. 2. 29) узлов закрытой с двух концов трубы, где

m = 0, 1, 2, …номер узла для первой, второй, третьей и т. д. … гармоник стоячих волн с длинами λ _1ст, λ _2ст, λ _3ст, …, cоответствующих (2. 124) длинам λ ₁, λ ₂, λ ₃, …бегущих волн, выводится приравниванием - 2Asink(L - y) амплитудной части (2. 122) уравнения нулю.

Координаты узлов y_ym определяются с учётом (2. 128) λ _i = 2L/i длины бегущей волны и (2. 70)

k_i = 2π /λ _i волнового числа из следующего выражения:

- 2Asink_i(L - y_ym ) = - 2Asin[(2π /λ _i)(L - y_ym )] = - 2Asin(2π i/2L)(L - y_ym ) = 0 ↔

↔ 2π (i/L](L - y_ym ) = mπ ↔ y_ym = L[1 - (m/i)], (2. 132)гдеm= 0, 1, 2, … номер узла для первой, второй, третьей и т. д. … гармоник, а m_max максимальное значение номера узла равно i номеру гармоники этой стоячей волны; k_i =2π /λ _i= π i/L – волновое число (2. 70), при выводе которого использовано выражение (2. 128) для λ _iдлины бегущей волны первой, второй, третьей и т. д. гармоник.

Согласно (2. 132) для (рис. 2. 29) первой гармоники стоячей волны в закрытой с двух концов трубы, т. е. i = 1, с λ _1ст длиной стоячей волны, равной L, которой соответствует λ ₁ длина бегущей волны, равная (2. 124) 2L, существует два узла этой стоячей волны с y_y₀ = L координатой (2. 132)при

m = 0 и y_y₁ = 0 координатой при m_max = i = 1.

В начальный момент t₀= 0 времени для (рис. 2. 29) первой гармоники стоячей волны результирующие (2. 122) отклонения s = s(y, t) частиц упругой среды от положения равновесия в центре трубы будут максимальны в направлении OY оси, т. е. при y = 0, будут равны (2. 122) удвоенной A амплитуде A_ст = 2A бегущей волны, т. е. в центре этой трубы будет пучность стоячей волны.

Приращение Δ p′ давления (2. 77), если L длина (рис. 2. 29) закрытой с двух концов трубы такова, что k₀L = π , в упругой среде в сечении трубы, где y = 0, т. е. у её левого конца, будет отрицательно и равно по модулю максимальному A_{Δ p}_′ отклонению давления частиц упругой среды отравновесного значения. Отрицательное приращение Δ p′ давления, т. е. растяжение, у левого конца закрытой с двух концов трубы обозначено на рис. 2. 29 бледно-голубым цветом.

В сечении трубы, где y = L, т. е. у её правого конца, приращение Δ p′ давления (2. 78) будет положительно и равно A_{Δ p}_′максимальному отклонению давления частиц упругой среды отравновесного значения. Положительное приращение Δ p′ давления, т. е. сжатие, у правого конца закрытой с двух концов трубы обозначено на рис. 2. 29 тёмно-синим цветом.

Таким образом, если L длина (рис. 2. 29) закрытой с двух концов трубы такова, что k₁L = π , то на закрытых сторонах трубы устанавливаются пучности давления стоячей плоской акустической волны, а в центре трубы устанавливается узел давления этой стоячей плоской акустической волны.

Для (рис. 2. 30) второй гармоники стоячей волны в закрытой с двух концов трубы, т. е. i = 2, с λ _2ст длиной стоячей волной, равной (2. 124) λ _2ст = L/2, которой соответствует λ ₂ длина бегущей волны, равная λ ₂= L, существует (2. 132) три узла этой стоячей волны со следующими координатами: y_y₀ = L при m = 0; y_y₁ = L/2 при m = 1; y_y₁ = 0 при m = i = 2. (2. 133)

В начальный момент t₀= 0 времени для (рис. 2. 29) первой гармоники стоячей волны результирующие (2. 122) отклонения s = s(y, t) частиц упругой среды от положения равновесия в центре закрытой с двух концов трубы будет равным нулю, т. е. в центре этой трубы будет узел стоячей волны.

Пучности результирующего (2. 123) отклонения s = s(y, t) частиц упругой среды от положения равновесия в стоячей волны, равные удвоенной A амплитуде A_ст = 2A бегущей волны, будут располагаться в y_п = L/4, y_п = 3L/4 координатах закрытой с двух концовтрубы.

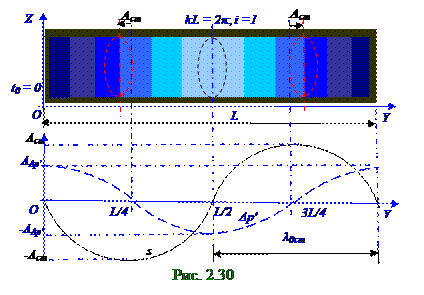
Пучности приращения Δ p′ давления стоячей плоской акустической волныв (рис. 2. 29) закрытой с двухконцов трубы для первой гармоникиэтой стоячейволны располагаются на закрытыхконцах и в центретрубы, т. е. там, где существуют узлы результирующего(2. 123) отклонения s = s(y, t) частиц упругой средыот положенияравновесия. В начальный момент t₀= 0 времени для (рис. 2. 30) второй гармоники стоячейволны на закрытых концах трубы приращение Δ p′ давления(2. 78) будет положительно и равно

A_{Δ p}_′максимальному отклонению давления частиц упругой среды отравновесного значения, т. е. упругая среда на закрытых концах трубы будет испытывать сжатие, которое обозначено на

рис. 02. 0. 30 тёмно-синим цветом.

В начальный момент t₀= 0 времени для (рис. 2. 30) второй гармоники стоячей волны в центре закрытой с двух концов трубы приращение Δ p′ давления (2. 77) будет отрицательно и равно по модулю максимальному A_{Δ p}_′ отклонению давления частиц упругой среды отравновесного значения, т. е. упругая среда в центре закрытой с двух концов трубы будет испытывать растяжение, которое обозначено на рис. 2. 30 бледно-голубым цветом.

В последующие моменты t времени стоячей волны в закрытой с двух концов трубе

y координаты узлов приращения Δ p′ давления и результирующего отклонения s = s(y, t) частиц упругой среды от положения равновесия останyтся неизменными. Координаты пучностей приращения Δ p′ давления и результирующего отклонения s = s(y, t) частиц упругой среды от положения равновесия тоже останутся неизменными, но через T_i/2 половину периодаколебаний частиц упругой среды в режиме стоячей волны i - ой гармоники знаки отклонений s = s(y, t) частиц упругой среды от положения равновесия и приращения Δ p′ давления изменятся на противоположные, т. е. положительные смещения частиц упругой среды относительно положения равновесия станут отрицательными, а положительные приращения Δ p′ давления стоячей плоской акустической волны превратятся в отрицательные.

Общее выражение координат пучностей y_п_m для (рис. 2. 27), (рис. 2. 28) закрытой с одной стороны трубы, где m= 0, 1, 2, …номер пучности для первой, второй, третьей и т. д. … гармоник стоячих волн с длинами λ _1ст, λ _2ст, λ _3ст, …, соответствующих (2. 124) длинам λ ₁, λ ₂, λ ₃, …бегущих волн, которые употребляются в уравнении стоячей волны, выводится приравниванием - 2Asink(L - y) амплитудной части (2. 122) уравнения величине 2A, т. е. максимальному отклонению s = s(y, t) частиц упругой среды от положения равновесия, вследствие чего имеет место следующее выражение: -2Asink_i(L - y_п_m ) = -2Asin{2π [(2i - 1)/4L](L - y_п_m)} = ±2A ↔

↔ 2π [(2i - 1)/4L] (L - y_пm) = (2m + 1)π /2 ↔ y_пm= L{1 - [(2m+1)/(2i-1)]}, (2. 134) гдеm = 0, 1, 2, … номер пучности для первой, второй, третьей и т. д. … гармоник стоячей волны, а

m_max максимальное значение номера пучности равно i -1 номеру гармоники этой стоячей волны;

k_i =2π /λ _i= π (2i - 1)/4L - волновое число (2. 70), при выводе которого использовано (2. 127) выражение для λ _iдлины бегущей волны первой, второй, третьей и т. д. гармоник. Для первой гармоники стоячей волны, т. е. при i = 1, с λ _1ст длиной стоячей волной, равной

λ _1ст= 2L, которой соответствует λ ₁ длина бегущей волны, равная (2. 128) λ ₁=4L, существует

(рис. 2. 27) одна пучность этой стоячей волны с (2. 134) координатой, равной y_п0 = 0 при

m_max = i - 1 = 0.

Для второй гармоники стоячей волны, т. е. при i = 2, с λ _2ст длиной стоячей волной, равной

λ _2ст = 2L/3, которой соответствует λ ₂ длина бегущей волны, равная (2. 127) λ ₂=4L/3, существуют

(рис. 2. 28) две пучности этой стоячей волны со (2. 134) следующими координатами: y_п0 = 2L/3 при m= 0; y_п1 = 0 при m_max = i - 1 = 1. (2. 135)

Общее выражение координат пучностей y_п_m для (рис. 2. 29), (рис. 2. 30) закрытой с двух концов трубы, где m = 0, 1, 2, …номер пучности для первой, второй, третьей и т. д. … гармоник стоячих волн с длинами λ _1ст, λ _2ст, λ _3ст, …, соответствующих (2. 124) длинам λ ₁, λ ₂, λ ₃, …бегущих волн, которые употребляются в уравнении стоячей волны, выводится приравниванием - 2Asink(L - y) амплитудной части (2. 122) уравнения величине 2A, т. е. максимальному отклонению s = s(y, t) частиц упругой среды от положения равновесия, вследствие чего имеет место следующее выражение:

-2Asink_i(L - y_п_m ) = -2Asin(2π i/2L)(L - y_п_m)} = ±2A ↔ (π i/L)(L - y_п_m) = (2m + 1)π /2 ↔

↔ y_пm= L[1 - (2m+1)/2i], (2. 136) гдеm = 0, 1, 2, … номер пучности для первой, второй, третьей и т. д. … гармоник стоячей волны, а

m_max максимальное значение номера пучности равно i -1 номеру гармоники этой стоячей волны;

k_i =2π /λ _i= π i/L - волновое число (2. 70), при выводе которого использовано (2. 128) выражение для

λ _iдлины бегущей волны первой, второй, третьей и т. д. гармоник. Для первой гармоники стоячей волны, т. е. при i = 1, с λ _1ст длиной стоячей волной, равной

λ _1ст= 2L, которой соответствует λ ₁ длина бегущей волны, равная (2. 128) λ ₁=2L, существует

(рис. 2. 29) одна пучность этой стоячей волны с (2. 136) координатой, равной y_п0 = L/2 при

m_max = i - 1 = 0.

Для второй гармоники стоячей волны, т. е. при i = 2, с λ _2ст длиной стоячей волной, равной

λ _2ст = L, которой соответствует λ ₂ длина бегущей волны, равная (2. 128) λ ₂=2L, существуют

(рис. 2. 30) две пучности этой стоячей волны со (2. 136) следующими координатами: y_п0 = 3L/4 при m= 0; y_п1 = L/4 при m_max = i - 1 = 1. (2. 137)

Стоячая волна в непоглощающей упругой среде: уравнения скорости смещений и относительной деформации частиц упругой среды относительно положений равновесия

Первая ∂ s/∂ t производная (2. 122) по t времени отклонения s = s(y, t) частиц упругой среды от положения равновесия в режиме стоячей волны (рис. 2. 27) в закрытой с правой стороны трубе характеризует скорость смещения этих частиц упругой среды в произвольные моменты t времени и в произвольной y координате, вследствие чего имеет место следующее выражение для этой первой

∂ s/∂ t производной по t времени: ∂ s/∂ t = - 2Aω _isink_i(L - y)cos(ω _it - k_iL), (2. 138) где ω _i = 2π v/λ _i - циклическая (2. 70) частота колебаний частиц упругой среды в режиме стоячей волны i - ой гармоники, имеющей (2. 128) λ _i длину бегущей волны.

(рис. 02. 0. 27) в закрытой с правой стороны трубе в режиме стоячей волны волнового k_i =2π /λ _i числа и λ _i=4L/(2i - 1) длины (2. 129) i - ой гармоники бегущей волны, а также координат y_ym (2. 129) узлов стоячей волны, эта sink_i(L - y) амплитудная частьвыражения (2. 136) превращается в ноль. Это соответствует свойствам стоячей волны, а именно в узлах этой стоячей волны s = s(y, t) смещения частиц упругой среды относительно положения равновесия в произвольный момент t времени отсутствуют, т. е. ∂ s/∂ t скорость смещения этих частиц упругой среды в произвольные моменты

t времени в узлах стоячей волны равны нулю.

При подстановке в sink_i(L - y) амплитуднойчасти (2. 138) выражения ∂ s/∂ t первой производной по t времени(2. 122) отклонения s = s(y, t) частиц упругой среды от положения равновесия в режиме стоячей волны волнового k_i =2π /λ _i числа и λ _i=4L/(2i - 1) длины (2. 127) i - ой гармоники бегущей волны, а также y_пm координат (2. 134) пучностей стоячей волны, эта sink_i(L - y) амплитудная частьвыражения (2. 137) превращается в единицу. Поэтому в пучностях стоячей волны ∂ s/∂ t скорость

s смещения частиц упругой среды от положения равновесия в режиме (2. 122) стоячей волны максимальны и имеют амплитуду (2. 137) этих отклонений, равную 2Aω _i.

Первая ∂ s/∂ y производная по y координате(2. 122) отклонения s = s(y, t) частиц упругой среды от положения равновесия в режиме стоячей волны (рис. 2. 27) в закрытой с правой стороны трубе характеризует (2. 91) ε = ∂ s/∂ y относительную деформацию этой упругой среды, которая численно равна значению длины, на которую расширился или сжался рассматриваемый объем упругой средыпри распространении в нём продольной волны, отнесённый к длины этого объема упругой среды, вследствие чего имеет место следующее выражение для этой первой ∂ s/∂ y производной по y координате: ∂ s/∂ y = - 2k_iAcosk_i(L - y) sin(ω _it - k_iL ), (2. 139) где ω _i = 2π v/λ _i - циклическая (2. 70) частота колебаний частиц упругой среды в режиме стоячей волны i - ой гармоники, имеющей (2. 128) λ _i длину бегущей волны.

k_i =2π /λ _i числа и λ _i=4L/(2i - 1) длины (2. 127) i - ой гармоники бегущей волны, а также координат y_ym (2. 129) узлов стоячей волны, эта cosk_i(L - y) амплитудная частьвыражения (2. 139) превращается в единицу. Поэтому в узлах стоячей волны (2. 90) ε = ∂ s/∂ y относительная деформация упругой среды максимальна и имеет амплитуду, равную (2. 139) 2Ak_i.

При подстановке в cosk_i(L - y) амплитуднойчасти (2. 139) выражения ∂ s/∂ y первой производной по y координате(2. 122) отклонения s = s(y, t) частиц упругой среды от положения равновесия в режиме стоячей волны волнового k_i =2π /λ _i числа и λ _i=4L/(2i - 1) длины (2. 127) i - ой гармоники бегущей волны, а также координат y_п_m (2. 134) пучностей стоячей волны, эта cosk_i(L - y) амплитудная частьвыражения (2. 139) превращается в нулю. Поэтому в пучностях стоячей волны (2. 90) ε = ∂ s/∂ y относительная деформация упругой среды отсутствует.

⇐ Предыдущая 1 2 3 4 5 67