
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Проекция II закона Ньютонана OZ ось для m массы материала гибкого шнура ρп погонной 2 страница
Приближённые " ≈ " равенства в (2. 82) выражении введены вследствие малости относительного отклонения, т. е. деформации (∂ s/∂ y) < < 1 при s отклонениях частиц от положения равновесия в произвольный момент t времени. В (2. 82) сначала было использовано разложение выражения
[1 + (∂ s/∂ y)]γ в ряд по степеням (∂ s/∂ y) с пренебрежением членами высших порядков малости, а потом использовано приближенное равенство: 1/[1 + γ (∂ s/∂ y)] ≈ [1 - γ (∂ s/∂ y)], которое справедливо при γ (∂ s/∂ x) < < 1.
Первая производная от выражения(2. 82) по y имеет следующий вид:
∂ P ′ /∂ y = -γ P(∂ 2s/∂ y2). (2. 83) Подставляем (2. 80) в (2. 82) и получаем следующее одномерное волновое уравнение распространения акустических волн в линейной однородной изотропной непоглощающей упругой среде: ∂ 2s/∂ y2 = ρ (∂ 2s/∂ t2)/γ p ↔ ∂ 2s/∂ y2 = (1/v2)(∂ 2s/∂ t2), (2. 84) где (γ P/ρ )1/2 = v - фазовая (рис. 2. 18), (рис. 2. 19) скорость распространения звуковой волны в направлении k волнового вектора, перпендикулярного плоской волновой поверхности S площадью поперечного сечения области газа.
Из уравнения Менделеева - Клапейрона (4. 13) из раздела 4. 1 " Физическая термодинамика" для идеального газа при постоянном pдавлении имеет место следующее выражение: P/ρ =RT/μ ↔ ρ = Pμ /RT, (2. 85) где R - универсальная газовая постоянная; T - термодинамическая температура; μ - масса одного моля газа; ρ - плотность этогогаза.
Подставляем (2. 85) ρ плотности в выражение (2. 84), после чего фазовая v скорость распространения звуковой волны в газе в принимает следующий вид: v = (γ RT/μ )1/2. (2. 86)
Средняя < v> скорость теплового движения молекул газа(4. 268) из раздела 4. 2 " Физическая термодинамика" имеет следующий вид: < v> = (8RT/π μ )1/2. (2. 87) Сравнивая (2. 86) и (2. 87) получаем следующее соотношение фазовой v скорости распространения звуковой волны в газе со средней < v> скоростью теплового движения молекул газа: v = < v> (γ π /8)1/2 ≈ (3/4)< v> . (2. 88) Согласно (2. 88) фазовая v скорость распространения звуковой волны в газе одного порядка со средней < v> скоростью теплового движения молекул газа.
По аналогии с одномерным (2. 85) волновым уравнением распространение акустических волн в линейной однородной изотропной непоглощающей упругой среде с учетомs отклонения от положения равновесия частиц этой среды в произвольный момент t времени в произвольной точке трехмерного пространства с декартовыми x, y и z координатами описывается следующим трёхмерным волновым уравнением: (∂ 2s/∂ x2) + (∂ 2s/∂ y2) + (∂ 2s/∂ z2) = (1/v2)(∂ 2s/∂ t2), (2. 89) гдеv фазовая скорость распространения звуковой волны в любом направлении трёхмерного пространства вследствие свойства изотропности этого пространства и любой точке с
x, y и z координатамивследствие однородности трёхмерного пространства.
Волновое уравнение, фазовая скорость распространения продольных упругих волн в стержнях
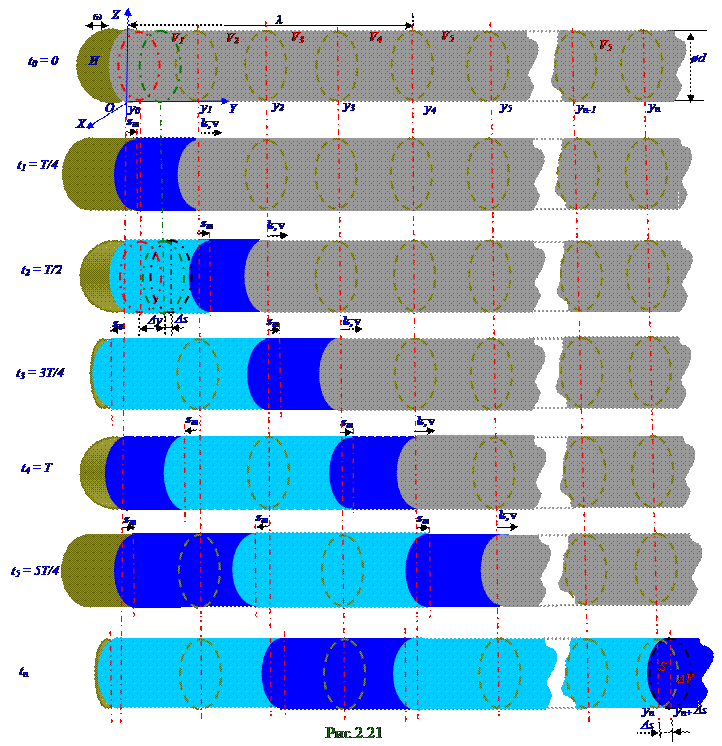
Фазовая v скорость распространения продольной упругой волны в тонком стержне определяется из волнового уравнение распространения этих упругих продольных волн в тонких стержнях, когда ø d диаметр (рис. 2. 21) стержня много меньше λ длины упругой волны, т. е. когда ø d< < λ . Упругая продольная волна в тонком стержне по аналогии (рис. 2. 18) с звуковой волной в газе представляет собой (рис. 2. 21) последовательность чередующихся областей (синий цвет) сжатия и (голубой цвет) расширения, распространяющихся в направлении k волнового вектора, т. е. вдоль оси этого тонкого стержня в положительную сторону OY оси. Вследствие колебаний c (2. 3)
T = 2π /ω периодом гармонических колебаний (рис. 2. 21) внешнего И источника звука, например, пьезоэлектрического вибратора, V1 объем тонкого стержня, находящегося между сечениями газа с y0, y1 координатами, в интервал (рис. 2. 21) времени от 0 до T/4 испытывает (синий цвет) сжатие.
В интервал (рис. 2. 21) времени от T/4 до T/2 объем V1 тонкого стержня испытывает
(голубой цвет) расширение, вследствие чего малый объем тонкого стержня Δ y длиной, находящийся в начальный момент t0 = 0 времени в (серый цвет) недеформированном состоянии, расширяется на малую Δ s длину. Поэтому этот малый объем тонкого стержня Δ y длиной к моменту T/2 времени имеет
∂ s/∂ y относительную деформацию, которая определяется следующим предельным переходом от малой
Δ y длины тонкого стержня, который получил малую Δ s деформацию: ε = limΔ s / Δ y = ∂ s/∂ y, (2. 90) Δ y→ 0
где ε = ∂ s/∂ y - относительная деформация численно равна значению длины, на которую расширился или сжался рассматриваемый объем тонкого стержня при распространении в нём упругих продольных волн, отнесённой к длине этого тонкого стержня. При расширении объема тонкого стержня ε = ∂ s/∂ y относительная деформация больше нуля, т. к. (2. 90) при расширении Δ s > 0. При сжатии объема тонкого стержня ε = ∂ s/∂ y относительная деформация меньше нуля, т. к. (2. 90) при сжатии Δ s < 0.
При малых продольных деформациях рассматриваемый объем тонкого стержня характеризуетсяσ напряжением, котороесогласнозакону Гука имеет следующее выражение:
σ = Eε , (2. 91)
где E, Н/м2 - модуль Юнга, характеризующий прочностные свойства тонкого стержня, а именно, равный силе, которую надо приложить к тонкому стержню с единичным поперечным сечением, чтобы ε относительная деформация в нём равнялась единице, т. е. когда (2. 90) малая Δ y длина недеформированного стержня под воздействием приложенной силы увеличилась на величину малой
Δ s = Δ y деформации; σ , Н/м2 - напряжение в площади поперечного сечения тонкого стержня, расположенной в y координате; напряжение σ , Н/м2 численно равно результирующей силе,
приложенной в данной y координате к единичной площади поперечного сечения тонкого стержня с
вектором этой результирующей силы, направленным перпендикулярно поперечному сечению тонкого стержня; напряжение σ , Н/м2 в площади поперечного сечения тонкого стержня, расположенным в
y координате тонкого стержня, имеет знак ε относительной деформации в этой площади поперечного сечения тонкого стержня: при расширении объема в данной площади поперечного сечения тонкого стержня ε = ∂ s/∂ y относительная деформация (2. 90) больше нуля, поэтому напряжение σ , Н/м2 в этой площади тоже больше нуля; при сжатии объема в данной площади поперечного сечения тонкого стержня ε = ∂ s/∂ y относительная деформация (2. 90) меньше нуля, поэтому напряжение σ , Н/м2 в этой площади тоже меньше нуля.
На рис. 2. 22 по аналогии с рис. 2. 20, где изображено приращение Δ V объёма газа при распространении в нём звуковой волны, представлен отдельно от всего (рис. 2. 21) тонкого стержня малый Δ V объем этого тонкого стержня Δ s длиной и S площадью поперечного сечения, испытывающий в момент tn времени расширение.
При расширении малого Δ V объема тонкого стержня к правой чёрной стенке приложен вектор F yn+ Δ s силы упругой деформации в положительном направлении OY оси, вследствие чего эта правая чёрная стенка удалилась от левой зелёной стенки малого Δ V объема тонкого стержня на малую
Δ s длину и заняла положение с yn+ Δ s координатой. К левой зелёной стенке малого Δ V объема тонкого стержня, имеющей в недеформированном состоянии yn координату, приложенвектор F yn силы упругой деформации, который противодействует вектору F yn+ Δ s силы упругой деформации в приложенной в данной y координате к единичной площади поперечного сечения тонкого стержня с
вектором этой результирующей силы, направленным перпендикулярно поперечному сечению тонкого стержня; напряжение σ , Н/м2 в площади поперечного сечения тонкого стержня, расположенным в
y координате тонкого стержня, имеет знак ε относительной деформации в этой площади поперечного сечения тонкого стержня: при расширении объема в данной площади поперечного сечения тонкого стержня ε = ∂ s/∂ y относительная деформация (2. 90) больше нуля, поэтому напряжение σ , Н/м2 в этой площади тоже больше нуля; при сжатии объема в данной площади поперечного сечения тонкого стержня ε = ∂ s/∂ y относительная деформация (2. 90) меньше нуля, поэтому напряжение σ , Н/м2 в этой площади тоже меньше нуля.
На рис. 2. 22 по аналогии с рис. 2. 20, где изображено приращение Δ V объёма газа при распространении в нём звуковой волны, представлен отдельно от всего (рис. 2. 21) тонкого стержня малый Δ V объем этого тонкого стержня Δ s длиной и S площадью поперечного сечения, испытывающий в момент tn времени расширение.
При расширении малого Δ V объема тонкого стержня к правой чёрной стенке приложен вектор F yn+ Δ s силы упругой деформации в положительном направлении OY оси, вследствие чего эта правая чёрная стенка удалилась от левой зелёной стенки малого Δ V объема тонкого стержня на малую
Δ s длину и заняла положение с yn+ Δ s координатой. К левой зелёной стенке малого Δ V объема тонкого стержня, имеющей в недеформированном состоянии yn координату, приложенвектор F yn силы упругой деформации, который противодействует вектору F yn+ Δ s силы упругой деформации в правой чёрной стенки с yn+ Δ s координатой. Когда под воздействием вектора F yn+ Δ s силы упругой деформации у правой чёрной стенки с yn+ Δ s координатой образовался малый Δ V объем расширения тонкого стержня Δ s длиной и S площадью поперечного сечения, у левой зелёной стенки малого Δ V объема возникает вектор F yn силы упругой деформации, противодействующий этому расширению. Направлен этот вектор F yn силы упругой деформации в отрицательном направлении OY оси, т. е. противоположно вектору F yn+ Δ s силы упругой
При расширении малого Δ V объема тонкого стержня к правой чёрной стенке приложен вектор F yn+ Δ s силы упругой деформации в положительном направлении OY оси, вследствие чего эта правая чёрная стенка удалилась от левой зелёной стенки малого Δ V объема тонкого стержня на малую
Δ s длину и заняла положение с yn+ Δ s координатой. К левой зелёной стенке малого Δ V объема тонкого стержня, имеющей в недеформированном состоянии yn координату, приложенвектор F yn силы упругой деформации, который противодействует вектору F yn+ Δ s силы упругой деформации в правой чёрной стенки с yn+ Δ s координатой. Когда под воздействием вектора F yn+ Δ s силы упругой деформации у правой чёрной стенки с yn+ Δ s координатой образовался малый Δ V объем расширения тонкого стержня Δ s длиной и S площадью поперечного сечения, у левой зелёной стенки малого Δ V объема возникает вектор F yn силы упругой деформации, противодействующий этому расширению.
Направлен этот вектор F yn силы упругой деформации в отрицательном направлении OY оси, т. е. противоположно вектору F yn+ Δ s силы упругой деформации в правой чёрной стенки с yn+ Δ s координатой, а F yn модуль вектора F yn силы упругой деформации у левой зелёной стенки малого Δ V объема меньше Fyn+ Δ s модуля вектору F yn+ Δ s силы упругой деформации в правой чёрной стенки с yn+ Δ s координатой, потому что в противном случае не происходило бы расширения малого Δ V объема на Δ s длину в положительном направлении OY оси.
|
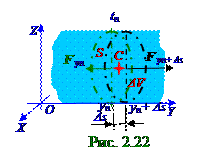
где ∂ 2s/∂ t2 - проекция вектора ∂ 2 s /∂ t2 ускорения на OY ось (рис. 2. 22) центра C масс малого Δ V объема тонкого стержня при его расширении на Δ s длину в положительном направлении OY оси;
(Fyn+ Δ s)y = Fyn+ Δ s - проекция на OY ось вектора F yn+ Δ s силы упругой деформации, который направлен в положительную сторону OY оси; (Fyn)y = - | F yn | - проекция на OY ось вектора F yn силы упругой деформации, который направлен в отрицательную сторону OY оси, что в (2. 93) учтено знаком " -" минус перед | F yn | модулем этого вектора F yn силы упругой деформации.
Модули Fyn+ Δ s, | F yn | векторов соответственно F yn+ Δ s силы упругой деформации в правой чёрной стенки с yn+ Δ s координатой и F y силы упругой деформации у левой зелёной стенки с yn координатой, имеют с учётом (2. 91) следующие значения: Fyn+ Δ s = Sσ yn+ Δ s; | F yn | = Sσ yn, (2. 93) где σ yn+ Δ s, σ yn- напряжения (2. 91), (2. 93) в площадях поперечного сечения тонкого стержня, расположенных соответственно yn+ Δ s и yn координатах, которые имеют положительные значения, поскольку малый Δ V объем тонкого стержня Δ s длиной (рис. 02. 0. 22) во всех своих площадях поперечного сечения расширяется.
Подставляем (2. 93) в (2. 92) и получаем следующее выражение проекции II закона Ньютонана OY осьдля m массы материала тонкого стержня ρ плотностью, заключённой в (рис. 2. 22) малом объеме Δ V = SΔ s:
OY: ρ SΔ s(∂ 2s/∂ t2) = Fyn+ Δ s - | F yn | ↔ ρ SΔ s(∂ 2s/∂ t2) = S(σ yn+ Δ s - σ yn) ↔ ρ Δ s(∂ 2s/∂ t2) = σ yn+ Δ s - σ yn. (2. 94)
На малом промежутке от yn до yn+ Δ s координат тонкого стержня σ (y)функция, которая представляет собой σ , Н/м2 напряжение в S площади, расположенной в yn ≤ y ≤ yn+ Δ s координате этоготонкого стержня, и σ '(y) производная от σ , Н/м2 напряжения непрерывны, поэтому согласно теореме Лагранжа для разности σ yn+ Δ s - σ yn напряжений, имеет место следующее выражение:
σ yn+ Δ s - σ yn = (∂ σ /∂ у)[( yn+ Δ s) - yn] ↔ σ yn+ Δ s - σ yn = (∂ σ /∂ у)Δ s. (2. 95)
Подставляем (2. 90) в (2. 95) и получаем следующее выражение для разности
σ yn+ Δ s - σ yn напряжений в площадях поперечного сечения тонкого стержня, расположенных соответственно yn+ Δ s и yn координатах, т. е. (рис. 2. 22) в левой зелёной и правой чёрной стенках малого Δ V объема тонкого стержня Δ s длиной, испытывающего в момент tn времени расширение: σ yn+ Δ s - σ yn = (∂ σ /∂ у)Δ s ↔ σ yn+ Δ s - σ yn = E[∂ (∂ s/∂ y)/∂ y]Δ s ↔ σ yn+ Δ s - σ yn = E(∂ 2s/∂ y2)Δ s. (2. 96)
Подставляем (2. 96) в (2. 94) и получаем по аналогии с (2. 84) акустической волной следующее одномерное волновое уравнение распространения продольных волн в линейной однородной изотропной непоглощающей упругой среде:
E(∂ 2s/∂ y2)Δ s = ρ Δ s(∂ 2s/∂ t2) ↔ ∂ 2s/∂ y2 = (ρ /E)(∂ 2s/∂ t2) ↔ ∂ 2s/∂ y2 = (1/v2)(∂ 2s/∂ t2), (2. 97) где (E/ρ )1/2 = v - фазовая (рис. 2. 21) скорость распространения продольной волны в линейной однородной изотропной непоглощающей упругой среде в направлении k волнового вектора, перпендикулярного плоской поверхности S площадью поперечного сечения тонкого стержня.
Волновое уравнение, фазовая скорость распространения поперечных волн в гибком шнуре
Фазовая v скорость распространения поперечных волн в
(рис. 2. 23) натянутом с F силой гибком шнуреопределяется из волнового уравнение, когда имеют место малые s отклонения площади поперечного сечения гибкого шнура относительно положения равновесия в направлении, перпендикулярном длине этого гибкого шнура.
|





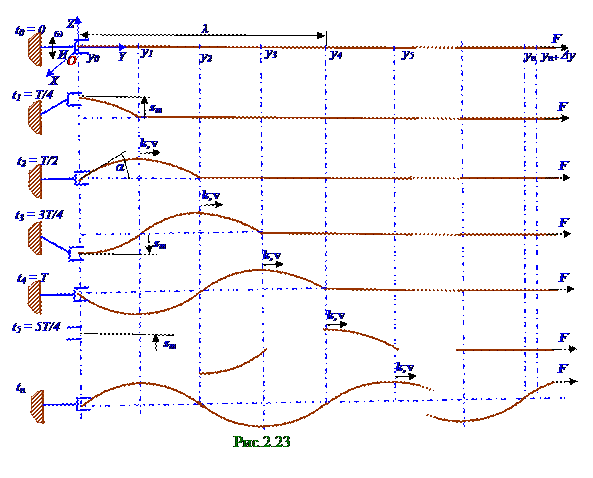
отклоняется вверх, т. е. в положительную сторону OZ оси. Участок гибкого шнура с y0 координатой в момент t1 = T/4 времени отклоняется (рис. 2. 23) по OZ оси относительно положения равновесия на sm максимальное или амплитудное значение.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|