Вращающийся Aвектор, равный сумме векторов A1 иA2 , изображающих соответственногармонические колебания 1 - го грузикаотносительно 2- го грузикаи гармонические колебания

Система, совершающая колебания, называется колебательной системой. Свободными колебаниями, т. е. собственными колебаниями называются колебания, которые происходят в отсутствие внешних воздействий на колебательную систему и возникают вследствие какого-либо начального отклонения этой системы от состояния её устойчивого равновесия. Колебания называются периодическими, если значения всех физических величин, характеризующих колебательную систему и изменяющихся при её колебаниях, повторяются черезравные промежутки времени. Наименьший промежутокTвремени, удовлетворяющий этому условию, называется Tпериодом колебаний. За Tпериод колебаний система совершает одно полное колебание. Частотойν периодических колебанийназывается величина ν = 1/T, равная числу полных колебаний, совершающихся за единицу времени. Циклической или круговой(2. 2) частотой периодических колебаний, называется величина ω = 2π ν = 2π /T, равная числу полных колебаний, умноженное на 2π радиан. При периодических колебаниях s отклонения физической величины от положения равновесия в зависимости от t времени удовлетворяет следующему условию: s(t) = s(t + T). Периодические s = s(t) колебания физической величины называются гармоническими, если s отклонения физической величины от положения равновесия в зависимости от t времени соответствуют следующим уравнениям: s =A cos(ω t+ φ 0) или s = A sin(ω t+ φ 1), (2. 8) где ω = 2π ν = 2π /T = const - циклическаяили круговая частота гармонических колебаний; A = sмакс = const > 0 - максимальное отклонение колеблющейсяфизической sвеличиныот состояния её устойчивого равновесия, называемое амплитудойколебаний; φ 0 и φ 1 = φ 0 + π /2 - начальные фазы колеблющейсяфизической sвеличины. Значение физическойsвеличины впроизвольный моментtвремениопределяется значением (2. 28) фазы колебаний Ф = ω t+ φ 0 или Ф = ω t+ φ 1. Величины φ 0 и φ 1 представляют собой начальные фазыколебаний, т. е. значение Ф0 колебания физическойвеличины в момент t0 = 0 времени. Перваяv = v(t) = ds/dt и вторая

a = a(t) = d²s/dt² производные по времени от гармонически колеблющейся s(t) =A cos(ω t+ φ ₀) физической величины также совершают гармонические колебания с той же циклической ω частотой в соответствии со следующими уравнениями: v = ds/dt = - Aω sin(ω t+ φ ₀) = Aω cos(ω t+ φ ₀+π /2); (2. 9) a = d²s/dt² = - Aω ²cos(ω t+ φ ₀) = Aω ²cos(ω t+ φ ₀+π ), (2. 10) где v = v(t) и a = a(t) модули векторов v = v (t), a = a (t) соответственно скорости и ускорения колеблющейся физической s = s(t) величины; Aω и Aω ² - амплитуды соответственно модулей v(t) скорости и a(t) ускоренияколеблющейся физической величины. Из сравнения (2. 8) и (2. 9) начальная фаза модуля v(t) = ds/dt скорости колеблющейся физической s(t) величины опережает начальную фазу этой самой физической s(t) величины на π /2 угол. Из сравнения (2. 8) и (2. 10) начальная фаза модуля a(t) = d²s/dt² ускорения колеблющейся физической s(t) величины опережает начальную фазу этой самой физическойs(t) величины наπ угол.

На рис. 2. 2 построены графики физической s(t) величины - сплошной линией, ds/dt скорости - штриховой линией и d²s/dt² ускорения - штрих - пунктирнойлинией колебаний относительно

устойчивого равновесия этой физической s(t)величиныдля случая равенства начальнойφ ₀ или φ ₁ = φ ₀ + π /2 фазыколебаний нулю, т. е. когда в (2. 8) φ ₀ = 0 или φ ₁ = φ ₀ + π /2 = 0.

Представление гармонических колебаний на векторной диаграмме

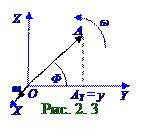
Гармоническиеколебания представляют (рис. 2. 3) с помощью векторной диаграммы. Для этого из начала Oкоординат проводят A вектор, модуль которого равен Aамплитуде рассматриваемых колебаний и составляет с OY осью угол Φ = ω t + φ ₀, равный фазе колебаний в данный момент t времени. С течениемвремени Φ уголувеличивается так, что A вектор равномерно вращается вокруг начала Oкоординат c модулем ω (1. 19) из раздела 1. 0 " Физические основы механики" вектора ω угловой скорости вращения.

Проекция A_Y вектора A на горизонтальную OY ось совершает гармонические колебания по (2. 7) закону, имеющая следующее выражение: A_Y = y = Acos(ω t+ φ ₀), (2. 11)

где (рис. 2. 3) проекция A_Y вектора A на горизонтальную OY ось численно равна в данный момент

t времени y координате конца этого A вектора.

Графическое изображение гармонических колебаний посредством вращающегося вектора называется методом векторной диаграммы.

Согласно формуле Эйлера e^iφ = cosφ + isinφ для комплексных чисел, где i - мнимая единица, гармонические колебания (2. 7), записанные в экспоненциальной форме, имеют следующий вид: ỹ = Aexpi(ω t+ φ ₀)= Ã expiω t, (2. 12) где Ã = Aexpiφ ₀ - комплексная амплитуда. Действительная часть комплексной ỹ функции, обозначаемая Re ỹ , соответствует (2. 7) уравнению гармонических колебаний и имеет следующее выражение: Reỹ = y = Acos(ω t+ φ ₀), (2. 13) где в отличие от (рис. 2. 1) гармонические колебания происходят не по OZ, а по OY оси координат.

Сложение гармонических колебаний одного направления равных и близких частот

Под сложением колебаний понимают нахождение уравнения, согласно которому в произвольный момент t времени определяют результирующее отклонение колеблющейся системы от положения равновесия, когда эта система одновременно участвует в нескольких колебательных процессах.

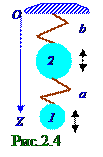
Грузик 1 - ый (рис. 2. 4) колеблется на a пружине относительно 2- го грузика по следующему уравнению: z₁ = A₁cos(ω ₁t+ φ ₁), (2. 14) где z₁ - координата 1 - го грузика, т. е. отклонение от положения равновесия 1 - го грузика в зависимости от t времени в системе координат, связанной со 2 - ым грузиком; A₁и ω ₁ - соответственно (2. 2) амплитуда и циклическая частота гармонических колебаний 1 - го грузика на а пружине относительно 2- го грузика; φ ₁, рад - начальная фаза приколебаниях 1 - го грузика на

a пружине относительно 2- го грузика, определяющее z₁₀координату 1 - го грузика в системе координат, связанной со 2 - ым грузиком, в начальный момент t₀ времени, т. е. когда t = t₀= 0.

Грузик 1 - ый (рис. 2. 4) колеблется на b пружине вместе со 2 - ым грузиком по следующему уравнению: z₂ = A₂cos(ω ₂t+ φ ₂ ), (2. 15) где z₂- координата 1 - го грузика, т. е. отклонение от положения равновесия 1 - го грузика в зависимости от t времени, когда он колеблется как единое целое со 2 - ым грузиком на b пружине относительно O начала координат; A₂и ω ₂ - соответственно амплитуда и циклическая (2. 2) частота гармонических колебаний 1 - го и 2- го грузиков на b пружине относительно O начала координат; φ ₂, рад - начальная фаза приколебаниях 1 - го грузика на b пружине как единое целое со 2 - ым грузиком относительно O начала координат, определяющее z₁₀координату 1 - го грузика

относительно O начала координат, в начальный момент t₀ времени, т. е. когда t = t₀= 0. Результирующее колебание 1 - го грузика относительно O начала координат определится из сложениядвух одинаково направленныхгармонических колебаний, которое производится (рис. 2. 3) методом векторной диаграммы. На рис. 2. 5 изображены A₁ иA₂векторы, которые вращаются (рис. 2. 3) с модулями циклическихω ₁и ω ₂частот вращениясоответственно против часовой стрелки и представляют гармонические колебания1 - го (2. 14) и2- го (2. 15) грузиков

в данный момент t времени.

Вращающийся Aвектор, равный сумме векторов A1 иA2, изображающих соответственногармонические колебания 1 - го грузикаотносительно 2- го грузикаи гармонические колебания

2 грузика вместе с 1 грузиком относительно O начала координат в произвольный момент

t времени, т. е. A = A ₁ + A₂, изображает результирующее колебание 1 грузика относительно O начала координат.

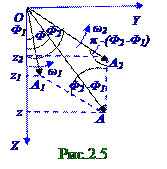
Фазы колебаний 1 - го (2. 14) и2- го (2. 15) грузиков на рис. 2. 5 в данный момент t времени обозначены соответственно Ф₁ и Ф₂, а фаза Ф результирующего колебания 1 - го грузика относительно O начала координат обозначена Ф. В произвольный момент времени Ф₁ и Ф₂ фазы колебаний 1 - го (2. 14) и2- го (2. 15) грузиков имеют следующий вид:

Ф₁ = ω ₁ t+ φ ₁; Ф₂ = ω ₂ t+ φ ₂. (2. 16)

Результирующее z поOZоси колебание 1 - го грузика относительно O начала координат определится следующим сложением двух одинаково направленных гармонических колебаний z₁1 - го (2. 14) грузика относительно 2- го грузика (рис. 02. 0. 4) и z₂2- го (2. 15) грузика относительно O начала координат:

z = z₁ + z₂ = A₁cos(ω ₁t+ φ ₁) + A₂cos(ω ₂t+ φ ₂ ) = AcosФ, (2. 17) где A и Ф - соответственно амплитуда и фаза результирующих гармонических колебаний 1 - го грузика относительноO начала координат; z - результирующая координата 1 - го грузика, т. е. отклонение от положения равновесия 1 - го грузика в зависимости от t времени, когда учитываются его (2. 11) z₁ колебания на а пружине в системе координат, связанной со 2 - ым грузиком, а также учитываются его (2. 12) z₂колебанияна b пружине как единое целое со 2 - ым грузиком относительно O начала координат.

Амплитуда(2. 17) Aрезультирующих гармонических колебаний1 - го грузика относительно O начала координат равна A модулю результирующеговектора A (рис. 2. 5)навекторной диаграмме. По теореме косинусов A модуль результирующеговектора A (рис. 2. 5)навекторной диаграмме имеет следующий вид: A = {A₁² + A₂² - 2A₁A₂ cos [π -(Ф₂-Ф₁)]}^1/2== [A₁² + A₂² + 2A₁A₂cos (Ф₂-Ф₁)]^1/2. (2. 18) В выражении (2. 18) Ф₂ - Ф₁ является разностью Ф₂ фазыгармонических

колебаний 2- го грузика вместе с 1 - ым грузиком относительно O начала координат в произвольный момент t времени и Ф₁ фазы гармонических колебаний 1 - го грузика относительно 2- го грузика.

Фаза Ф результирующего вектора A (рис. 2. 5)на векторной диаграмме результирующего поOZ оси колебания 1 - го грузика относительно O начала координат в (2. 14) выраженииимеет следующий вид: tgФ = (A₁sinФ₁+ A₂sinФ₂)/(A₁cosФ₁+ A₂cosФ₂) ↔ ↔ Ф = arctg[(A₁sinФ₁+ A₂sinФ₂)/(A₁cosФ₁+ A₂cosФ₂)]. (2. 19) Два z₁ и z₂ гармонических колебания называются когерентными, если Ф₂ - Ф₁ разностьих фаз не зависит от t времени и имеет следующий вид: Ф₂ - Ф₁ = (ω ₂ - ω ₁)t + (φ ₂ - φ ₁) = const (2. 20) Выполнение условия (2. 20) возможно, если ω ₂ = ω ₁ = ω . Тогда Ф₂ - Ф₁ разностьфаз когерентных колебаний равна следующей φ ₂ - φ ₁разности их начальных фаз: Ф₂ - Ф₁ = φ ₂ - φ ₁= φ ₀. (2. 21) При выполнении (2. 21) условия результирующее (2. 17)z колебание двух складываемых

z₁ и z₂ гармонических колебаний одного направления является тоже гармоническим с той же циклической ω частотой, что и эти складываемые колебания, вследствие чего z результирующееколебание двух складываемых z₁ и z₂ гармонических колебаний имеет следующий вид: z = z₁ + z₂ = Acos(ω t + φ ₀). (2. 22) Выражение для A амплитуды результирующего колебания как суммы двух когерентных колебаний получается подстановкой (2. 21) Ф₂ - Ф₁ = φ ₂ - φ ₁ разностифаз когерентных колебаний в (2. 18), вследствие чего получается следующее выражение: A = [A ₁ ² + A ₂ ² + 2A ₁ A ₂ cos(φ ₂ - φ ₁)]^1/2, (2. 23)

Выражение(2. 19) начальной Ф₀ фазы результирующего колебания как суммы двух когерентных колебаний получается подстановкой в (2. 13) начального t₀ времени, равного нулю, т. е. t₀= 0, вследствие чего получается следующее выражение для начальной Ф₀ фазы результирующего колебания: Ф₁₀ = φ ₁; Ф₂₀ = φ ₂↔ tgФ₀ = (A₁sinφ ₁+ A₂sin φ ₂)/(A₁cos φ ₁+ A₂cos φ ₂) ↔ ↔ Ф₀ = arctg[(A₁sinφ ₁+ A₂sinφ ₂)/(A₁cosφ ₁+ A₂cosφ ₂)], (2. 24)где (2. 14) A₁, φ ₁, рад - соответственно амплитуда и начальная фаза приколебаниях 1 - го грузика на a пружине относительно 2- го грузика; (2. 15) A₂, φ ₂, рад - соответственно амплитуда и начальная фаза приколебаниях 1 - го грузика на b пружине как единое целое со 2 - ым грузиком относительно O начала координат.

В зависимости от значения φ ₂ - φ _{1 =}φ ₀ разности начальных фаз складываемых колебаний

A амплитуда результирующего колебания согласно выражению (2. 23) изменяется в следующих пределах: от A = | A ₁ - A ₂ | при φ ₂ - φ ₁= ±(2m + 1)π (2. 25) до A = A ₁ + A ₂ при φ ₂ - φ ₁ = ±2mπ , (2. 26) где m = 0, 1, 2, … - любое целое неотрицательное число.

Если (2. 26) φ ₂ - φ ₁= φ ₀= ±2mπ , т. е. разность начальных фаз складываемых когерентных колебаний кратна 2π , то говорят, что складываемые колебания физической величины синфазны. В случае сложения синфазных механических, электромагнитных или электромеханических колебаний A амплитуда результирующего колебания складываемых физических величин максимальна.

Если (2. 25) φ ₂ - φ ₁= φ ₀= ±(2m + 1)π , т. е. разность начальных фаз складываемых когерентных колебаний кратна нечётному числу π , то говорят, что складываемые колебания физической величины противофазны. В случае сложения противофазных механических, электромагнитных или электромеханических колебаний A амплитуда результирующего колебания складываемых физических величин минимальна.

Результирующие колебания двух складываемых (2. 17) гармонических колебаний одного направления, циклические (2. 2) частоты ω ₁и ω ₂ колебаний которых различны, т. е. ω ₂ ≠ ω ₁, являются некогерентными колебаниями, т. к. разность их фаз Ф = Ф₂ - Ф₁ = (ω ₂ - ω ₁)t + (φ ₂ - φ ₁) непрерывно изменяется с течением t времени. При сложении таких колебаний получаются негармонические результирующие колебания. Негармонические колебания, получающиеся в результате сложения двух одинаково направленных гармонических колебаний с близкими ω ₁, ω ₂ (2. 14), (2. 15) циклическими частотами, т. е. | ω ₂ - ω ₁| < < ω ₁, называются биениями.

Сложение взаимно перпендикулярных гармонических колебаний равных и кратных частот.

Пусть материальная M точка одновременно колеблется вдоль OY и OZ осей координат в соответствии со следующими уравнениями: x = A₁cos(ω t + φ ₁) ; y = A₂cos(ω t + φ ₂ ), (2. 27) где x, y - координата материальной M точки в зависимости от t времени при колебаниях соответственновдоль OX и OY осей координат; ω - циклическая частота(2. 2) гармонических колебаний материальной M точки, одинаковая по OX и OY осям координат; A₁, φ ₁, рад - соответственно амплитуда и начальная фаза приколебаниях материальной M точки по OY оси;

A₂, φ ₂, рад - соответственно амплитуда и начальная фаза приколебаниях материальной M точки по OZ оси.

УравнениеТ траектории (рис. 2. 6) результирующего движения материальной M точки в

OYZ плоскости можно найти, выразив из (2. 24) уравнения y = A₂cos(ω t+ φ ₂ ) колебания материальной M точки по OY оси параметр ω t =[arcos(y/A₂)]- φ ₂, подставив этот параметр ω t в уравнение

x = A₁cos(ω t+ φ ₁) колебания материальной M точки по OY оси. Исключив таким образом из уравнений (2. 27) t времени, получаем следующее уравнениеТ траектории результирующего движения материальной M точки в OXY плоскости:

(x²/A₁²) + (y²/A₂²) - (2xy/A₁A₂)cos(φ ₂- φ ₁) = sin²(φ ₂- φ ₁). (2. 28)

На OXY плоскости (2. 28) уравнение Т траектории результирующего движения материальной M точки представляет собой эллипс с A₁ и A₂полуосями, равными (2. 27) A₁ и A₂амплитудам складываемых взаимно перпендикулярных гармонических колебаний этой материальной M точки.

Ориентация в OYZ плоскости осей эллипса, а также его размеры зависят от A₁ и A₂амплитудскладываемых(2. 24)взаимно перпендикулярных гармоническихколебанийматериальнойM точкии φ ₂- φ ₁разности начальных фазэтихскладываемыхколебаний. Если в (2. 28) φ ₂- φ ₁ = ±(2m + 1)π /2, где m = 0, 1, 2, …, n, то оси эллипса,

являющегося Т траекторией (рис. 2. 6) результирующего движения материальной M точки в

OXY плоскости, совпадают с OX и OY осями координат, а размеры полуосей этого эллипса равны

A₁ и A₂амплитудам складываемых (2. 24) взаимно перпендикулярных гармонических колебаний материальной M точки.

Уравнение Т траектории результирующего движения материальной M точки (2. 28) в этом случае примет следующий вид: (x²/A₁²) + (y²/A₂²) = 1. (2. 29) Материальная M точка, колеблющаяся вдоль взаимно перпендикулярных направлений с одинаковой циклической (2. 2)ω частотой, совершает один полный оборот по Т траектории, представляющий собой(рис. 02. 0. 6) эллипс, за время, равное T = 2π /ω периоду складываемых колебаний.

Если A₁ и A₂амплитуды складываемых (2. 27) взаимно перпендикулярных гармонических колебаний материальной M точки равны друг другу, т. е. A₁ = A₂, то Т траектория (2. 29) результирующего движения материальной M точки представляет собой окружность.

В тех случаях, когда φ ₂- φ ₁разность начальных фаз складываемых колебаний кратна π , т. е. φ ₂- φ ₁= ±mπ , где m = 0, 1, 2, …, n, то Т траектория (2. 28) результирующего движения материальной M точкииз эллипса вырождается в отрезок прямой, вследствие чего уравнение Т траектории этого результирующего движения материальной M точки примет следующий вид: y = ± ( A₁/ A₂)x. (2. 30) Знак " +" в выражении (2. 30) соответствует сложению взаимно перпендикулярных гармонических колебаний, когда эти колебания синфазны, а знак " -" соответствует сложению противофазных колебаний.

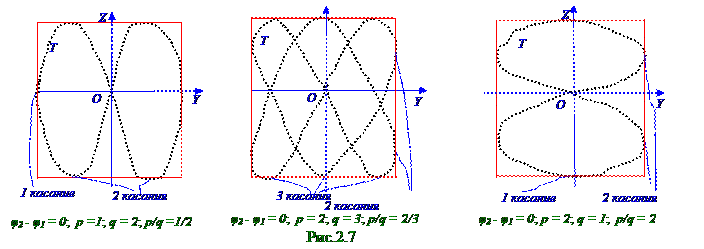
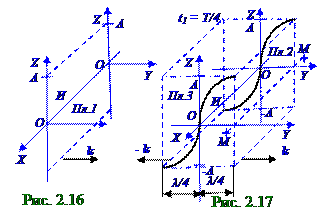
Сложение взаимно перпендикулярных гармонических колебаний с циклическими частотами pω и qω , где p и q - целые числа: y= A₁cos(pω t+ φ ₁); z = A₂cos(qω t+ φ ₂), где p и q - целые числа, приводит к движению материальной M точкипо траектории, названной фигурой Лиссажу. На рис. 2. 7 приведены различные случаи Т траекторий движения материальной M точки, колеблющейся во взаимно перпендикулярных направлениях с указанными соотношениями циклических pω и qω частот.

Отношение частот pω и qω складываемых колебаний равно отношению числа касаний соответствующей им фигуры Лиссажу со стороной прямоугольника, параллельной OZ оси, и со стороной, параллельной OY оси.

Динамика гармонических колебаний. Кинетическая и потенциальная энергия гармонического осциллятора и импульс гармонического осциллятора

У некоторых механических систем потенциальная W_p энергия является функцией одной переменной. Если у такой механической системы существует устойчивое положение равновесия, в котором потенциальная W_p энергия этой механической системы имеет минимум, а полная

W_Σ энергия, т. е. сумма кинетической W_k и потенциальной W_p энергии, величина постоянная, т. е. не зависят от t времени, то такую механическую систему называют гармоническим осциллятором.

В гармоническим осцилляторе материальная точка m массой совершает свободные незатухающие колебания под действием упругой или квазиупругой силы.

Гармоническим осцилляторомявляется пружинный маятник(рис. 2. 8), у которого материальная точкаm массой совершает незатухающие свободные, вследствие отсутствия сил сопротивления, прямолинейные гармоническиеколебания с циклическойω ₀ (2. 2) частотой относительно O началакоординат, которое находится в точке устойчивогоравновесия этого пружинного маятника. Второй законНьютонав проекции на OY ось с учётом направлениявектора Δ y смещения (рис. 2. 8) пружинного маятника относительно устойчивогоположения равновесияпо правилу определения проекций (2. 1) и по аналогии с (2. 2) имеет следующий вид: OY: m(d²y/dt²) = F_упр_y; F_упр_y = - mω ₀²y ↔ m(d²y/dt²) = - mω ₀²y, (2. 31) где ω ₀² = χ /m - квадрат циклической частоты гармонических колебаний пружинного маятника; Δ y - проекция на OY ось вектора Δ y смещения

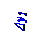
пружинного маятника заменена аналогично (2. 2) равной этой Δ y проекции величиной y координаты, отсчитанной от O начала координат, которое находится в точке устойчивого равновесия пружинного маятника.

В (2. 31) применено равенство m(d²y/dt²) = F_упр_y потому, что по OY оси на материальную точку m массой действует единственная сила, которой является (рис. 2. 8) сила упругости пружины, вектор F_упр (1. 106)из раздела 1. 0 " Физические основы механики " которой является равнодействующим

вектором силы, приложенным к материальной точке. Приложенные по OZ оси к материальной точке m массой вектора m g силы тяжести и N силы реакции опоры уравновешивают друг друга.                     Если пружинный (рис. 2. 8) маятник растянут, т. е. y₁координата материальной точки m массой больше нуля, то векторы a₁ ускорения и F _{1 упр}силы упругости коллинеарны j единичному вектору (1. 1) из раздела 1. 0 " Физические основы механики " и направлены противоположно этому

j единичному вектору.

       Если пружинный (рис. 2. 8) маятник сжат, т. е. y₂ координата материальной точки m массой меньше нуля, то векторы a₂ ускорения и F _{2 упр}силы упругости коллинеарны j единичному вектору (1. 1) из раздела 1. 0 " Физические основы механики " и направлены в одну сторону с этим

j единичным вектором.

       По аналогии с (1. 99) – (1. 109) из раздела 1. 0 " Физические основы механики " и с

учётом (2. 31) определяем W_p потенциальную энергию материальной точки m массой при её отклонении (2. 28) на величину y = s(t) = A cos(ω t+ φ ₀) относительно равновесия под воздействием упругой силы F_упр_y в заданный момент t времени из следующего выражения:

                                                                        W_py

       dW_p = - F_упр_ydy ↔ dW_p = mω ₀²ydy ↔ W_p = ∫ dW_p = ∫ mω ₀ ²ydy = (mω ₀ ²y²)/2 =                                                                                                 0     0

                                 = (mω ₀²A²/2)cos²(ω ₀t+ φ ₀) = (mω ₀²A²/4)[1+ cos(2ω ₀t+2φ ₀)].            (2. 32)        Согласно (2. 32) W_p потенциальная энергия, графическая зависимость которой на рис. 02. 0. 9 от величины отклонения Δ y пружинного маятника относительно положения равновесия изображена короткими пунктирными линиями оранжевого цвета, минимальна в точке устойчивого равновесия

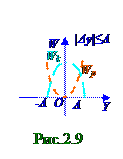
этого пружинного маятника, совпадающей сOначаломкоординат. При максимальном отклонениипружинного маятникаотположенияравновесия, когда модуль |Δ y| вектора Δ y смещения равенамплитуде колебанийэтого пружинного маятника, т. е. |Δ y| = y = A, потенциальнаяW_pэнергиясогласно (2. 33) становится равной (mω ₀ ²A²)/2. Согласно (2. 33) W_pпотенциальная энергия, графическая зависимость которой на рис. 02. 0. 9 от величины отклонения Δ y пружинного маятникаотносительно положения равновесия изображена короткимипунктирными линиями оранжевого цвета, минимальна в точке устойчивогоравновесия этого







пружинного маятника, совпадающей сO началом координат.

       При максимальном отклонении пружинного маятникаотположения равновесия, когда модуль |Δ y| вектора Δ y смещения равен амплитуде колебаний этого пружинного маятника, т. е.          |Δ y| = y = A, потенциальная W_p энергия согласно (2. 33) становится равной (mω ₀ ²A²)/2.                        Потенциальная W_p энергия (2. 32) пружинного маятника изменяется с циклической 2ω ₀ (2. 2) частотой в 2 раза превышающей ω ₀ циклическую частоту прямолинейных гармонических колебаний (рис. 2. 8) материальной точки m массой.

       Кинетическая W_k энергия (1. 88) из раздела 1. 0 " Физические основы механики " материальной точки m массой, совершающей прямолинейные гармонические колебания по OY оси с учетом (2. 9) ds/dt = dx/dt = v = - Aω sin(ω t+ φ ₀) скорости смещения этойматериальной точки m массой в произвольный момент t времени имеет следующий вид:      W_k = mv²/2 =                                                                                      = (mω ₀²A²/2) sin²(ω ₀t+ φ ₀) = (mω ₀²A²/4)[1 - cos(2ω ₀ t+2φ ₀)] =                                                                  = (mω ₀²A²/2)[1 - cos²(ω ₀t + φ ₀)] = (mω ₀²/2)(A²- y²).             (2. 33)     Согласно (2. 33)W_k кинетическая энергия, графическая зависимость которой на рис. 2. 9 от величины отклонения Δ y пружинного маятника относительно положения равновесия изображена длинными пунктирными линиями бирюзового цвета, максимальна в точке устойчивого равновесия этого пружинного маятника, совпадающей с O началом координат. При максимальном отклонении пружинного маятникаотположения равновесия, когда модуль |Δ y| вектора Δ y смещения равен амплитуде колебаний этого пружинного маятника, т. е. |Δ y| = y = A, кинетическая W_k энергия согласно (2. 33) становитсяравной нулю.

Полная механическая энергия и импульс гармонического осциллятора

       Сумма (2. 32) и (2. 33) - это полная W_Σ механическая энергия материальной точки m массой(рис. 2. 8), сместившейся под воздействием F_x_упр упругой силы в момент t времени в y координату, отсчитанной от O начала координат, которое находится в точке устойчивого равновесия материальной точки m массой, вследствие чего эта полная W_Σ механическая энергия колеблющейся материальной точки m массой имеет следующий вид:                                              W_Σ = W_k + W_p =                                  = (mω ₀²A²/4)[1 - cos(2ω ₀t+2φ ₀)] + (mω ₀²A²/4)[1+ cos(2ω ₀t+2φ ₀)] = (mω ₀²A²/2) = const.     (2. 34)       Таким образом, пружинный маятник (рис. 2. 8), совершающий прямолинейные гармонические колебания обладает всеми следующими 3-мя признаками гармонического осциллятора:

- его W_p потенциальная энергия (2. 32)являетсяфункцией одной переменной;

- у него существует положение устойчивого равновесия (рис. 2. 8), вкоторомW_p потенциальная энергияравна нулю;

- его W_Σ полная (2. 34) механическая энергия в произвольный момент t времени постоянна.             Модуль pвектора p импульса гармонического осциллятора (1. 41) из раздела 1. 0 " Физические основы механики " с учетом (2. 29) ds/dt = dy/dt = v = Aω cos(ω t+ φ ₀+π /2) скорости смещения материальной точки m массой в произвольный момент t времени относительно положения равновесияимеет следующий вид:                            p = mv = mAω cos(ω ₀t+ φ ₀+π /2).            (2. 35)



                                 Фазовая траектория колебательной системы

    Фазовой траекторией колебательной системы называется представление на OYZ плоскости (рис. 2. 11) зависимости момента импульса или импульса этой колебательной системы от соответственно угла отклонения при угловых колебаниях или смещения при прямолинейных колебаниях от положения устойчивого равновесия.

dα /dt

Математический маятник(рис. 2. 10), представляющий собой подвешенную на невесомой нити l длиной материальнуюточку m массой, имеет α уголотклонения от OZ оси, изменяющийсяво времени по следующему кинематическому уравнению:                                                                                        α = α ₀cosω ₀t,       (2. 36) где α ₀ и ω ₀ - соответственно амплитуда угла отклонения математического маятника относительно OZ оси и циклическая частотаегосвободных незатухающих гармонических колебаний.



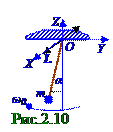
       Проекция dα /dt на OX ось вращения вектора d α /dt угловой скорости, который (рис. 2. 10) направлен противоположно OX оси, т. к. математический маятник в данный момент t времени вращается вокруг OX оси по часовой стрелке, согласно (1. 18) из раздела 1. 0 " Физические основы механики " имеет следующий вид:                   dα /dt = - α ₀ω ₀sinω t = α ₀ω ₀cos(ω ₀t + π /2),       (2. 37) где α ₀ω ₀ - амплитуда проекции dα /dt на OX ось вектора d α /dt угловой скорости этого математического маятника. Умножаем (2. 37) на момент J_OX инерции (1. 63) из раздела 1. 0 " Физические основы механики " математического маятника относительно OX оси вращенияи получаем L_OXпроекцию на эту OX ось вращения (1. 74) из раздела 1. 0 " Физические основы механики " вектора L момента импульса математического маятника в произвольный момент t времени.

       Проекция L_OXна OX ось вращения вектора L момента импульса математического маятника в данный момент t времени положительна, т. к. этот вектор (рис. 2. 10) L момента импульса коллинеарен вектору d α /dt угловой скорости и направлен с ним в противоположную сторону, и имеет следующий вид:                                                                        L_OX= J_OXα ₀ω ₀cos(ω ₀t + π /2),    (2. 38)

где J_O_Xα ₀ω ₀ - амплитуда проекции L_OX на OX ось вращения вектора L момента импульса математического маятника.

    Исключениемв (2. 36) и (2. 38) t времени получается выражение проекции L_OXна OX ось вращения вектора L момента импульса математического маятника в зависимости отα угла (рис. 2. 10) отклонения этого математического маятника относительно OX оси в данный момент

t времени, которое имеет следующий вид:                         [L_OX²/J_OX²α ₀²ω ₀ ²)] + α ²/α ₀² = 1.     (2. 39)

α ; Y Y

На OXY плоскости (рис. 2. 11), где по OY оси наносится величина α угла отклонения математического маятника, а по OX оси наносится величина проекции L_OXна   OX ось вращения (рис. 2. 10) вектора L момента импульса математического маятника, уравнение (2. 39) представляет эллипс. Этот (рис. 2. 11) эллипс представляет собой фазовую траекториюколебаний



математического маятника. Величина полуоси (рис. 2. 11) эллипса по OY оси равна (рис. 2. 10)

амплитуде α ₀ угла отклонения математического маятника, а величина полуоси (рис. 2. 11) этого эллипса по OX оси равна (рис. 2. 10) амплитуде J_OXα ₀ω ₀ проекции L_OX на OX ось вращениявектора L момента импульса математического маятника.

       Согласно рис. 2. 11при максимальном α ₀ угловом отклонении математического маятника от положения равновесия момент импульса этого математического маятника равен нулю иравна (1. 94) из раздела 1. 0 " Физические основы механики " нулю кинетическая W_kэнергия математического маятника. При прохождении математическим маятником (рис. 2. 10) положения равновесия, т. е. при

α угловом отклонении, равным нулю, потенциальная W_p энергия в OXY системе координат

(рис. 2. 10) равна нулю, а кинетическая W_kэнергия этого математического маятника, вследствие максимального значения (2. 36) dα /dt модуля вектора d α /dt угловой скорости будет максимальна и согласно (1. 112) из раздела 1. 0 " Физические основы механики " будет равна полной

W механической энергии этого математического маятника, имеющей следующий вид:                                                                                                                                                            W = J_OX²α ₀²ω ₀ ²/2.   (2. 40)       Таким образом, анализ фазовой траектории колебательной системыдаёт возможность изучать характер движения и энергетические характеристики этойколебательной системы.

Дифференциальное уравнение гармонических колебаний физического маятника и его решение



       Физический маятник (ФМ)- это любое тело, имеющее возможность совершать колебательные движения относительно положения равновесия под действием вектора m g силы тяжести (рис. 2. 12) вокруг неподвижной горизонтальной OX оси, не проходящей через C центр массы тела и называемой осью качания маятника.

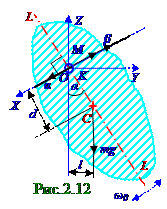
Точка K пересечения OX осикачанияФМ и LLперпендикуляромкней, называется точкой подвеса этого ФМ. В отсутствие сил тренияв подвесе уравнение движения ФМ, колеблющегося вокруг OX оси с учетом уравнения изменения момента импульса механической системы (1. 76) из раздела 1. 0 " Физические основы механики", имеет следующий вид:                             OX: J_OX(d²α /dt²) = - mgdsinα , (2. 41)      где J_OX -момент инерции маятникаотносительно OX оси, α - угол поворота относительно положения равновесия маятника, d²α /dt² = β - проекция на OX ось вектора β углового ускоренияФМ, который m - масса маятника; " - mgdsinα " - проекция М_X на OX ось качания маятника вектора М (рис. 2. 12) момента от вектора mg силы тяжести

относительно (1. 62) из раздела 1. 0 " Физические основы механики " O полюса, которым (рис. 2. 12) является начало O координат; dsinα = l -плечо вектора m g силы тяжести относительно этого

O полюса. Вектор М момента вектора m g силы тяжести направлен противоположно OX оси и поэтому имеет отрицательную проекцию М _X на OX ось. При малых α углах колебания маятника sinα ≈ α и уравнение (2. 41) принимает следующий вид:                                   d²α /dt² + (mgd/J_OX)α = 0,     (2. 42)

       Выражение (2. 43) – это дифференциальное (2. 2) уравнение гармонических колебаний, решение которого имеет следующий вид:                                              α = α ₀cos(ω ₀t + φ ₀),       (2. 43) где α ₀ и φ ₀ - соответственно амплитуда и начальная фаза колебаний, которые определяют аналогично(2. 5) выражению.

       В (2. 43) присутствуют следующие выражения: ω ₀ = ( mgd)/J_OX)^1/2 и T₀ = 2π [J_OX/( mgd)]^1/2. (2. 44) соответственно ω ₀ циклическая частота и T₀ период гармонических малых колебаний физического маятника.

Квазиупругая сила колебательной системы

Согласно выражению (2. 32) вектор F равнодействующей приложенных сил, приводящий к гармоническим колебаниям по OY оси, имеет следующий вид: F = - mω ₀ ²Δ y.                     (2. 45)       В гармоническим осцилляторе, которым, в частности, является (рис. 2. 8) пружинный маятник, эта сила имеет упругий характер. Вектор F_упр упругой силы направлен в противоположную сторону вектору Δ y смещения пружинного маятника, направленного (рис. 2. 8) от      O начала координат, относительно которого происходит колебание этого пружинного маятника. Силы иной физической природы, но обладающие свойством иметь направление, противоположное вектору смещения, называются квазиупругими силами. Такие силы тоже вызывают в системе гармонические колебания. При колебаниях (рис. 2. 12) физического маятника по (2. 40) уравнению роль квазиупругой силы выполняет вектор М момента вектора m g силы тяжести. Вектор М моментанаправлен противоположно вектору α угла отклонения.

    Дифференциальное уравнение свободных затухающих колебаний и его решение



       В отличие от пружинного маятника на рис. 2. 1 на маятник (рис. 2. 13) при возвратно - поступательном движении с вектором v скорости относительно Н направляющих кромевектора      F_упр силы упругости пружины и вектора m g силы тяжести тела m массой действует также вектор    F_c силы сопротивления, например, возникающий вследствие трения тела m массой о                          Н направляющие. Вектор F_c силы сопротивления направлен противоположно вектору

v =(dz/dt) k скорости движения тела m массой и имеет следующий вид: F_c = - r(dz/dt) k= -r v,     (2. 46) где r = const > 0 - коэффициент сопротивления.

            Вектор v скоростидвижения тела m массой в данный момент t времени принят на рис. 2. 13 направленным в сторону, противоположную k единичному вектору.

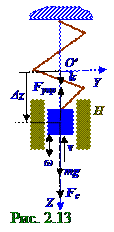
Второй закон Ньютонав проекции на OZ ось для тела m массой с учетом (2. 2) и вектора F_c силы сопротивления, который направлен в сторону OZ оси, т. е. коллинеарен k единичному векторуи направлен с ним в одну и ту же сторону, вследствие чего имеет место следующее выражение:                                         OZ: m(d²z/dt²) = mg - F_Z_{уп р}+ F_Zc ↔ m(d²z/dt²) = - kΔ z+ r(dz/dt)cos(v, ^k) ↔ ↔ m(d²z/dt²) + r(dz/dt) + kΔ z = 0 ↔ (d²z/dt²) + 2β (dz/dt) + zω ₀ ² = 0,      (2. 47) где cos(v, ^k) = - 1, т. к. вектор vскорости движения тела m массойв данный момент времениколлинеарен k единичному векторуи направлен в противоположнуюсторону этому k единичному вектору; β = r/2m > 0 - коэффициент затухания; ω ₀ = (k/m)^1/2 - циклическая частота гармоническихколебаний пружинного маятника, т. е. в отсутствие потерь энергии, когда β коэффициент затухания равен нулю, т. е. β = 0.



       В выражении (2. 47) проекция Δ z на OZ осьвектора Δ z смещения пружинного маятника заменена равной этой проекции Δ z величиной z координаты, отсчитанной от O' начала координат в состоянии статического удлинения пружины, относительно которого происходит колебание пружинного маятника

       Если затухание не слишком велико, что выполняется при β < ω ₀, то зависимость z(t) смещения (рис. 2. 13) тела m массой, совершающего на пружине свободные затухающие колебания относительно статического удлинения пружинного маятника, т. е. относительно O' начала координат, в зависимости от t времени, имеет следующий вид:                           z = A₀e^-β^tcos(ω t + φ ₀),      (2. 48) где ω = (ω ₀²- β ²)^1/2- циклическая частота свободных затухающих колебаний пружинного маятника.

       Постоянные величины A₀ и φ ₀ в (2. 49) соответственно начальная амплитуда и начальная фаза колебаний определяются из начальных условий, в которых находится пружинный маятник в момент начала t₀ времени, т. е. t₀ = 0, свободных затухающих колебаний этого пружинного маятника по следующим выражениям:                    z₀ = A₀cosφ ₀ и v₀_Z = (dz/dt)_t0=0 = - A₀(β cos φ ₀ + ω sinφ ₀),    (2. 49) где z₀ иv₀_Z - соответственно начальное отклонение, отсчитанной от O' начала координат в состоянии (рис. 2. 1) статического удлинения пружины, и проекция на OZ ось вектора v₀начальной скорости тела m массой. Величины z₀ иv₀_Z задаются в условии задач. Неизвестные величины

A₀ и φ ₀ определяются из решения системы (2. 49) двух уравнений с двумя неизвестными.                                 Период T и циклическая ω частота свободных затухающих колебаний согласно (2. 3) связаны следующим соотношением:                                                   T = 2π /ω =2π /(ω ₀ ²- β ²)^1/2 (2. 50) При увеличении β коэффициента затухания T период свободных затухающих колебаний возрастает и обращается согласно (2. 50) в бесконечность при равенстве (2. 47) β коэффициента затухания ω ₀ циклической (2. 2)частоте гармонических колебаний. Таким образом, при β = ω ₀, колебания в механической системе отсутствуют.

       Если β > ω ₀, то зависимость z(t) смещения (рис. 2. 13) тела m массой относительно O' начала координат в зависимости от t времени, что является решением дифференциального (2. 49) уравнения, имеет следующий вид:                                   z = C₁exp-α ₁ t + C₂ exp-α ₂ t,                             (2. 51)

где α ₁ = β + (β ² - ω ₀²)^1/2 и α ₂ = β - (β ² - ω ₀²)^1/2, а C₁ и C₂ - постоянные коэффициенты, которые определяются аналогично (2. 49) из задания z₀ иv₀_Z - соответственно начального отклонение, отсчитанной от O' начала координат в состоянии (рис. 2. 1) статического удлинения пружины, и проекции на OZ ось вектора v₀начальной скорости тела.

       Согласно решению (2. 51) дифференциального (2. 47) уравнения при превышении                          β коэффициента затухания ω ₀ циклической частоты смещение Δ z = z (рис. 2. 13) тела   m массой относительно положения равновесия носит апериодический характер и с учётом (2. 51) α ₁> α ₂ в установившемся состоянии, т. е. при t → ∞ , смещение Δ z = z тела m массой относительно положения равновесия стремится к нулю.

       Таким образом, в установившемся состоянии при апериодическом (2. 51) характере движения тело стремится к своему положению равновесия.



       Логарифмический декремент затухающих колебаний. Добротность колебательной                                                        системы



       Логарифмическим δ декрементом затухания называется безразмерная величина, равная натуральному логарифму отношения амплитуд затухающих колебаний в моменты t и (t + T) времении имеющая следующий вид:                                           δ = ln(A₀e^-β^t/A₀e^{-β (}^t+^T)) = β T.         (2. 52)      Число N колебаний, по происшествию которых A₀e^-β^t амплитуда свободных затухающих колебаний уменьшается в e раз, связано с выражением (2. 52) логарифмического δ декремента затухания следующим соотношением:                    (A₀e^-β^t)/( A₀e^{-β (}^t+^NT)) = e ↔ β NT = 1 ↔ N = 1/δ .     (2. 53)      Время τ релаксации, по истечению которого A₀e^-β^t амплитуда свободных затухающих колебаний уменьшается в e разсвязано с учётом(2. 52), (2. 53)с β коэффициентом затухания следующим выражением:                                                                           τ = NT ↔ τ = 1/β .      (2. 54)     Связь между ω циклической частотой свободных затухающих колебаний, ω ₀ циклической частотой гармонических колебаний и δ логарифмическим декрементом затухания устанавливается следующим выражением:                                                     ω = ω ₀[1 - (ω /ω ₀)²(δ /2π )²]^1/2.       (2. 55)     Добротностью Q колебательной системы называется безразмерная физическая величина, равная произведению 2π на отношение W(t) энергии колебаний системы в произвольный момент

t временик убыли этой энергии за промежуток времени от t до (t + T), т. е. за один период свободных затухающих колебаний, вследствие чего выражение для Q добротности колебательной системы имеет следующий вид:                                                      Q = 2π W(t)/[(W(t) - W(t + T))]. (2. 56)       Квадрат амплитуды свободных затухающих колебаний в произвольный момент

t времени согласно (2. 48)равен A₀²e^-2β^t, а (2. 34) полная W_Σ механическая энергия колеблющейся материальной точки m массой пропорциональна квадрату амплитуды колебаний, поэтому с учетом этого выражение (2. 56) принимает следующий вид:                                                                                                                     Q =2π (A₀²e^{-2 β}^t)/( A₀²e ^{-2 β}^t- A₀²e ^{-2 β (}^t+^T)) = 2π /(1 - e^-2β^T) = 2π /(1- e^-2δ).        (2. 57) где δ (2. 52) - логарифмический декремент затухания.



        Дифференциальное уравнение вынужденных колебаний и его решение

       При приложении к пружинному маятнику помимо (рис. 2. 13) вектора F_c силы сопротивления вектора F_в = F₀ cosΩ t внешней периодической силы (рис. 02. 0. 14)дифференциальное (2. 48) уравнение в проекции на OZ осьпринимает следующий вид:

       OZ: m(d²z/dt²) = mg - F_Z_{уп р} - F_Zc + F_Z_в↔ m(d²z/dt²) = - kΔ z - r(dz/dt) cos( v, ^k ) + F₀ cosΩ t ↔

            ↔ md²z/dt²= - kΔ z - r(dz/dt) + F₀ cosΩ t ↔   d²z/dt²+ 2β (dz/dt )+ ω ₀²z =( F₀/m) cosΩ t.    (2. 58)          Зависимость z(t) смещения (рис. 2. 14) тела m массой, совершающего на пружине вынужденные гармонические колебания относительно статического удлинения пружинного маятника, т. е. относительно O' начала координат, в зависимости от t времени, что является решением дифференциального (2. 58) уравнения, содержит два слагаемых и имеет следующий вид:                                                                                                                   z = z₁(t) + z₂(t).                        (2. 59)

       Первое z₁(t) слагаемое в (2. 59) соответствует (2. 48) свободным затухающим колебаниям пружинного маятника. Второе z₂(t) слагаемое в (2. 59) соответствует гармоническим колебаниям пружинного маятника с Ω циклической частотой, равной Ω циклической частоте вектора

F_в = k F₀ cosΩ t внешней периодической силы, где F₀ - амплитуда модуля F_в вектора F_в внешней периодической силы.

       Амплитудное значение z₁(t) свободных затухающих колебаний, равное (2. 48) A₀e^-β^t, уменьшается соответственно значению (2. 48)β коэффициента затухания. Через 5τ промежуток времени, где (2. 54) τ - время релаксации, амплитуда A_5τ свободных затухающих колебанийстановится равной следующему значению:                              A_5τ = A₀exp - β (t₀+ 5τ ) = A₀/e⁵≈ A/166, (2. 60)

где t₀ = 0 и A₀ – соответственномомент времени начала колебанийи начальная амплитуда колебаний в этот начальный момент t₀времени.

       Следовательно, через некоторое время после начала колебаний свободные z₁(t) колебания пружинного маятника практически прекращаются. Пружинный маятник переходит в состояние установившихся вынужденных гармонических колебаний в зависимости от t времени, что является следующим решением дифференциального (2. 58) уравнения:                   z =A_в cos(Ω t - φ ₀). (2. 61)

АмплитудаA_вустановившихся вынужденных гармонических колебаний и отставание φ ₀фазы гармонических колебаний z смещения пружинного маятника относительно положения равновесия от фазы гармонических колебаний вектора F_в=kF₀ cosΩ tвнешней периодической силы(рис. 2. 14)зависят от соотношения между Ω циклическими частотами вынужденных гармонических колебанийи ω ₀ (2. 2) гармонических колебаний, а также зависят от β коэффициента(2. 48) затухания этого пружинного маятника в соответствии со следующими выражениями:                                     A_в= F₀/m[(ω ₀² - Ω ²)² + 4β ²Ω ²]^1/2 и tgφ ₀ = 2β Ω /(ω ₀² - Ω ²)         (2. 62) При Ω = 0 получим в установившемся состоянии из (2. 61) φ ₀ = 0 и A_в = F₀/mω ₀² = F₀/χ , где χ -коэффициент(2. 1) жесткости пружины, т. е. маятник колебаться не будет, а будет иметь статическое смещение из положения равновесияпод действием вектора F_в= kF₀ постояннойсилы. F_в= kF₀ постояннойсилы.



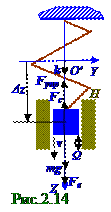
       При Ω → ∞ получим в установившемся состоянии из (2. 62) амплитуду A_в→ 0 и

tgφ ₀→ 0, а φ ₀→ π .



                                                         Механический резонанс колебательных процессов

       Амплитуда (2. 62) A_в смещения z(t) (рис. 2. 14) тела m массой, совершающего на пружине вынужденные гармонические колебания относительно статического удлинения пружинного маятника, т. е. относительно O' начала координат, в зависимости от t времени, достигает максимума при Ω _р циклической резонансной частоте гармонических колебаний вектора F_в = k F₀ cosΩ _рt внешней периодической силы. Эта Ω _р циклическая резонансная частота гармонических колебаний связана с ω ₀ циклической (2. 2 ) частотой гармонических колебаний пружинного маятника и его (2. 47)

β коэффициентом затухания следующим выражением:       Ω _р = (ω ₀ ²- 2β ²)^1/2 = (ω ²- β ²)^1/2, (2. 63) где ω - циклическая частота свободных затухающих колебаний маятника.

       На амплитудной характеристике (рис. 2. 15а) вынужденных гармонических колебаний с увеличением β коэффициента, т. е. β ₃ > β ₂ > β ₁, циклическая Ω _р резонансная частота уменьшается, т. е. Ω _р3 < Ω _р2< Ω _р1, c одновременным уменьшением A_в резонансной амплитуды колебаний, т. е.

A_в3 < A_в2< A_в1. Если Ω циклическая частота гармонических колебаний вектора F_в = k F₀ cosΩ _рt внешней периодической силы равна нулю, т. е. Ω = 0, то амплитуда A_в смещения z(t) (рис. 2. 14) тела

m массойравна F₀/mω ₀², т. е. маятник не колеблется, а имеет статическое смешение из положения равновесия под действием вектора F_в = k F₀ постоянной во t времени силы.

       При (рис. 2. 15а) равенстве β ₁ коэффициента затухания нулю, т. е. при β ₁= 0, и равенстве

Ω _р циклической частотыгармонических колебаний вектора F_в = i F₀ cosΩ _рt внешней периодической силы циклической ω ₀ (2. 2) частоте гармонических колебаний у пружинного маятника наступает резонанс, при котором (2. 62) A_в амплитуда установившихся вынужденных колебаний (рис. 2. 15а) стремится к бесконечности, т. е. A_в→ ∞ .

       При конечном значении β коэффициента затухания резонансная A_вр амплитуда колебаний или максимальная амплитуда, которая получается при подстановке (2. 63) Ω _р циклической резонансной частоты гармонических колебаний вектора F_в = k F₀ cosΩ _рt внешней периодической силы в (2. 62) выражение, имеет следующий вид:                                 A_вр = F₀/2mβ ω = π F₀/mδ ω ²,             (2. 64)

где использованы выражения (2. 54) δ = β T - логарифмического декремента затухания и(2. 50)

T = 2π /ω - периода T свободных затухающих колебаний.

На рис. 2. 15б изображена фазо - частотная характеристика установившихся вынужденных гармонических колебаний маятника.

       При равенстве Ω циклической частоты гармонических колебаний вектора внешней периодической силы F_в = k F₀cosΩ t циклической ω ₀ частоте гармонических колебаний отставание

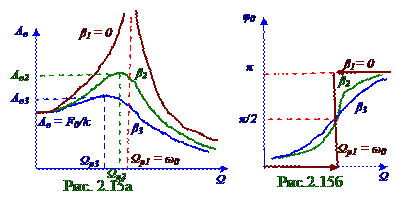
φ ₀фазы гармонических колебаний z смещения пружинного маятника относительно положения равновесия от фазы гармонических колебаний этого вектора F_в=kF₀cosΩ tвнешней периодической силыравен π /2. Это значит, что при значении F_в модуля вектора F_в=kF₀cosΩ t внешней периодической силы, равному своему максимальному значению, т. е. F_в = F₀, смещение колеблющейся системы относительно





положения равновесия равно нулю.

       При Ω < ω ₀смещение и периодическая сила находятся в фазе, т. е. направления вектора силы и вектора смещения колеблющейся системы совпадают. При Ω > ω ₀ смещение и периодическая сила находятся в противофазе, т. е. направления вектора силы и вектора смещения колеблющейся системынаправленыв противоположные стороны.

    Виды механических волн. Основы акустики. Элементы физиологической акустики.

       Упругой волной называют процесс распространения возмущения в упругой среде. При этом происходит распространение именно возмущения частиц среды, но сами частицы испытывают движение около своих положений равновесия. Среда, в которой распространяется упругая волна, представляется сплошной и непрерывной без учёта её дискретного или молекулярного строения.        Упругая волна называется продольной, если частицы среды колеблются в направлении распространения волны. Продольные волны связаны с объемной деформацией упругой среды и потому могут распространяться в любой среде - твердой, жидкой и газообразной, например - звук в воздухе. Упругая волна называется поперечной, если частицы среды колеблются, оставаясь в плоскостях, перпендикулярных к направлению распространения волн. Поперечные волны связаны с деформацией сдвига упругой среды и могут образовываться и распространяться только в средах, обладающих упругостью, т. е. в твердых телах. Поперечная волна - колебание струн музыкальных инструментов.

       Особое место занимают поверхностные волны, распространяющиеся вдоль свободной поверхности жидкости или поверхности раздела двух несмешивающихся жидкостей. В образовании и распространении этих волн определяющую роль играют силы поверхностного натяжения и тяжести.        При изменении объёма газа, вызываемое внешними воздействиями, вследствие упругих свойств этого газа происходит изменение его давления. Упругими свойствами обладают твёрдые, жидкие и газообразные тела. Упругими деформациями тел называют такие, которые после исчезновения внешних воздействий полностью восстанавливают свою первоначальную форму. Для упругих деформаций газов справедлив закон Гука, согласно которому элементарное dp приращение давления газа при малом изменении dV его объема прямо пропорционально относительной dV/V объемной деформации, вследствие чего имеет место следующее выражение:                                                                                                                                          dp = - kdV/V,     (2. 65)

где k - модуль объемной упругости газа. Знак " -" в (2. 65) указывает на то, что при положительном    dp приращении давления газа dV приращение объема отрицательно и наоборот. При очень медленном изменении объема газа процесс можно считать изотермическим, а при очень быстром - адиабатическим. В первом случае (4. 63) из раздела 4. 1 " Физическая термодинамика" модуль объемной упругости газа имеет значение: k = p, т. е равен в произвольный момент времени давлению газа, а во втором случае(4. 66) из раздела 4. 1 " Физическая термодинамика" модуль объемной упругости газа имеет значение: k = γ p, где γ - показатель адиабаты газа.

       Звуковыми или акустическими волнами называются упругие волны малой интенсивности, т. е. слабые механические возмущения, распространяющиеся в упругой среде. Звуковые волны, воздействуя на органы слуха человека, способны вызвать звуковые ощущения, т. е. слышимые звуки, если ν частоты соответствующих им колебаний лежат в пределах 16 - 2· 10⁴Гц. Упругие волны с частотами ν < 16 Гц называются инфразвуком, а с частотами ν > 2· 10⁴Гц - ультразвуком. Часто упругие волны с частотами ν > 10 ⁹Гц называют гиперзвуком. Распространение упругих волн в среде не связано с переносом вещества. В неограниченной среде оно состоит в вовлечении в вынужденные колебания все более и более удаленных от источника волн частей среды. Некоторый перенос вещества может осуществляться при распространении в среде сильных возмущений, например, ударных волн, возникающих при взрыве, когда колебания частиц среды становятся нелинейными.

       Среда называется однородной, если её физические свойства при неизменных условиях и существенных в рассматриваемых задачах, не изменяются от точки к точке. Среда называется изотропной, если её физические свойства, существенные в рассматриваемых задачах, одинаковы во всех направлениях. Среда называется линейной, если между величинами, характеризующими рассматриваемое внешнее воздействие на среду, существует прямо пропорциональная связь. Например, упругая среда, подчиняющаяся закону Гука, линейна по своим механическим свойствам. Бегущими волнами называются волны, которые в отличие от стоячих волн, переносят энергию в пространстве.



    Уравнение синусоидальной бегущей плоской и сферической волн, длина волны,                                                         фазовая скорость

       Механические возмущения или деформации распространяются в упругой среде с конечной       v скоростью. Поэтому возмущение, вызываемое источником волны в начальный момент t₀ времени и приводящее к смещению частиц упругой среды на максимальное A отклонение от положения равновесия достигает с запаздыванием на промежуток τ время M точек пространства, расположенных в плоскости равных фаз и находящихся от начала координат на y расстоянии. Плоскостью равных фаз или волновой поверхностью или фронтом волны называется геометрическое место точек, в которых фаза колебаний имеет одно и то же значение. Волновая поверхность отделяет возмущённую область упругой среды, в которой частицы этой среды вовлечены в волновой процесс, от невозмущённой области, в которой частицы упругой среды находятся в равновесном состоянии.     Волна называется плоской, если её волновые поверхности представляют совокупность плоскостей, параллельных друг другу. В плоской волне, распространяющейся вдоль OY оси, все          s величины, характеризующие смещение точек среды относительно положения равновесия в процессе колебательного движения, зависят от t времении y координаты рассматриваемой точки среды.

       На рис. 2. 16 в начальный момент t₀ = 0 времени И источник, находящийся в плоскости, проходящей через OO начало координат, создаёт в упругой среде плоский волновой фронт, т. е. все частицы, находящиеся в Пл. 1 плоскости равных фаз имеют одинаковые отклонения относительноположения равновесия, равные A амплитуде колебаний.

       Если И источник создаёт гармонические колебания в Пл. 1 плоскости равных фаз, которая в момент   t₀ = 0 временинаходится в начале OO координат, то зависимость s=s(t) отклонения колеблющихся частицот положения равновесия в Пл. 1 плоскости равных фаз произвольный момент t времени подчиняется (2. 28) уравнению: s =A cos(ω t+ φ ₀), где ω – циклическая частотагармонических



t₀ = 0

колебаний, создаваемых Иисточником.                    Если φ ₀начальная фаза колебаний частиц упругой среды(рис. 2. 16) в начальный момент    t₀ = 0 времени равна нулю, т. е. φ ₀= 0, то s₀максимальное отклонение этих частиц упругой средыот положения равновесия равно A амплитудеколебаний, вследствие чего это s₀максимальное отклонение имеет следующий вид:                                                    s₀ = Acosω t₀ = A.           (2. 66) В момент (рис. 2. 17) времени t₁ = T/4, где T - период колебаний И источника плоского



⇐ Предыдущая 123 4 5 6 7 Следующая ⇒