Проекция II закона Ньютонана OZ ось для m массы материала гибкого шнура ρп погонной 1 страница

волнового фронта, в OO начале координат частицы упругой средысогласно (2. 8) уравнению будут находиться в положении равновесия, т. е. sотклонения колеблющихсячастицот положения равновесия будут равны 0. По упругой средев положительном(рис. 2. 17)направлении OY оси к моменту t1 = T/4 времени A максимальное отклонение частицот положения равновесиядойдёт в направлении k волнового вектора, направленного в положительную сторону OY оси, с фазовой

v скоростью до Пл. 2 плоскости, проходящей через MM прямую и отстоящей от OO начала координат на y₁ = λ /4 расстоянии, где λ - длина плоской бегущей волны. Отклонение s₁от положения равновесия в Пл. 2 плоскости, проходящей через MM прямую, с учетом τ = T/4 временного запаздывания, за которое плоская бегущая волна распространяется от И источника до этой

Пл. 2 плоскости, согласно (2. 66) имеет следующее значение: s₁ = Acosω ( t₁- τ ) = A cosω (t₁- T/4) = A, (2. 67) где t₁ = T/4 - момент времени, отсчитанное от начального t₀ = 0 времени. Ещё через три четверти 3T/4 периода колебаний И источника плоского волнового фронта, т. е. к моменту t₂ = T времени, максимальное A отклонение частиц от положения равновесия дойдёт в направлении k волнового вектора, направленного в положительную сторону OY оси, с фазовой v скоростью до Пл. 2 плоскости, отстоящей от OO начала координат на расстоянии y₂ = λ . При этом И источник плоского волнового фронта вернётся в первоначальное состояние, в котором он находился в момент t₀ = 0 времени, т. е совершит один период T своих колебаний. Таким образом, плоский волновой фронт или плоская волна, находящаяся в начальный момент t₀ = 0 времени (рис. 2. 16), (рис. 2. 17) вПл. 1 плоскости, за Δ t = T промежуток времени распространитсяна расстояние, равноеλ длине волны. Согласно (рис. 2. 2) представлению колебаний векторными диаграммами одному периоду T гармонических колебаний И источника(рис. 2. 16) плоской волны соответствует поворот вектора A с модулём, равным амплитуде гармонических колебаний этого

И источника плоской волны, на 2π угол. За время T периода гармонических колебаний И источника плоская волна распространитсяв упругой среде на расстояние от этого И источника, равноеλ длине плоской волны. За время распространения плоской волны на λ расстояниеИ источник гармонических колебаний изменит фазу своих колебаний на угол 2π . Поэтому частицы упругой среды, имеющие расстояние между собой, равное λ длине волны, имеют различие по фазе колебаний этих частиц, равное 2π . Фазовая v скорость волны численно равна расстоянию, на которое перемещается Пл плоскостьравных фаз этой волны за единицу времени, вследствие чего выражение для определения фазовой v скорости имеет следующий вид: v = λ /T. (2. 68) где λ - расстояние, численно равное длине волны, которое плоская волна преодолевает с фазовой v скоростью за промежуток времени, численно равный T периоду гармонических колебаний И источникаэтой плоской волной.

В произвольный момент t времени плоская волна будет находиться на y расстоянии от начала координат, в которое придет с τ = y/v временным запаздыванием, где v - фазовая скорость перемещения (2. 68) в (рис. 2. 17) направлении k волнового вектора, перпендикулярного Пл. 2 плоскому волновому фронту и направленного в положительную сторону OY оси. Вследствие этого

s=s(t) отклонение от положения равновесия частиц упругой среды в произвольный момент t времени, т. е. уравнение распространяющейся в положительную сторону OY оси плоской синусоидальной волны, с учетом (2. 67) имеет следующий вид:

s = A cos[ω (t - τ )+ φ ₀] = A cos[ω (t - y/v)+ φ ₀] = Acos[ω t - (ω y/v) + φ ₀] = Acos(ω t - ky + φ ₀), (2. 69) где y - координата упругой среды, в которой определяется s=s(t) отклонение; φ ₀- начальная (2. 8) фаза колебаний частиц упругой среды в Пл. 1 плоскости с y = 0 координатой, т. е. в Пл. 1 плоскости равных фаз, где находится (рис. 2. 16) И источник гармонических колебаний, в начальный момент

t₀ = 0 времени; k = ω /v - волновое число, равное модулю k волнового k вектора, перпендикулярного (рис. 2. 17) плоскому Пл. 2 волновому фронту и направленного в положительную сторону OY оси в упругой среде.

С учетом выраженияω = 2π ν = 2π /T циклической или круговой частоты периодических колебаний из параграфа " Кинематика гармонических колебаний ", где ν - частота гармонических колебаний, создаваемых И источником (рис. 2. 16) в упругой среде, волновое k число (2. 69) принимает следующий вид: k = ω /v = 2π /vT = 2π /λ . (2. 70) где λ = vT - расстояние(2. 68), численно равное длине волны, которое плоская волна преодолеваетс фазовой v скоростью за промежуток времени, численно равный T периоду гармонических колебаний И источникаэтой плоской волной.

Величина (2. 69) Ф₁ = ω (t - y/v)+ φ ₀= ω t - ky+ φ ₀ равна фазовому углу, который имеют частицы упругой среды, находящиеся на y расстоянии от И источника гармонических колебаний, при своём отклонении от положения равновесия в данный момент t времени. Эта Ф₁ величина называется фазой волны, распространяющейся в положительном (рис. 02. 0. 17)направлении OY оси. Вдоль отрицательного (рис. 2. 17)направления OY оси в момент t₁ = T/4 времени частицы упругой среды, находящиеся на y = λ /4 расстоянии от И источника гармонических колебаний в Пл. 3 плоскостиравных фаз будут иметь отклонение от положения равновесия, равноеA амплитуде, но в противоположную сторону по сравнению с отклонениями частиц упругой среды в Пл. 2 плоскостиравных фаз положительного направления OY оси. Источник И гармонических колебаний фаз в момент t₁ = T/4 временибудет иметь (рис. 2. 2) фазовый угол, равный π /2, а частицы упругой среды в Пл. 3 плоскости равных фаз будут находиться в фазе π , опережающей фазовый угол этого источника на угол π /2. Поэтому при распространении волны вдоль отрицательного

(рис. 2. 17)направления OY оси величина (2. 69) ky, зависящая от расстояния Пл. 3 плоскости равных фаз колебаний частиц до И источника, будет определять опережение Ф₂ фазы волны по сравнению с ω t + φ ₀ фазой гармонических колебаний И источника. Фаза Ф₂ волны в случае её распространения в отрицательном (рис. 2. 17)направления OY оси в произвольный момент t времени будет иметь следующий вид: Ф₂ = ω t + ky+ φ ₀. (2. 71) Уравнение распространяющейся в отрицательную сторону OY оси плоской синусоидальной волны, т. е. s=s(t) зависимость отклонения от положения равновесия частиц упругой среды в произвольный момент tвремени, распространяющейся вдоль отрицательного направления OY оси, по аналогии с (2. 69) и с учётом (2. 70) будет иметь следующий вид: s = A cos(ω t + ky+ φ ₀), (2. 72) где y – имеет положительное численное значение и равняется расстоянию от 0 начала координат по OY оси до волнового фронта плоской синусоидальной волны, распространяющейся вдоль отрицательного направления OY оси в произвольный момент t времени. Фазы Ф₁ (2. 69) и Ф₂ (2. 71) упругих волн величиныпостоянные при распространении соответственно в положительном и отрицательном направлениях по OY оси в плоскости равных фаз. Поэтому для волнового фронта плоской синусоидальной волны зависимость Ф₁ фазы (2. 69)и Ф₂ (2. 71)этой волны от y координаты колеблющихся частиц упругой среды, начальной φ ₀(2. 70) фазы колебаний частиц упругой среды имеет следующий вид: Ф₂_{, 1}= ω t ± ky + φ ₀= const. (2. 73) где знаки " +", " -" указывают на распространение плоской синусоидальной волны в упругой среде соответственно в отрицательном и положительном направлениях по OY оси. Возьмём первую производную по t времени от левой и правой частей (2. 74) выражения вследствие чего выражение для определения фазовой v скорости имеет следующий вид:

dФ₂_{, 1}/dt = d(ω t)/dt ± d(ky)/dt + d(φ ₀)/dt ↔ 0 = ω ± kdy/dt = 0 ↔ dy/dt = ± ω /k. (2. 74) С учётом равенства первой производной от y координаты волнового фронта плоской синусоидальной волны по t времени фазовой v скорости перемещенияэтого волнового фронта в направлении (рис. 02. 0. 17 ) k волнового вектора, т. е. dy/dt=v, выражение (2. 74) принимает следующий вид: v = ± ω /k, (2. 75) где ω - циклическая частота гармонических колебаний (рис. 2. 16) И источника, вследствие чего в упругой среде возникаетволна; k - волновое число, равное k модулю k волнового вектора, направленного (рис. 2. 17 ) по OY оси, тогда в правой части (2. 76) выражения ставится " +" знак, и направленного (рис. 2. 17 ) противоположно OY оси, тогда в правой части (2. 76) выражения ставится

" -" знак.

Волна называется сферической, если её волновые поверхности имеют вид концентрических сфер. Центр этих сфер называется центром волны. Сферические волны возбуждаются в однородной изотропной среде уединенным точечным источником. Уравнение расходящейся сферической волны, т. е. зависимость s=s(t) отклонений частиц упругой среды от положения равновесия в произвольный момент t времени в функции r радиуса сферической волновой поверхности в этой упругой среде имеет следующий вид: s = (a₀/r)cos(ω t - kr + φ ₀), (2. 76) где a₀/r - амплитуда колебаний частиц упругой среды, уменьшающаяся при удалении на r расстояние от центра источника или возбудителя сферической волны; a₀ - физическая величина, численно равная амплитуде волны на единичном расстоянии от её центра; φ ₀ - начальная фаза колебаний в центре волны, а Ф = ω t - kr + φ ₀ - фаза сферической волны.

Звуковые волны в газах

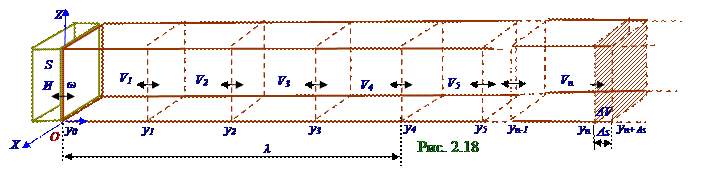
Звуковая волна в газе представляет собой распространяющуюся, например (рис. 2. 18) в трубе квадратного сечения, последовательность чередующихся областей сжатия и расширения газа, т. е. продольную волну. Поэтому давление в каждой точке пространства испытывает периодически изменяющееся Δ P отклонение от P среднего значения, совпадающего с давлением, которое существует в газе в отсутствие волн.

Вследствие колебаний c (2. 3) T = 2π /ω периодом гармонических колебаний (рис. 2. 18) внешнего И источника звука, например, мембраны, в длинном параллелипипеде V₁объем газа, находящийся между сечениями газа с y₀, y₁координатами, в интервал (рис. 2. 19) времени от 0 до T/4 испытывает сжатие ( штриховка

), вследствие чего область газаc y₀координатой и S площадьюпоперечного сечения переместится в y₀ + s_m положение, т. е. в положение своего максимального отклоненияот положения равновесия и одновременно в этой области газамежду сечениями газа с y₀, y₁координатами и S площадью

Мгновенное P^′ значение давления в некоторой точке пространства имеет следующий вид: P^′ = P + Δ P. (2. 77)

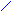
поперечного сечения переместится в y₀ + s_m положение, т. е. в положение своего максимального отклонения от положения равновесия и одновременно в этой области газа между сечениями газа с y₀, y₁координатами и S площадьюпоперечного сечения давление (2. 77)достигнет своего P^′_max максимального значения.

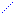
Молекулы газа, приблизившись друг к другу, после T/4 момента времени начнут отталкиваться друг от друга, вследствие чего V₁объем газа в интервал времени от T/4 до T/2 испытывает растяжение (штриховка ) и приведет из-за наличия упругих сил к сжатию (штриховка ) соседнего V₂ объёма, находящегося между сечениями газа с y₁, y₂координатами и т. д.

К моменту T времени сжатие газа дойдёт до сечения с y₄координатой. К этому же T времени в сечении газ с y₀координатой примет (рис. 2. 19) первоначальное состояние, какое он имел в момент t₀ = 0 времени, т. е. фаза колебаний частиц упругой среды в сечении с y₀координатой будет опережать по фазе колебания частиц упругой среды в сечении с y₄координатой на угол 2π . Согласно определению λ длины волны, по которому λ длина волны равна расстоянию между двумя ближайшими точками упругой среды, в которых разность фаз колебаний равна 2π , расстояние между сечениями газа с y₁, y₄координатами (рис. 2. 19) равно λ длине волны. Это λ расстояние продольная волна сжатия и расширения газа пройдет за T время с (2. 68) фазовой v скоростью распространения волны в направлении k волнового вектора, перпендикулярного плоской волновой поверхности S площадью (рис. 2. 18) поперечного сечения области газа.

Пусть в произвольный момент t времени (рис. 2. 18) в сечении с y_n координатой V_n объём газа испытывает расширение на Δ V величину, вследствие чего его правая грань с y_n₊₁ координатой сместилась относительно своего положения равновесия на Δ s расстояние.

На рис. 2. 20 изображено отдельно от всего газа в (рис. 2. 18) длинном параллелипипеде это приращение Δ V объёма газа. Расширение газа, т. е. положительное приращение Δ V объёма газа будет в том случае, если проекция F ^' _yn на OY ось вектора F^′ _yn силы давления газа, направленного перпендикулярно левой грани S площадью, по абсолютной величине будет больше проекция F ^' _{yn+ Δ}_s на OY ось вектора F результирующей силы на Δ V объёма газа будет иметь следующее положительное значение: - (|F ^' _{yn+ Δ}_s| - |F ^' _yn |) = - (|P'_{yn+ Δ}_s | -| P^′_yn| )S = F_y, (2. 78) где знак " -" минус перед разностью абсолютных величин (|F ^' _{yn+ Δ}_s| - |F ^' _yn|) проекцийсоответственно на левую и правую грани S площадью приращения Δ V объёма газа введён для получения

положительного значения проекцияF_y на OY осьвектора F результирующей силы ввиду того, что абсолютная величинапроекции F ^' _yn на OY осьвектора F^′_n силы давления на левую грань S площадью по абсолютной величине будет больше проекции F ^' _{yn+ Δ}_s на OY осьвектора F^' _{yn+ Δ}_s силы давления на правую грань той жеS площадью.

В выражении (2. 78) произведения P^′_yn, P^′_{yn+ Δ}_s давлений газасоответственнона левую и правую грани (рис. 2. 20) Δ V объёма газа S площадьюэтихгранейравны F ^' _yn, F ^' _{yn+ Δ}_s проекциям на OY ось

векторов F^' _yn, F^' _{yn+ Δ}_s, т. к. векторы F^' _yn, F^' _{yn+ Δ}_s сил давления газа перпендикулярны граням Δ V объёма газа, а OY ось координат тоже перпендикулярна граням S площадью Δ V объёма газа.

Приращение (2. 78)Δ P′ = (|P' _{yn+ Δ}_s| -|P^′_yn|) давления в Δ V объёме газа на (рис. 2. 20) Δ s длине имеет вид: Δ P′ = (∂ P^′/∂ y)Δ s, вследствие чего проекцияF_y на OY осьвектора F результирующей силы, действующей на Δ V объём газа S площадью и Δ s длиной, имеет следующий вид: F_y = - (∂ P^′/∂ y)Δ sS. (2. 79)

Проекция II закона Ньютонана OY осьдля m массы газа ρ плотностью, заключённой в приращении(рис. 2. 20) объема Δ V=SΔ s, к которой по OY оси приложена F_yсилаи имеющей по этой оси проекцию ∂ ²s/∂ t² вектора ускорения, с учётом (2. 79) имеет следующий вид: OY: ρ SΔ s(∂ ²s/∂ t²) = F_y ↔ ρ SΔ s(∂ ²s/∂ t²) = - (∂ P^′/∂ y)Δ s S ↔ ↔ ρ (∂ ²s/∂ t²) = - ∂ P^′/∂ y, (2. 80) т. е. проекция ∂ ²s/∂ t² на OY осьвектора ускорения Δ Vобъёма газапропорциональна∂ P^′/∂ y первой производной давления в этом Δ Vобъёме газа, испытывающего в результате распространениязвуковой волныв газе сжатиеили расширение.

Волновое уравнение распространения акустических волн в однородной изотропной непоглощающей упругой среде: фазовая скорость распространения звука

В звуковой волне сжатие и расширение газа следуют друг за другом через короткие промежутки времени, вследствие чего смежные участки упругой среды не успевают обмениваться теплом. Поэтому связь между P давлением и V объемом соседних участков газа, в котором распространяется акустическая волна, определяется законом Пуассона (4. 68) из раздела 4. 1 " Физическая термодинамика", имеющего следующий вид: PV^γ = const, (2. 81) где γ - отношение молярнойC_p теплоемкости газапри постоянном Pдавлении к молярной

C_v теплоемкости газа при постоянном V объеме. Уравнение (2. 81) Пуассона для двух состояний газа: до возникновения упругой волны в газе с давлением (рис. 2. 18) в V_n объеме и после возникновения волны в газе, вследствие чего в

V_n + Δ V = S(Δ y + Δ s) объеме давление этого газа стало равным P ^′ , имеет следующий вид:

P(SΔ y)^γ = P ^′ [S(Δ y + Δ s)]^γ = P ^′ {S[Δ y + (∂ s/∂ y)Δ y]}^γ = P ^′ (SΔ y)^γ [1 + (∂ s/∂ y)]^γ ↔ ↔ P ^′ = P/[1 + (∂ s/∂ y)]^γ ≈ P/[1 +γ (∂ s/∂ y)] ≈ P[1 -γ (∂ s/∂ y)], (2. 82) где Δ y - длина (рис. 02. 0. 18) V_nобъёма между сечениямис y_n и y_n₊₁координатами.

⇐ Предыдущая 1 234 5 6 7 Следующая ⇒