С)кездейсоқ шамалардың сандық сипаттамалары.

С)кездейсоқ шамалардың сандық сипаттамалары.

Анықтама. Кездейсоқ шаманың барлық мүмкін мәндерін сәйкес ықтималдықтарына көбейтіп қосқаннан шыққан санды кездейсоқ шаманың математикалық күтімі деп атайды да, M(x) деп белгілейді.

M(x)=x₁p₁+x₂p₂+…+x_np_n

Математикалық күтімнің мынадай қасиеттері бар:

1-қасиет. Тұрақты шаманың математикалық күтімі сол шаманың өзіне тең. M(C)=C.

2-қасиет.Тұрақты шаманы математикалық күтім таңбасы алдына шығаруға болады. M(C*X)=C*M(X).

3-қасиет.Екі кездейсоқ шама қосындысының математикалық

Күтімі олардың математикалық күтімнің қосындысына тең.

M(X+Y)=M(X)+M(Y).

4-қасиет.Тәуелсіз екі кездейсоқ шама көбейтіндісінің математикалық күтімі олардың математикалық күтімдерінің көбейтіндісіне тең. M(X*Y)=M(X)*M(Y).

5-қасиет.Кездейсоқ шаманың математикалық күтімнен ауытқуының математикалық күтімі нөлге тең. M(X-M(X))=0.

Анықтама.Кездейсоқ шаманың математикалық күтімнен ауытқуы квадратының математикалық күтімін дисперсия деп атайды да, D(X) деп белгілейді:

D(X)=M[{X-M(X)}²].

Теорема.X кездейсоқ шаманың дисперсиясы X²кездейсоқ шаманың математикалық күтімі мен X кездейсоқ шаманың математикалық күтімі квадратының айырымына тең.

D(X)=M(X²)-[M(X)]².

Дисперсияның бірнеше қасиеттерін келтірейік:

1-қасиет.Тұрақты шаманың дисперсиясы нөлге тең D(C)=0.

2-қасиет.Тұрақты шаманы дисперсия таңбасы алдына квадраттап алып шығаруға болады D(C*X)=C²*M(X).

3-қасиет.Екі кездейсоқ шама қосындысының диспесиясы олардың дисперсияларының қосындысына тең

D(X+Y)=D(X)+D(Y).

4-қасиет.Екі кездейсоқшама айырымының дисперсиясы олардың дисперсияларының қосындысына тең

D(X-Y)= D(X)+D(Y). Анықтама.Кездейсоқ шама дисперсиясынан алынған квадрат түбір орта квадраттық ауытқу деп аталады да,σ(X) деп белгіленеді: σ(X)= 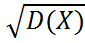. Орта квадраттық ауытқу дисперсияның квадрат түбірі болғандықтан, оның өлшемі сызықты болады, яғни кедейсоқ шама өлшемімен бірдей. Орташа квадраттық ауытқуда кездейсоқ шама қабылдайтын мәндерінің математикалық күтімнен қаншалықты шашыраңқы орналасқанын көрсетеді.

⇐ Предыдущая 6 7 8 9 10 11 121314 15 Следующая ⇒