b)Тәуелсіз және тәуелді оқиғалар.

b)Тәуелсіз және тәуелді оқиғалар.

Егер екі оқиғаның бірінің пайда болуы екіншісінің пайда болу ықтималдығын өзгертпесе, ондай екі оқиғаны тәуелсіз деп атайды.Егер екі оқиғаның бірінің пайда болуы екіншісінің пайда болу ықтималдығын өзгертетін болса, ондай оқиғаны тәуелді оқиғалар деп атайды.А оқиғасының пайда болуы В оқиғасының пайда болуына байланысты, яғни А оқиғасының пайда болу ықтималдығы Воқиғасының пайда болуына байланысты өзгереді. Мұндай ықтималдықты шартты ықтималдық деп атайды. Шартты ықтималдықты былай белгілейді: 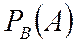- В оқиғасы орындалғанда А оқиғасының пайда болу ықтималдығы.

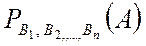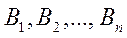- оқиғалары орындалғанда А оқиғасының пайда болу ықтималдығы.

c)Толық ықтималдық

Айталық, Н₁, Н₂, ...,Н_п оқиғалары қос-қостан үйлесімсіз оқиғалардың толық тобын құрайтын болсын. Ал В оқиғасы осы оқиғалардың тек біреуімен ғана бірігіп орындалады дейік. Оның үстіне р(Н₁), р(Н₂), ...,р(Н_п) және 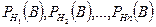ықтималдықтары белгілі болсын. ықтималдықтың толық формуласы Шынында 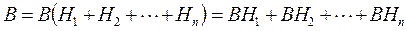(1)Ал Н₁, Н₂, ...,Н_п қос-қостан үйлесімсіз болғандықтан, 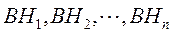оқиғалары да қос-қостан үйлесімсіз. Олай болса, бұл оқиғаларға қосу теоремасын қолдануға болады. Сонда

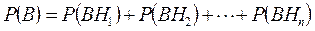шығады.

Көбейту теоремасы бойынша

болады.

Демек,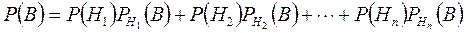

немесе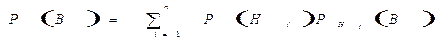

жоғарыдағы берілгендері бойынша В-нің ықтималдығын осы (2) формуламен анықтайды. Бұл формуланы ықтималдықтардың толық формуласы деп атайды. Әдетте, Н₁, Н₂, ...,Н_п оқиғаларын гипотезалар (болжамдар) деп атайды.

Байес формуласы.Осы уақытқа дейін қарастырып келген ықтималдықтар интуитивті түрде теориялық болжамдарға сүйеніп, тәжірибе жүргізбей-ақ, комплекс шарт жөніндегі білім (түсінік) негізінде анықталып келді. Тәжірибеге дейінгі Н₁, Н₂, ...,Н_п гипотезалар (оқиғалар) ықтималдығы сәйкес түрде р(Н₁), р(Н₂), ...,р(Н_п) болатынды.

Тәжірибе жүргізілді делік, соның нәтижесінде В оқиғасының пайда болғаны анықталды, енді осы В оқиғасының пайда болуына байланысты Н₁, Н₂, ...,Н_п гипотезаларының ықтималдығын қайта қарауға тура келеді. Яғни 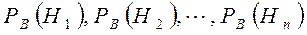ықтималдықтар мәнін анықтауға тіреледі. Бұл ықтималдықты анықтау үшін, көбейту теоремасы мен ықтималдықтардың толық формуласын пайдаланамыз.

Тәуелді оқиғалар В ме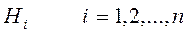н үшін

Бұдан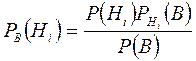

шығады. Бұл формулаға толық ықтималдық формуласынан 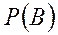мәнін қойсақ, онда

шығады. Осы (3) формуланы Байес формуласы деп айтады.P(H_i) ықтималдықтары гипотезалардың априорлы (тәжірибеге дейінгі) ықтималдықтары,ал P_B(H_i)-апостериорлы (тәжірибеден кейінгі) ықтималдықтары деп аталады.

18.Қайталанбалы тәуелсіз сынақтар. Бернули формуласы. Тәуелсіз п рет тәжірибе жасадық дейік. Әр жолы ізделінді А оқиғаның пайда болу ықтималдығы тұрақты 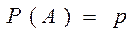болсын. Онда А оқиғасының пайда болмауы 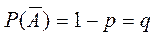болады. Енді осы тәжірибелер нәтижесінде А оқиғасы k рет пайда болу ықтималдығын 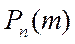деп белгілейді және ол мынаған тең:

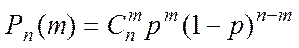
Осы формуланы Бернулли формуласы деп атайды.

Муавр-Лапластың шектік теориясыТеория-1. Айталық 0<p<1 болсын. Онда |k-np|=o((npq 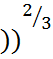шартын қанағаттандыратын барлық к-лар үшін бірқалыпты түрде

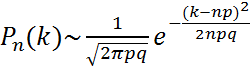, n

Яғни n кезде sup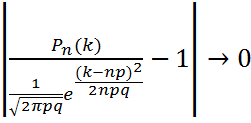

{k;|k-np|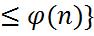

Мұндағы 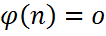((npq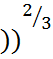

Теореманы дәлелдемес бұрын мынаған назар аударайык: егер

функциясын және 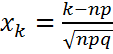белгілеуін енгізсек, онда теореманы былай тұжырымдауға болады.

1`-теорема. 0<p<1 болсын . онда барлық 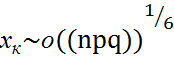үшін

Лапластың интегралдық теоремасы тәуелсіз n рет тәжірибе жасағанда ізделінді А оқиғаның пайда болу ықтималдығы тұрақты Р(А)=p болсын. Онда А оқиғасының пайда болу саны 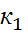мен 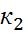арасында болу ықтималдығы P_n(k₁,k₂) жуық шамамен мынаған тең:

P_n(k_1,k₂)≈Ф(х₂) – Ф(х₁) мұндағы

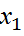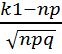Ф(х)= және = x₂=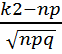

N артқан сайын муавр-лаплас формуласына мәні дәлірек болады және бұл формуланы npq 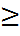20 болған кезде қолданған жөн. Есептеуді оңайлату үшін ықтималдылықтар теориясы оқулықтарында Ф(х)= функциясының кестесі беріледі.бұл функция тақ яғни f(-x)= - f(x), және х артқан сайын функция 1-ге ұмтылады. (х>4 болған кезден бастап 1-ге тең функция деп есептеуге болады)

⇐ Предыдущая 6 7 8 9 101112 13 14 15 Следующая ⇒