P - σP/σx ½ dx) dy dz – (P+ σP/σx ½ dx) dy dz + Fxρ dx dy dz = 0

(P - σP/σx ½ dx) dy dz – (P+ σP/σx ½ dx) dy dz + Fxρ dx dy dz = 0

Разделим почленно данное уравнения (т.е. приведем каждый члем к единице массы) на dm = ρ dx dy dz и получим:

Fx – 1/ ρ σP/σx = 0

1/ρ σP/σx –единичная поверхностная сила, σP/σx –градиент изменения давления.

Очевидно, что для любого избранного направления:

Fн – 1/ρ σP/σx = 0

Можем записать систему уравнений, которая называется общим условием равновесия жидкости:

Fx – 1/ρ σP/σx = 0 dx

Fy – 1/ρ σP/σx = 0 dy

Fz – 1/ρ σP/σx = 0 dz

Получена эта система в1755 году членом Российской академии наук Леонардом Эймром.

Умножим полученые уравнения на dx dy dz и сложив их получим:

Fx dx + Fy dy + Fz dz = 1/ρ (σP/σx dx + σP/σx dy + σP/σx dz)

Т.к. Р = φ (х, у, z),то выражение в скобках справа представляет собой полный дифференциал давления:

dP = ρ(Fx dx + Fy dy + Fz dz)

Это уравнение называют дифференциальным уравнением равновесия жидкости.

Физический смысл этого уравнения: поверхностные силы равны массовым.

Поверхность равного давления.

Поверхностью равного давления в жидкости называется поверхность, все точки которой испытывают равное давление.

Уравнение такой поверхности мы можем получить из основного уравнения равновесия жидкости, полагая P=constили dP = 0

Поверхность уровня на границе жидкой и газообразной сред называется свободной поверхностью.

Положение свободной поверхности зависит от сил, действующих на жидкость.

Свободная поверхность покоящийся жидкости

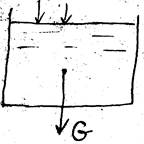
Из всех объемных сил на жидкость действует только вес, тогда F_x = 0 ; F_y = 0; F_z = 0

Дифференциальное уравнение будет представлено в виде: