P = lim ΔΦ/ΔS – гидростатическое давление в точке при ΔS → 0

Рср = Φ/S

Р_ср – называется средним гидростатическим давлением

Р = ΔΦ/ΔS – напряжение

P = lim ΔΦ/ΔS – гидростатическое давление в точке при ΔS → 0

Размерность давления в [ Н/м², Па ]. Окружающий нас воздух действует на нас давлением, которое называют атмосферным:

Р_атм= 1т._атм = 9,81 Н/см² = 98100 Н/см²[Па] = 98,1 кН/м² [кПа]

Свойства гидростатического давления.

Давление в точке обладает тремя свойствами:

1. Гидростатическое давление в точке действует нормально к площади его воспринимающей и являющееся сжимающим, т.е. оно направленно внутрь того объема жидкости, давление на который мы рассматриваем.

В движущейся жидкости при наличии касательных напряжений возникла бы необходимость доказывать это свойство. Здесь же ее нет.

2. Величина давления в рассматриваемой точке не зависит от ориентации площадки, т.е. как бы не располагалась площадка давление всегда направлено к ней нормально.

3. Гидростатическое давление в точке зависит от ее координат в пространстве. Это свойство специального доказательства не требует, т.к. ясно, что по мере погружения точки под уровень жидкости давление будет возрастать, и наоборот.

Р = φ (х, у, z)

Лекция №2

Дифференциальные уравнения равновесия

жидкости (ур. Эймра). Поверхности равного

давления. Основные уравнения и закон

гидростатики.

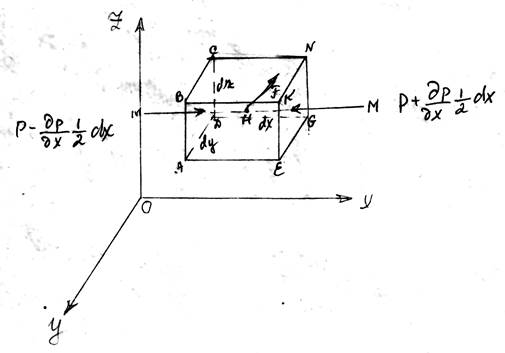
Выделим в жидкости, находящийся в равновесии, элементарный параллелепипед со сторонами dx, dy, dz и центром Н. Рассматриваемый объем находящийся в равновесии под воздействием:

- поверхностных сил давления, направленных внутрь параллелепипеда нормально к его граням;

- объемных (массовых) сил, действующих на каждую частицу жидкости.

Р – гидростатическое давление в т. Н. Учитывая непрерывность изменения давления в жидкой среде и пренебрегая величинами бесконечно малыми, стремящихся к нулю при уменьшении выделенного объема до размеров точки, определим среднее гидростатическое давление на соответствующих гранях; изменение величин давления, приходящихся на единицы длинны ММ представим частной производной σP/σx.

На грани АВСD действует давление: P - σP/σx ½ dx; на грани EKNG: P+ σP/σx ½ dx.

Сила давления определяется соответственно как произведение давления в центре тяжести на площадь действия этого давления.

Массовая сила dF=dm ^.j,проекция этой силы по координатным осям F_x, F_y, F_z; dm=ρ dx dy dz.

Составим уравнение равновесия в направлении оси ОХ, из которого следует, что проекция всех сил, действующих на выделенный объем, в направлении любой оси (например ОХ) равна 0:

⇐ Предыдущая 1 234 5 6 7 8 9 10 Следующая ⇒