lim Δm/ΔV при ΔV ---> 0

⇐ ПредыдущаяСтр 2 из 15Следующая ⇒

ρ = lim Δm/ΔV при ΔV ---> 0

2. Вес единицы объема жидкости (удельный вес или объемный вес)

r = G/V [H/м³]

Для однородной жидкости r есть отношение веса жидкости к ее объему.

Ньютон представляет собой силу, которая массе в 1 кг сообщает ускорение в 1 м/с² ; Н = кг ^.м / с²

Вес единицы объема при 4 ⁰С воды:

ρ = 9810 Н/м9 G = rV, а G = gm

g – ускорение свободного падения тела (ускорение силы тяжести)

rV = gm = ρgV, r =ρg, а ρ=r/g

3. Сжимаемость (или объемная упругость) жидкости.

Упругой сжимаемостью жидкости называется ее способность принимать свой прежний объем V после снятия внешней нагрузки.

В качестве меры упругого сжатия жидкости принимают величину:

К = - ΔPV/ΔV [ ]

К – называют модулем объемной упругости жидкости. Для воды К=22^.10⁵к Па ≈ 220 КН/м²

4. Расширение при повышении температуры – характеризуется коэффициентом температурного расширения β_t. Этот коэффициент показывает относительное изменение объема при увеличении температуры на один градус:

βt = 1/V . dV/dt

5. Вязкость – способность жидкости оказывать сопротивление скольжения одного ее слоя относительно другого.

Допусти, что жидкость занимает пространство между двумя горизонтальными пластинками, из которых нижняя неподвижна (U_н=0), а верхняя перемещается с постоянной скоростью U_в.

Через некоторое время частицы, ближе к верхней пластинке приобретают скорость большую, чем частицы удаленные от нее.

Разность скоростей движения слоев «а» и «в» равна:

du = U_a– U_в

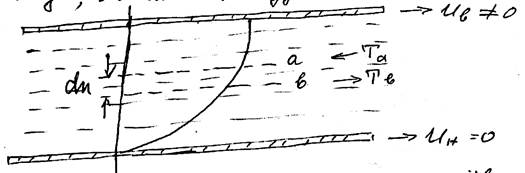
Между этими слоями возникают силы трения: Т_в – сила, ускоряющая движение слоя «в», а Т_а – сила, тормозящая перемещение слоя «а».

Т = ± МS du/dn или T/S = τ =± M du/dn,

где Т – сила трения; М – коэффициент динамической вязкости, т.е. коэффициент, характеризующий свойства данной жидкости; S – площадь поверхности соприкосновения слоев; du/dn – градиент скорости по нормам (du – скорость движения одного слоя относительно другого; а dn – расстояние между осями двух смежных слоев); τ – напряжение сил трения, возникающих на поверхности соприкосновения слоев. Знак + – принимают в зависимости от изменения градиента скорости.

Коэффициент динамической возможности, М равен:

М = Т/S ^.dn/du [H^.c/ м² или кг/м ^.с]

1 H ^. c/ м² = 10 n3; 1n3 = 0,1 H ^. c/ м²

Коэффициент М данной жидкости зависит от температуры.

Для расчетов часто принимают коэффициент кинематической вязкости ν,представляющий собой отношение коэффициента динамической вязкости к плотности жидкости:

ν = М/ρ [ H ^.м ^.с/кг или м²/с]

ν данной жидкости зависит от температуры.

Гидростатика. Силы действующие в жидкости.

Все силы действующие на частицы жидкости можно разделить на две группы: внешние силы и внутренние силы упругости.

Внутренними силами упругости называются силы взаимодействия между частицами жидкости.

Внешние силы – силы, приложенные к частицам рассматриваемого объема жидкости со стороны других тел, в частности со стороны жидкости, окружающей данный объем.

Внешние силы делятся на массовые и поверхностные.

1. Массовыми силами называются такие, величина которых пропорционально массе жидкости. Эти силы действуют на все частицы рассматриваемого объема жидкости.

При ρ = const, величина массовых сил пропорциональна объему жидкости, поэтому их можно назвать объемными.

К этим силам относится собственный вес жидкости и силы инерции.

2. Поверхностными силами называют такие, величина которых пропорциональна поверхности, на которую действуют эти силы. К числу таких сил относятся:

а) сила абсолютного давления, действующего на свободной поверхности;

б) силы трения.

Гидростатическое давление.

В гидростатике изучают жидкость, находящуюся в покое. Касательные напряжения в ней равны нулю. Считается также, что жидкость неспособна сопротивляться растягивающим усилиям. Поэтому будем считать, что в любой точке жидкости имеется только нормальное напряжение σ = σ_н

Гидростатическим давлением в данной точке называют скалярную величину, равную значению напряжения в рассматриваемой точке:

ρ = |σ|, где |σ| - значение напряжения

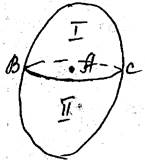Гидростатическое давление можно пояснить следующим образом. Возьмем произвольный объем жидкости, внутри которого отметим ^. А, через которую проведем произвольную поверхность ВС.

Эта поверхность расчет объем на две части I и II. Выделим у точки А на поверхности ВСплощадь S. На эту поверхность будет передаваться сила давление со стороны объема I на объем II.

Сила Φ, действующая на площадь S называется силой гидростатического давления. Сила объема I – внешняя поверхностная сила.

⇐ Предыдущая 123 4 5 6 7 8 9 10 Следующая ⇒