
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Расчеты на срез и смятие. Пример № 1. Решение.
Расчеты на срез и смятие
Пример № 1
Круглый стержень, растягиваемый силой F = 180 кН укреплен на детали с помощью чеки прямоугольного сечения (рис.1). Из условий прочности на растяжение, срез и смятие стали определить диаметр стержня d, необходимую длину а хвостовой его части, а также размеры поперечного сечения чеки t и h без учета ее работы на изгиб. Допускаемые напряжения принять: [σр] = 160 МПа, [τср] = 100 МПа, [σсм] = 320 МПа.
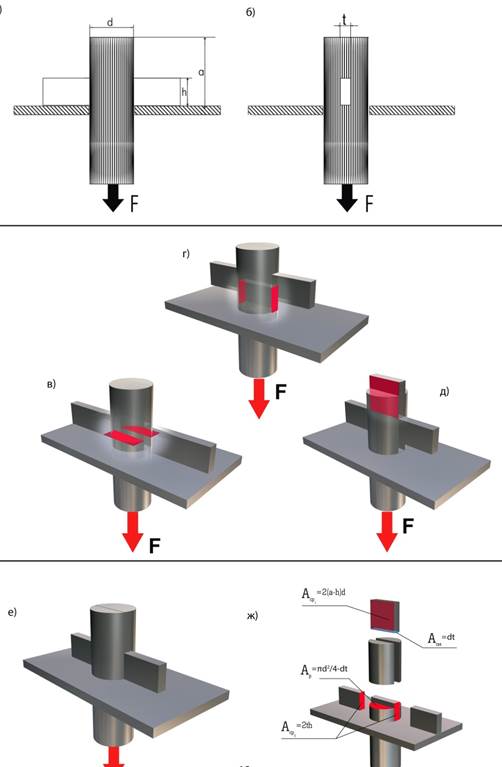
Рис.1
Решение.
Стержень под действием силы F испытывает растяжение, ослабленным сечением будет сечение стержня, которое проходит через чеку. Его площадь определяется как разность площадей круга и прямоугольника, у которого одна сторона равна ширине чеки t, а вторую можно принять равной диаметру стержня d. 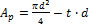 . Эта площадь показана на (рис. 1, ж).
. Эта площадь показана на (рис. 1, ж).
По условию прочности на растяжения
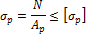
определяем площадь растяжения, подставляя N = F, имеем:
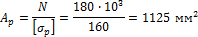
приравнивая 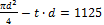 (1) получаем первое уравнение. В хвостовике стержня под давлением чеки может произойти срез по площади Аср = 2(a - h)∙d. Из условия прочности на срез
(1) получаем первое уравнение. В хвостовике стержня под давлением чеки может произойти срез по площади Аср = 2(a - h)∙d. Из условия прочности на срез

определим площадь среза хвостовика
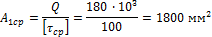
отсюда 2(a - h)·d = 1800 (2) получаем второе уравнение.
Исходя из условия равно прочности на срез стержня и чеки определяем площадь среза чеки, которая определяется как A2ср = 2h∙t и равны A1ср т.е. A2ср = A1ср, поэтому получаем третье уравнение 2h∙t = 1800 (3).
Под действием силы F чека, оказывая давление на внутреннюю часть стержня вызывает смятие стержня по площади Aсм = d·t. Из условия прочности на смятие
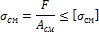
определяем площадь смятия:
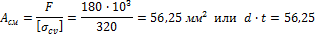
Таким образом, получим четыре уравнения для определения диаметра стержня d, длины хвостовика а и размеров поперечного сечения чеки t и h:
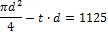
2(a - h)∙d = 1800 (4)
2h∙t = 1800
d∙t = 56,25
подставим в первое уравнение системы (4) вместо d∙t = 56,25, получим:
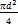 – 56,25 = 1125 или
– 56,25 = 1125 или 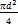 = 1125 + 56,25 = 1687,5
= 1125 + 56,25 = 1687,5
отсюда 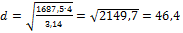 т.е. d=46,4мм
т.е. d=46,4мм
т.к. d∙t=56,25, 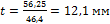 ; t = 12,1 мм.
; t = 12,1 мм.
Из третьего уравнения системы (4) определяем h.
2h∙t = 1800, отсюда 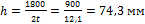 ; h = 74,3 мм.
; h = 74,3 мм.
Из второго уравнения системы (4) определяем а.
2(a - h)∙d = 1800
(a - h) = 900, отсюда
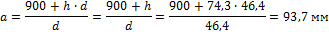
Итак, а = 93,7 мм.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|