Динамика.

10. Динамика.

Кинетодинамика (или просто динамика) изучает нестационарные неравновесные системы. Заряд частично пронизывает такие системы (W ¹ 0) и частично остается в них (DW ¹ 0). Критерий K_W имеет значения меньше единицы и больше нуля.

Мысленно выделив в системе элементарный объем dV и составив для него уравнение баланса заряда с помощью формул типа (37) и (42), после несложных преобразований найдем (поле потенциала одномерное)

U₁ = L₁₁Z₁ + L₁₂Z₂ ; (118)

U₂ = L₂₁Z₁ + L₂₂Z₂ , (118)

где

U₁ = rc_11P(dP₁/¶t) ; U₂ = rc_22P(dP₂/¶t) ; (119)

Z₁ = ¶²P₁/¶x² ; Z₂ = ¶²P₂/¶x² ; (120)

L₁₂ = L₂₁ ; (121)

c_11P и c_22P - удельные массовые емкости системы.

Если L₁₂ = L₂₁ = 0, то дифференциальные уравнения (118) динамики распадаются на простейшие независимые уравнения типа дифференциального уравнения теплопроводности Фурье, второго закона Фика и т.д.

Для системы с n степенями свободы и трехмерным полем потенциала дифференциальные уравнения динамики имеют вид

U_i = 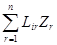(122)

где i = 1, 2, ... , n;

Z_r = (¶²P_r/¶x²) + (¶²P_r/¶y²) + (¶²P_r/¶z²) ; (123)

L_ir = L_ri (124)

Уравнения (118) и (122) могут найти широкое применение в самых различных областях науки и техники. В частности, при изучении химических и фазовых явлений для каждой подсистемы записываются уравнения типа (122) - они характеризуют процесс перераспределения зарядов в пределах данной подсистемы - и затем рассматривается процесс обмена зарядами между подсистемами, а также между системой в целом и окружающей средой (параграф 9). Для интегрирования получающейся совокупности уравнений целесообразно использовать электронно-вычислительные устройства.

Законам (118) и (122) подчиняются также процессы азотизации, цементации, нитроцементации, алитирования и т.д. Из уравнений (118) видно, что создание дополнительных градиентов (разностей) температуры, электрического потенциала, давления и т.д. позволяет существенно увеличить поток массы. Например, большой градиент температуры возникает, если тело поместить в электрическое поле высокой частоты. При этом на поверхности изделия из армко-железа, покрытого специальной пастой (состав в % по массе: красная кровяная соль -15, барий углекислый - 20, сажа голландская - 45, поташ - 20), образуется нитроцементованный слой толщиной до 0,3 мм за 30 сек (вместо нескольких часов по обычной технологии) [13].

Комплексный термодинамический анализ потоков тепла, фазовых и термических напряжений [с помощью закона упругости типа (78)] и т.д. позволил количественно оценить влияние граничных условий и установить, что с уменьшением площади поверхности соприкосновения металлической литейной формы (кокиля) и отливки до нуля термические и фазовые напряжения в форме также стремятся к нулю. На этой основе были созданы кокили, собираемые из нормализованных элементов (в том числе из отрезков проволоки - иголок). Игольчатые формы обладают податливостью и газопроницаемостью, они практически не коробятся, их стойкость возрастает в десятки и сотни раз по сравнению со сплошными. Впервые в мировой литейной практике был осуществлен процесс отливки тяжелых чугунных станин в соответствующую кокильную машину.

Аналогичным образом путем совместного анализа процессов затвердевания металла и кипения охлаждающей воды был разработан способ литья чугунных и стальных изделий в легкоплавкие алюминиевые кокили [16, 28]. Внедрение описанных методов на заводах дает сотни тысяч рублей годовой экономии.

¨ ¨ ¨

Изложенная выше общая феноменологическая теория физических и химических процессов (ее можно назвать также общей феноменологической теорией переноса) органически объединяет в себе классическую термодинамику, термодинамику Онзагера, теорию теплообмена, химическую кинетику и т.д. Главную роль в ней играют дифференциальные уравнения состояния, выраженные через обобщенные заряды и потенциалы.

В вопросе о границах применимости теории надо различать следующие два аспекта. Первый касается общих ограничений, налагаемых на любую феноменологическую теорию (размер системы должен быть достаточно велик по сравнению с размерами элементарных частиц и расстояниями между ними и т.д.). В частности, разность DР, взятая на пути Dх (среднее расстояние между молекулами, или средний свободный пробег), должна быть много меньше потенциала Р, т.е. должно соблюдаться условие

DР/Р «1. (125)

В этом смысле границы применимости общей теории нисколько не уже, чем границы применимости отдельных простейших законов (Ома, Фурье, Фика, Дарси и т.д.), на которые распадаются общие законы переноса (39) и (122) при отсутствии взаимного влияния степеней свободы.

Второй аспект проблемы касается частных ограничений, накладываемых на теорию конкретными специфическими особенностями изучаемого явления. Например, с изменением влажности капиллярнопористого тела изменяются формы связи влаги и материала, и соответственно меняется природа (конкретное аналитическое выражение) химического потенциала и т.п. [10, 13].

Немаловажное значение для теории имеет правильный учет всех имеющихся степеней свободы системы (неполный учет степеней свободы есть наиболее часто встречающийся источник возникающих погрешностей). В этом отношении важную роль приобретают отклонения системы от равновесного или стационарного состояния. Например, при химических и фазовых превращениях вблизи равновесного состояния наиболее существенной является химическая (или фазовая) степень свободы. В неравновесных условиях приходится учитывать также термическую, механическую, диффузионную, электрическую и другие степени свободы.

Вблизи равновесия перенос электрического заряда допустимо изучать без учета возникающего магнитного поля. В неравновесных условиях появляется дополнительная - магнитная - степень свободы и систему надо рассматривать как электромагнитную.

Если заряд обладает заметной массой (или сам представляет собой массу), то отклонение системы от стационарных условий приводит к появлению дополнительной инерционной степени свободы (связанной с действием ускорений) и т.п.

Литература.

1. L. Onsager. Reciprocal Relations in Irreversible Processes - I and II. Physical Review, 37, 405 and 38, 2265, 1931.

2. К. Д е н б и г. Термодинамика стационарных необратимых процессов. Перевод с англ. М., ИЛ, 1954.

3. С. Р. д е Гроот. Термодинамика необратимых процессов. Перевод с англ. М., ГИТТЛ, 1956.

4. D. Miller. Thermodynamic Theory of Irreversible Processes Amer, J. Phys., 24, N 6, 1956.

5. D. G. Miller. Thermodynamics of Irreversible Processes. The Experimental Verification of the Onsager Reciprocal Relations. Chemical Reviews, 60, N 1, 1960.

6. И. Пригожий. Введение в термодинамику необратимых процессов. Перевод с англ. М., ИИ Л, 1960.

7. М. Т г i b u s. Jnformation Theory as the Basis for Thermostatics and Thermodynamics. Trans. ASME. Ser. E. J. Appl. Mech., 28, N 1, 1961.

8. Термодинамика необратимых процессов. Лекции в летней международной школе физики им. Энрико Ферми. Перевод с англ. М., ИИ Л, 1962.

9. С. д е Гроот, П. М а з у р. Неравновесная термодинамика. Перевод с англ. М., изд-во «Мир», 1964.

10. А.И. Вейник. Термодинамика. Минск, изд-во МВСС и ПО БССР, 1961; изд. 2-е. Минск, изд-во «Высшая школа», 1965.

11. А.И. Вейник. Техническая термодинамика и основы теплопередачи. Изд. 2-е, М., изд-во «Металлургия», 1965.

12. А.И. Вейник. Об ошибочном понимании термодинамики. Известия высших учебных заведений «Энергетика», № 3, 1965.

13. А.И. Вейник. Термодинамика необратимых процессов. Минск, изд-во «Наука и техника», 1966.

14. Д ж. Робертс. Теплота и термодинамика. Перевод с англ. М.-Л., ГИТТЛ, 1950.

15. А.И. Вейник. Расчет структуры чугуна. Минск, изд-во «Высшая школа», 1964.

16. А.И. Вейник. Расчет отливки. М., изд-во «Машиностроение», 1964.

17. А.И. Вейник. Усадочные явления и питание отливок. Минск, изд-во «Высшая школа», 1964.

18. А.И. Вейник. Развитие теории теплоты. Вестник АН СССР, № 4, 1962.

19. Г. Голдсмид. Применения термоэлектричества. Перевод с англ. М., ГИФМЛ, 1963.

20. П.С. Эпштейн. Курс термодинамики. Перевод с англ. М.-Л., ОГИЗ ГИТТЛ, 1948.

21. А.И. Вейник. Литье намораживанием. Минск, изд-во «Высшая школа», 1964.

22. А.И. Вейник. Тепловые основы теории литья. М., Машгиз, 1953.

23. А.И. Вейник. Испытания кокильных красок на теплопроводность. М., Машгиз, 1956.

24. А.И. Вейник. Теория особых видов литья. М., Машгиз, 1958.

25. А.И. Вейник. Приближенный расчет процессов теплопроводности. М.-Л., Госэнергоиздат, 1959.

26. А.И. Вейник. Теплообмен между слитком и изложницей. М., Металлургиздат, 1959.

27. А.И. Вейник. Теория затвердевания отливки. М., Машгиз, 1960.

28. А.И. Вейник. Литье в металлические формы. Минск, изд-во «Высшая школа», 1964.

ВЕЙНИК АЛЬБЕРТ ИОЗЕФОВИЧ

НОВАЯ СИСТЕМА ТЕРМОДИНАМИКИ ОБРАТИМЫХ И НЕОБРАТИМЫХ ПРОЦЕССОВ.

Минск, «Высшая школа», 1966,

48 стр. с илл.

Отредактировано Т. МАЙБОРОДА

на общественных началах

Техн. редактор Г. РОМАИЧУК

Худож. редактор Г. МАЛЫШЕВ

Корректор А. БЕЛЯНКИНА

AT 08143. Сдано в набор 18/IV 1966 г.

Подписано в печать 6/V 1966 г.

Формат 84X108 1/32. Бум. тип. № 7. Печ. л. 1,5.

Усл. печ. л. 2,58. Уч.-изд. л. 2,28.

Изд. № 66-76. Тип. зак. 417. Тираж 1000 экз.

Цена 14 коп.

Издательство «Высшая школа» Комитета по печати при Совете Министров БССР. Редакция физико-математической литературы. Тем. план 1966 г. (дополн.)

Минск, ул. Кирова, 24.

Типография издательства «Наука и техника» АН БССР и Комитета по печати при Совете Министров БССР.

Минск, Ленинский пр., 68.

⇐ Предыдущая 1 2 3 4 5 6 7 8 910