Закон состояния.

⇐ ПредыдущаяСтр 3 из 10Следующая ⇒

2. Закон состояния.

Потенциалы Р в числе прочих величин являются функциями состояния. Поэтому для них можно написать:

Р_i = f_i(Е₁; Е₂; ... ; Е_n) дж (14)

или (при n = 2)

Р₁ = f₁(Е₁; Е₂) дж. (15)

Р₂ = f₂(Е₁; Е₂) дж. (15)

Дифференцирование этих выражений дает

dP_i = 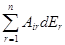(16)

где i = 1, 2, ..., n;

A_ii = (¶P_i/¶E_i)_Eин ; A_ir = (¶P_i/¶E_r)_Eин; ... ; A_ri = (¶P_r/¶E_i)_Eин (17)

и (при n = 2)

dР₁ = А₁₁dЕ₁ + А₁₂dЕ₂; (18)

dР₂ = А₂₁dЕ₁ + А₂₂dЕ₂; (18)

где

A₁₁ = (¶P₁/¶E₁)_E2 ; A₂₂ = (¶P₂/¶E₂)_E1; (19)

A₁₂ = (¶P₁/¶E₂)_E1 ; A₂₁ = (¶P₂/¶E₁)_E2 . (20)

Дифференциальные уравнения состояния (16) и (18) выражают закон состояния. В них основные коэффициенты А_ii , А₁₁ и A₂₂характеризуют количественную сторону влияния данного заряда на сопряженный с ним потенциал. Эти коэффициенты обратны емкостям К системы по отношению к соответствующим зарядам, т.е.

А_ii =1/К_ii ; А₁₁ = 1/К₁₁ ; A₂₂ = 1/К₂₂ . (21)

Перекрестные коэффициенты А_ir , А_ri, А₁₂ и А₂₁определяют количественную сторону влияния данного заряда на не сопряженные с ним потенциалы.

Примером может служить газ, в котором в числе прочих связаны между собой термическая и механическая внутренние степени свободы. Для газа

dT =A₁₁dS + A₁₂dV °K ; (22)

dp = A₂₁dS + A₂₂dV н/м², (22)

где

A₁₁ = (¶T/¶S)_V ; A₂₂ = (¶p/¶V)_S; (23)

A₁₂ = (¶T/¶V)_S ; A₂₁ = (¶p/¶S)_V. (24)

Изменение энтропии сопровождается одновременными изменениями как температуры, так и давления; аналогичная картина наблюдается при изменении объема. Величина А₁₁ обратна энтропиеемкости (термоемкости) К₁₁ , причем энтропиеемкость и теплоемкость связаны соотношением

С₁₁ = ТК₁₁ дж/град (25)

Если А_ir= А_ri = 0 и А₁₂ = А₂₁ = 0, то внутренние степени свободы оказываются не связанными между собой (взаимного влияния соответствующих явлений не происходит). При этом дифференциальные уравнения состояния (16) и (18) распадаются на независимые простейшие уравнения вида

dP_i = A_idE_i = dE_i/K_i (26)

В общем случае число связанных внутренних степеней свободы системы равно l £ n.

Дифференциальные уравнения состояния применимы для изучения любых явлений, они отражают связи между всеми переменными, существенными для системы, не делая исключения для энтропии, которая обычно изгоняется из уравнений состояния.

Для идеальных твердых, жидких и газообразных тел коэффициенты Аявляются константами. Интегрирование уравнений (16), (18) и (22) дает (принимается, что нулевым значениям зарядов отвечают нулевые значения потенциалов)

P_i = 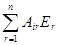(27)

где i = 1, 2, ..., n;

Р₁ = А₁₁Е₁ + А₁₂Е₂; (28)

Р₂ = А₂₁Е₁ + А₂₂Е₂; (28)

T =A₁₁S + A₁₂V °K ; (29)

p = A₂₁S + A₂₂V н/м², (29)

Калорическое уравнение состояния идеального тела при n =1 имеет вид

U = (1/2)KP² = (1/2)PE = (1/2)AE² дж (30)

Уравнения типа (27), (28) и (30) справедливы для всех явлений, включая термические, хотя для последних внутреннюю энергию принято сопоставлять не с квадратом температуры [формула (30)], а с температурой в первой степени. Общепринятая точка зрения базируется на случайных причинах (на свойствах обычного идеального газа Клапейрона). Поэтому в принципиальном отношении более правильными следует считать закономерности (26) н (30) Ими можно пользоваться наравне с общепринятыми (теплоемкость с температурой, как правило, растет, а энтропиеемкость - убывает) [10, 13]. Уравнение состояния (29) особого идеального газа автора отличается от уравнения Клапейрона прежде всего этим его свойством (у особого идеального газа внутренняя энергия сопоставляется с квадратом температуры).

Выражения (27) - (29) в новом аспекте представляют проблему абсолютного нуля температуры и других потенциалов. Для системы с несвязанными степенями свободы потенциал стремится к нулю при стремлении к нулю соответствующего заряда. Для системы со связанными степенями свободы данный потенциал стремится к нулю при стремлении к нулю всех зарядов (либо в нуль должны обращаться все коэффициенты А).

⇐ Предыдущая 1 234 5 6 7 8 9 10 Следующая ⇒