- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Статика.. Кинетика.
7. Статика.
В статике изучаются свойства стационарных равновесных однородных систем. В таких системах заряд находится в состоянии покоя, его величина со временем не изменяется. О покое заряда можно судить по отсутствию разности (перепада) DР потенциала внутри системы. С помощью критерия неравновесности условие покоя заряда определяется следующим образом:
KDP = DP/P << 1. (77)
Заметим, что критерий KDP неравновесности состояния похож на критерий Кд необратимости процесса.
Согласно неравенству (77) любой потенциал имеет во всем объеме системы одно постоянное значение. Это крайне облегчает аналитическое выражение состояния: для системы в целом, независимо от ее размеров, оказываются справедливыми все рассмотренные ранее дифференциальные уравнения термодинамики (в расчетах обычно принимается, что система имеет массу, равную 1 кг,или объем, равный 1 м3).
Количество тепла диссипации, выделяющегося в стационарной равновесной системе, равно нулю [формула (71)], так как DP = 0 [формула (77)]. Все процессы, протекающие в системе, обратимы.
Соответствующие системы рассматриваются в классической термодинамике (например, в разделе, посвященном использованию уравнений состояния, в том числе уравнения Клапейрона pv = RT, где R -газовая постоянная), в химии (где очень детально разработан раздел, связанный с изучением подвижного равновесия химических реакций) и т.д.
Общие дифференциальные уравнения состояния (16) справедливы для любых явлений. В частности, в работе [13] с их помощью анализируются термоэлектроупругость, термополяризация, термомагнетизм и т.д. Например, для термоупругих явлений имеем
dT =A11dS + A12dl °K ; (78)
dp = A21dS + A22dl н/м2, (78)
где S - удельная (объемная) энтропия, дж/(град*м3); dl - относительное удлинение стержня;
А12 = -А21 » -(Еa/С11)Т град; (79)
А11 = 1/К11 = Т/С11 м3град2/дж ; А22 = Е н/м2. (80)
Здесь Е - модуль упругости (Юнга) и a - коэффициент линейного расширения тела. Нижнее уравнение (78) соответствует закону упругости с учетом теплообмена.
Общее уравнение (27) может быть использовано для изучения пьезо- и пироэлектрических эффектов, электрострикции, поляризации и т.д.
Чрезвычайно плодотворно применение дифференциальных уравнений состояния для изучения химических и фазовых превращений. В работах [10, 13] показано, что при этом уравнения должны охватывать химическую (или фазовую), термическую, механическую, диффузионную и электрическую степени свободы (в работах [2, 3, 6, 8, 9] не учитываются все степени свободы, кроме химической, поэтому термодинамический метод оказывается бессильным).
8. Кинетика.
В кинетике рассматриваются свойства стационарных неравновесных систем, они не удовлетворяют условию (77). Такие системы заряд при своем движении пронизывает насквозь; количество заряда, содержащегося в системе, от времени не зависит.
Свойства систем изучаются с помощью пяти основных законов термодинамики, причем к процессам переноса непосредственно прилагаются дифференциальные уравнения (37), (39) и (40) - (43). Эти уравнения совместно с соотношениями взаимности (66) - (68) и равенством типа (75) составляют аппарат термодинамики необратимых процессов Онзагера [1-6, 8, 9]. Отсюда ясно, что термодинамика Онзагера является частным случаем общей теории автора.
Общая теория позволяет найти много важных закономерностей. Например, из общих соотношений (38) получаются следующие интересные равенства [10, 12, 13]:
В11/В22 = a11/a22 = b11/b22 = L11/L22 = M11/M22 = s = А22Р/А11Р = К11Р/К22Р ; (81)
В12/В11 = a12/a11 = b12/b11 = L12/L11 = M12/M11 = s12 = А11Р/А12Р = К12Р/К11Р ; (81)
Это - закон отношения проводимостей (отношение проводимостей для любой пары связанных внутренних степеней свободы равно отношению соответствующих емкостей).
Закон (81) позволяет осуществить многочисленные методы экспериментального определения физических свойств (теплоемкость, теплопроводность, электроемкость, электропроводность, диэлектрическая постоянная, магнитная проницаемость, вязкость, изотермическая сжимаемость и т.д.) различных твердых, жидких и газообразных тел. Например, для термоэлектрических явлений из выражений (81) получаем
LS/Ly = LQ/LyT = s = KS/Ky = KST/tY = C/tY в2/град2 (82)
где величины, относящиеся к энтропии, теплоте и электричеству, обозначены индексами S, Q и Y соответственно. Левая часть равенства (82) есть закон Видемана - Франца и Лоренца для металлов (согласно этому закону, s = 2•10-5 в2/град2[14]). Правая часть этого равенства показывает, что коэффициент о в действительности не постоянен, а равен отношению теплоемкости С к электроемкости tY (для металлов tY = 1012 град•ф/кг-атом),причем теплоемкость с уменьшением Т до нуля стремится к нулю.
На рис.1 кривая найдена с помощью правой части равенства (82), а точки - с помощью левой. Значения теплоемкости по Шредингеру и некоторые другие данные заимствованы из работы [14], величина Q есть характеристическая температура в теории теплоемкости Дебая. Кривая на рис.1 и равенство (82) могут быть использованы для определения одних величин (например, термических) по другим (электрическим).
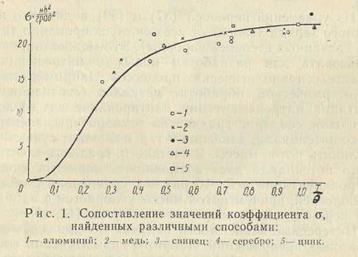
Равенство (82) справедливо также для неметаллических материалов. Например, для диэлектриков электроемкость пропорциональна диэлектрической постоянной. Одинаковость коэффициента и соблюдается в рамках определенных классов диэлектриков.
У жидкостей и газов термическая и электрическая степени свободы связаны с гидродинамической (и фильтрационной). Поэтому общее равенство (81) объединяет электрические и термические свойства материалов с гидродинамическими - вязкостью [обратна соответствующей проводимости - формула (46)], изотермической сжимаемостью (емкость по отношению к объему) и т.д. [13].
Из уравнений переноса (37) н (39) видно, что поток данного заряда зависит от всех сил одновременно (из числа связанных степеней свободы). Это можно широко использовать для разработки новых и интенсификации известных технологических процессов. Например, при химикотермической обработке металлов (азотизация, цементация, нитроцементация, алитирование и т.д.) дополнительное создание градиентов температуры, электрического потенциала, давления и т.д. позволяет существенно увеличить поток массы. В частности, градиент электрического потенциала дает возможность повысить скорость нитроцементации в 5-10 раз по сравнению с обычной технологией, причем поток массы ускоряется в направлении перемещения электрического заряда [13, 15].
Интересные зависимости получаются для химических и фазовых превращений. Например, при изучении процессов затвердевания и плавления, конденсации и испарения составляется совокупность из пяти уравнений (по числу степеней свободы). Если пренебречь электрической степенью свободы, то уравнения переноса принимают вид (индексом «д» отмечена диффузионная степень свободы):
Jm = - amdm - a12dT - a13dp - a14dmд кг/(м2сек) (83)
JS = - a21dm - aSdT - a23dp - a24dmд вт/(м2град) (83)
JV = - a31dm - a32dT - aVdp - a34dmд м/сек (83)
Jmд = - a41dm - a42dT - a43dp - amдdmд кг/(м2сек) (83)
где
a12 = a21 ; a13 = a31 ; a14 = a41 ; (84)
a23 = a32 ; a24 = a42 ; a34 = a43 . (84)
Умножив вторую строчку на температуру Т фазового превращения, найдем поток теплоты. Отношение
r = JQ/Jm = T(a21dm + aSdT + a23dp + a24dmд)/(amdm + a12dT + a13dp + a14dmд), дж/кг (85)
представляет собой удельную теплоту фазового превращения. При условиях, близких к равновесным (dT = 0, dр = 0, dmд = 0),
r = JQ/Jm = T(a21/am) = T(K21P/KmP) = C21P/KmP) дж/кг (86)
Для процессов испарения это теоретическое соотношение выражает известное опытное правило (закон) Трутона (отношение r/T есть величина, постоянная для всех веществ [14]).
Анализ общих законов позволил разработать теорию термодинамической пары [10-13, 15-18]. В паре наблюдается большое число различных эффектов. Она исключительно широко распространена в природе и технике.
Термодинамическая пара представляет собой два родственных (обладающих одинаковыми внутренними степенями свободы) проводника а и b, соединенных на концах (рис.2). Если между концами (спаями) пары создать разность некоторого потенциала DР1 , то в образованной таким образом замкнутой цепи возникает циркуляция второго н других (из числа связанных степеней свободы) зарядов (эффект циркуляции заряда).
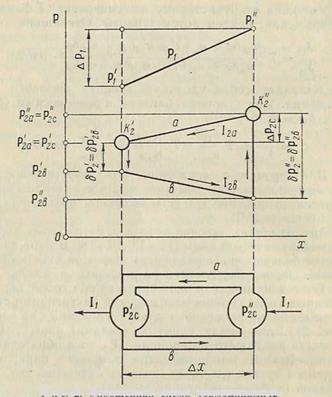
Рис.2. Упрощенная схема
термодинамической пары.
В спаях между проводниками аи bобразуются скачки второго потенциала dР2' и dР2" (эффект контактной разности потенциалов). При этом в одном спае происходит поглощение теплоты, а в другом - выделение (эффект контактной теплоты).
Перемещение порции второго заряда вдоль проводников (между спаями с разностью потенциалов DР1) сопровождается заряжанием и разряжанием ее первым зарядом (линейный эффект).
Если спаи обладают емкостями потенциала К2' и К2"по отношению ко второму заряду, то между этими емкостями об разуется разность DР2С второго потенциала (так называемая фиктивная движущая сила пронесен циркуляции второго заряда).
Полная движущая сила dР2 циркуляции второго заряда определяется формулой [13]
dР2/DР1 = (dР2к + dР2л)/ DР1 = (DП/DР1) + (sb - sa)I2 (87)
где П - скачок потенциала в любом из спаев; sa и sb – коэффициенты пропорциональности в выражении для линейной составляющей движущей силы (в проводниках а и b они различны);
I2 - сила тока (поток) циркулирующего заряда.
Контактная и линейная составляющие движущей силы обозначены буквами кил. Их величина определяется формулами
dР2к/DР1 = DП/DР1 = П/Р1 (88)
dР2л/DР1 = (sb - sa)I2 (89)
Простейшим случаем термодинамической пары является термоэлектрическая пара (термопара) Зеебека. Для нее полная и контактная электродвижущие силы (э.д.с.)
dj/DТ = DП/DТ + (sb - sa)I в/град; (90)
djк/DТ = DП/DТ = П/Т в/град. (88)
Отсюда видно, что полная э.д.с. термопары зависит от силы тока. Теории термоэлектричества, разработанная Томсоном, неверна, так как в первом соотношении Том-сона отсутствует множитель I [формула (90)], а во втором вместо контактной э.д.с. у Томсона фигурирует полная э.д.с. [формула (91)]. С этим обстоятельством необходимо считаться при использовании термопар для измерений температуры, а также при осуществлении с помощью термоэлементов различных охлаждающих и прочих (в частности, энергетических) устройств [19].
Например, по данным работы [20] при Т = 273°К и DТ= 100 градлинейная э.д.с. djл в термопаре платина - медь должна быть равна 1052 мкв, а непосредственные измерения, выполненные автором, дают величину, меньшую ±20 мкв (с такой максимальной возможной погрешностью измерялась линейная э.д.с). Эти данные подтверждают ошибочность теории Томсона и правильность теории автора (в обычных условиях работы термопары I сравнительно невелико, и поэтому фактическая величина djл , незначительна [13]).
Гальванический элемент и электрический аккумулятор также представляют собой типичную термодинамическую пару [13].
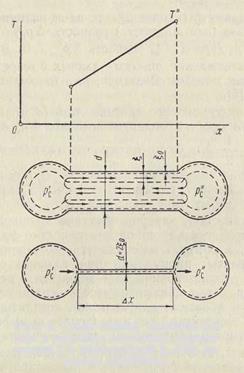
Другим характерным примером термодинамической пары является капилляр, в котором пристеночный слой вещества играет роль проводника b,а осевой - а.Если на концах капилляра создать некоторую разность потенциалов DР1 , то возникает циркуляция (фильтрация) этого вещества по схеме, изображенной на рис.3. При этом наблюдаются все упомянутые выше эффекты и, кроме того, происходит разделение сложного циркулирующего вещества на простые компоненты, которые скапливаются у концов капилляра (эффект разделения).
Термоосмос, фонтанный эффект в гелии II, кнудсеновское течение, капиллярность и т.д. - все эти явления, представляют собой частные случаи фильтрационной пары. Например, для термоосмоса, фонтанного эффекта, кнудсеновского течения и т.д. выражение (88) принимает вид (рис.3)
dрк/DТ = (dр" - dр')/DТ = dр'/Т' = dр"/DТ" н/(м2град) (92)
|
|
Рис.3. Упрощенная схема
фильтрационной пары (капилляр).
Если диаметр d капилляра равен двум толщинам x0 ,молекулярного (капиллярного) слоя (рис.4), то обратный ток газа или жидкости отсутствует (гидродинамическое сопротивление осевого слоя равно бесконечности). При этом фильтрационнодвижущая сила dр = dрк = dрС¥ (где dрС¥ -фиктивная движущая сила при 
 t = ¥), а скачки давления для обычного идеального газа dр' = (1/2) dрс' и dр" = (1/2) dрс". В результате формула (92) совпадает с известным выражением, полученным методом Онзагера [2, 3].
t = ¥), а скачки давления для обычного идеального газа dр' = (1/2) dрс' и dр" = (1/2) dрс". В результате формула (92) совпадает с известным выражением, полученным методом Онзагера [2, 3].
Если диаметр больше 2x0 , то из-за наличия обратного тока газа (или жидкости) разность dрС¥ становится меньше dрк (при d >> x0 разность dрС¥ = 0). Этим объясняется несовпадение опытных данных с теоретическими, найденными методом Онзагера, на что имеется ссылка в работе [5].
Для кнудсеновского течения газа (dменьше длины свободного пробега молекул) величина dрк приближенно равна (1/2) dрС¥ (если считать, что газ несжимаем) [13].
Изучение явления капиллярности с позиций общей теории показывает, что известная формула Лапласа, определяющая избыточное давление dрС¥ под искривленной поверхностью, неверна. Фактически жидкость в капилляре представляет собой поверхностно-фильтрационную пару, в которой наблюдаются все перечисленные выше эффекты: циркуляции (при наличии смачивания жидкость в пристеночном слое движется к мениску, там испаряется, затем конденсируется в осевом слое и в нем движется в обратном направлении), контактной разности давлений, контактной теплоты (тепловой эффект процессов испарения и конденсации), возникновения dрС¥ , разделения и т.д. Согласно формуле (92), максимальная разность давлений dрС¥ = dрк в капилляре получается при d = 2x0 , она имеет конечное значение (согласно формуле Лапласа, при d ® 0 разность dрС¥ ® ¥).
|
|
Рис.4. Схема течения жидкости или
газа в закрытых капиллярах (пристеночный x
и молекулярный x0 слои показаны пунктиром).
Новая теория хорошо объясняет зависимость DрС¥ от влажности и давления окружающей среды (которые влияют на интенсивность отсоса циркулирующего пара от мениска). Из нее также следует, что известная формула Стефана для определения интенсивности испарения жидкости из капилляра не отражает физического существа процесса.
Количественный теоретический [с привлечением уравнений (40) - (43), учитывающих сопротивления проводников а и bпары] и эскпериментальный анализ различных термодинамических пар показывает, что в них разность DрС изменяется со временем по экспоненциальному закону, величина DрС¥ не зависит от длины Dх капилляра, но резко возрастает с уменьшением его диаметра d, скорость wb движения жидкости и газа в пристеночном слое пропорциональна градиенту потенциала DР1/Dх и обратно пропорциональна температуре и т.д.
Согласно общей теории, каждая степень свободы создает по отношению к другим (связанным) все те эффекты, которые присущи термодинамическим парам. Автором установлено, что в газах связаны между собой термическая, механическая, химическая, диффузионная, фильтрационная, электрическая, магнитная, вибрационная (волновая) и другие степени свободы (почти те же связи имеются в твердых и жидких телах). Отсюда следует, что общее число возникающих эффектов чрезвычайно велико. Например, под действием разности температур DТ в капилляре возникают разности DрС¥ давлений, электрических (соответствующий эффект экспериментально обнаружен 3.Ф. Слезенко [13]) и химических потенциалов и т.д. Автор наблюдал скольжение газа под действием разности электрических потенциалов и скольжение жидкости под действием разности химических потенциалов и т.п. Однако большинство из имеющихся эффектов еще никто не наблюдал и не пытался использовать.
Эффекты циркуляции и разделения очень широко распространены в природе (обмен в капиллярах и полупроницаемых перегородках живых организмов, циркуляция влаги и газа в почвах и грунтах, и т.д.) и находят все большее применение на практике. Приведем несколько примеров.
Эффект разделения используется в хроматографии для определения состава жидкостей и газов, а также в технике для разделения газов и изотопов.
Процессы переноса энтропии, влаги (с учетом испарения и конденсации) и газа в капиллярнопористом теле подчиняются рассмотренным выше законам. В частности, под действием возникающих разностей температур и химических потенциалов в капиллярах и порах песчано-глинистой литейной формы (в период ее сушки, а так же после заливки металла) происходит интенсивная циркуляция воды (в виде пара и жидкости) по схеме, изображенной на рис.3. Термодинамический механизм циркуляции таков, что жидкость и пар (речь идет о водяном паре, находящемся в сухом теле в смеси с воздухом) подсасываются к горячей зоне (горячему спаю пары). Во влажном теле вследствие действия разности парциальных давлений пар переносится в холодную зону и там конденсируется. При большой интенсивности процесса возникающая разность давлений выжимает жидкость к холодной зоне.
Детальный термодинамический анализ процесса конвективной сушки литейных форм и стержней (с учетом возникающих давлений и напряжений) позволил разработать высокотемпературный режим сушки, ускоряющий процесс в 2-3 раза [16]. На этой же основе был создан весьма эффективный метод сушки форм и стержней в электрическом поле высокой частоты. Он в 10-60 раз ускоряет сушку (по сравнению с конвективной), повышает качество изделий, улучшает условия труда и более выгоден в экономическом отношении [16]. Производственное опробование метода показывает, что высокочастотное сушильное устройство окупается в течение 6 месяцев.
Интересен механизм высокочастотной сушки. Испарение жидкости происходит в интервале (спектре) температур. Величина интервала и его температурный уровень, а также величина спектральной теплоты парообразования зависят от состава жидкости, количества и состава растворенных примесей, форм связи жидкости и материала тела и т.д. Путем введения в крепитель специальных добавок (например, диэтиленгликоля, глицерина, формамида и т.д.) удается на десятки и сотни градусов повысить температуру испарения и тем самым добиться нужного режима отвердевания крепителя.
Затвердевание металла в интервале температур DТкр сопровождается образованием сетки кристаллов и фильтрацией в межкристаллических капиллярах жидкой фазы под действием градиентов температуры, химического и поверхностного (явления капиллярности) потенциалов. Эффект разделения приводит к выносу легких компонентов сплава (с малой атомной массой) к центру отливки, а тяжелых - на периферию (так называемая ликвация [15, 16]).
Перед фронтом затвердевающего металла движется фронт вынесенных ликватов (примесей). Этот эффект (разделения) используется для очистки металлов методом зонной плавки [19]. При наличии межкристаллических капилляров преобладающим механизмом в процессе зонной плавки является термофильтрация, а при отсутствии - термодиффузия.
Эффект фильтрации жидкой фазы используется для получения особо плотных отливок без усадочных раковин и пористости [16, 17]. На этой основе автором разработаны новые методы отливки чугунных труб намораживанием (путем вытягивания твердой корки, образующейся на внутренней поверхности стакана с металлом) и прокатки жидкого металла [16, 21].
Создан также весьма эффективный метод поверхностного легирования отливок. Легированный слой образуется вследствие круговой циркуляции (фильтрации) жидкой фазы в межкристаллических (межзерновых) капиллярах отливки и обмазки, покрывающей внутреннюю поверхность формы. Циркуляция происходит под действием градиентов температуры и химического потенциала (концентрации). Решающим фактором в процессе циркуляции является эффект смачивания обмазки металлом отливки.
Например, были испытаны чугунные отливки, легированные различными ферросплавами. Из каждого ферросплава определенного фракционного (0,25-0,5 мм)и химического состава готовились три обмазки - смачиваемая, плохо смачиваемая и несмачиваемая. Для получения смачиваемой обмазки порошок ферросплава смешивается в пропорции 3:1с флюсом (бура, борная кислота и хлористый натрий в пропорции 1:1:1), плохо смачиваемая обмазка получается по общепринятой технологии (порошок замешивается на патоке или жидком стекле), несмачиваемая обмазка готовится путем окисления поверхности зерен в «кипящем слое» (в потоке кислорода) и замасливания крепителем П. Все обмазки (были испытаны Fe-V, Fe-W, Fe-Cr, Fe-Mn, Fe-Mo, Fe-Si, Mn, Cr и Si) разводятся водой до пастообразного состояния и в таком виде наносятся на форму.
С обмазками первого типа получен хороший легированный слой (кроме Si), независимо от температуры плавления обмазки и других факторов; с обмазками второго типа слой получен только для двух случаев (с Fe-Мп и Fe-Si); обмазки третьего типа легированного слоя не дают.
Толщина легированного слоя может изменяться от долей миллиметра до десятков миллиметров, в него может быть введен практически любой элемент таблицы Менделеева.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|