Закон переноса.

3. Закон переноса.

Обобщенные дифференциальные уравнения переноса зарядов легко получить, если выразить с помощью уравнений (15) заряды через потенциалы, т.е.

E₁ = f₁(P₁; P₂); (31)

E₂ = f₂(P₁; P₂). (31)

Дифференцирование этих уравнений дает

dE₁ = K_11PdP₁ + K_12PdP₂ ; (32)

dE₂ = K_21PdP₁ + K_22PdP₂ ; (32)

где

К_11Р = (¶Е₁/¶Р₁)_Р2 ; К_22Р = (¶Е₂/¶Р₂)_Р1; (33)

К_12Р = (¶Е₁/¶Р₂)_Р1 ; К_21Р = (¶Е₂/¶Р₁)_Р2; (34)

В уравнениях (32) количества переданных зарядов непосредственно сопоставляются с разностями потенциалов, причем роль обобщенных проводимостей играют емкости К_Р при постоянных значениях потенциалов.

Чтобы придать дифференциальным уравнениям переноса более привычный и удобный для расчетов вид, введем понятия потока заряда W, кинетической силы V и закона переноса. Имеем

W = DdE ; V = -CdP ; W = DV . (35)

Коэффициенты пропорциональности В, С и D объединяются соотношениями:

А_Р = -D/ВС ; К_Р = - ВС/D . (36)

Для двух внутренних степеней свободы (n = 2) из выражений (32) и (35) получаем

W₁ = B₁₁V₁ + B₁₂V₂ ; (37)

W₂ = B₂₁V₁ + B₂₂V₂ ; (37)

где

B₁₁ = -(D/C)K_11P ; B₂₂ = -(D/C)K_22P ; (38) B₁₂ = -(D/C)K_12P ; B₂₁ = -(D/C)K_21P ; (38)

В общем случае для nвнутренних степеней свободы дифференциальные уравнения переноса имеют вид

W_i = 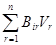(39)

где i = 1, 2, ..., n.

Основные коэффициенты B_ii , B₁₁ и В₂₂ в уравнениях (37) и (39), выражающих закон переноса, представляют собой проводимости системы по отношению к соответствующим зарядам; перекрестные коэффициенты (увлечения) B_ir, B_ri , В₁₂ и В₂₁ характеризуют взаимное влияние потоков. Если B_ir = B_ri = 0 и В₁₂ = В₂₁ = 0, то взаимного влияния потоков нет, совокупности уравнений (37) и (39) распадаются на независимые простейшие уравнения типа законов Фурье, Ома, Фика и т.д.

Всего можно предложить восемь конкретных вариантов выбора потоков и сил (коэффициентов В, С и D) [13]. Наиболее употребительные из них имеют вид [10, 13]:

J = dE/Fdt ; X = -dP ; J = aX ; (40)

I = dE/dt ; X = -dP ; I = bX ; (41)

J = dE/Fdt ; Y = -dP/dx ; J = LY ; (42)

I = dE/dt ; Y = -dP/dx ; I = MY , (43)

где J и I – потоки;

X и Y – силы (dР - напор потенциала на поверхности системы, dP/dx – градиент потенциала в сечении системы);

a и b - коэффициенты отдачи заряда на поверхности;

L и М – проводимости;

F – площадь, м²;

t – время, сек.

Переход от силы X к Y и наоборот [согласно теореме Кюри в уравнениях (37) и (39) нельзя одновременно сочетать скаляры и векторы] осуществляется с помощью подстановок [10, 13]

a = L/Dх ; b= М/Dх , (44)

где Dx - некоторый размер, м.

Заметим, что для термических явлений коэффициенты энтропиепроводности B_S (в законе переноса энтропии) и теплопроводности B_Q (в законе теплопроводности Фурье) связаны соотношением

B_Q = TB_S . (45)

Оба типа коэффициентов могут использоваться на равных правах.

Для гидродинамических явлений проводимость L_V (по отношению к объему) выражается через динамическую вязкость h и диаметр dтрубопровода следующим образом:

L_V = (1/h)(d²/32) м⁴/(н*сек) . (46)

Эта формула справедлива для ламинарного потока (найдена с помощью законов Дарси и Гагена – Пуазейля [10, 13]).

⇐ Предыдущая 1 2 345 6 7 8 9 10 Следующая ⇒