
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Основные формулы. Примеры решения задач
Основные формулы
Электроёмкость конденсатора
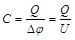 ,
,
где Q – заряд конденсатора (т.е. заряд одной из его пластин); Δφ – разность потенциалов ; U – напряжение на конденсаторе.
Электроёмкость плоского конденсатора
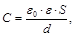
где ε0 = 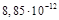 Ф/м – электрическая постоянная; ε – диэлектрическая проницаемость диэлектрика, заполняющего конденсатор; S – площадь одной пластины конденсатора; d – расстояние между пластинами.
Ф/м – электрическая постоянная; ε – диэлектрическая проницаемость диэлектрика, заполняющего конденсатор; S – площадь одной пластины конденсатора; d – расстояние между пластинами.
Электроёмкость сферического конденсатора
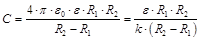 ,
,
где R1, R2 – радиусы внутренней и внешней концентрических сфер; 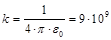 м/Ф.
м/Ф.
Электроёмкость цилиндрического конденсатора
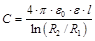 ,
,
где l – длина соосных цилиндров; R1, R2 – радиусы внутреннего и внешнего цилиндров.
Электроёмкость «С» последовательно соединённых конденсатором определяется из равенства
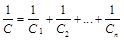 .
.
Общее напряжение U и заряд Q системы последовательно соединённых конденсаторов в количестве «n»: 
U=U1+U2+…+Un;
Q=Q1=Q2=…=Qn.
Электроемкость «С», общее напряжение U и заряд Q системы «n» параллельно соединённых конденсаторов
С=С1+С2+…+Сn;
U=U1=U2= …=Un;
Q=Q1+Q2+…+Qn.
Энергия W конденсатора (энергия его электрического поля)
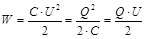 .
.
Объёмная плотность энергии электрического поля
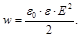
Примеры решения задач
Пример 1
Три конденсатора, имеющие электроёмкости С1 = 1 мкФ, C2 = 3 мкФ, С3 = 6 мкФ, соединены последовательно и подключены к источнику с напряжением U = 120 B. Найти напряжение на третьем конденсаторе.
Дано:
C1 = 1 мкФ = 10-6 Ф
С2 = 3 мкФ = 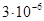 Ф
С3 = 6 мкФ = Ф
С3 = 6 мкФ = 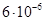 Ф
U = 120 В Ф
U = 120 В
|
| U3-? |
Решение
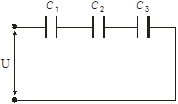
Общую электроёмкость определим из формулы
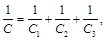
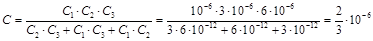 Ф.
Ф.
Общий заряд Q равен каждому из зарядов Q1, Q2 и Q3:
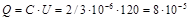 Кл.
Кл.
Тогда Q3 = 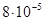 Кл.
Кл.
Напряжение на третьем конденсаторе U3 = 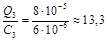 В.
В.
Ответ: U3 = 13,3 B.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|