
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Примеры решения задач
Примеры решения задач
Пример 1
Три точечных заряда Q1 = 1 мкКл, Q2 = -2 мкКл, Q3 = 4 мкКл находятся на бесконечно больших расстояниях друг от друга. Найти: а) работу, которую нужно совершить, чтобы расположить заряды в вершинах правильного треугольника со стороной а = 0,1 м;
б) потенциальную энергию заряда Q1 после перемешения зарядов.
Дано:
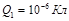
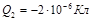
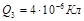
|
| а) А -? б) Wn1 -? |
Решение
После перемещения зарядов:
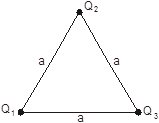
а) Работа А равна изменению потенциальной энергии: А = |Wnкон - Wnнач|.
Wnнач = 0; Wnкон = W12 + W23 + W13;
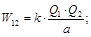
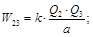
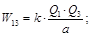
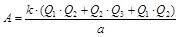 .
.
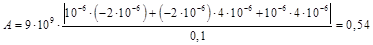 Дж.
Дж.
б) 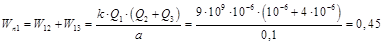 Дж.
Дж.
Ответ: а) А = 0,54 Дж; б) Wn1 =0,45 Дж.
Пример 2
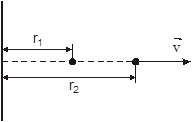
Бесконечная тонкая равномерно заряженная нить имеет линейную плотность заряда 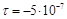 Кл/м. Какую скорость приобретет электрон, переместившись из точки на расстоянии r1 = 0,1 м в точку на расстоянии r2 = 0,2 м от нити? Отношение модуля заряда электрона к его массе
Кл/м. Какую скорость приобретет электрон, переместившись из точки на расстоянии r1 = 0,1 м в точку на расстоянии r2 = 0,2 м от нити? Отношение модуля заряда электрона к его массе 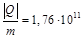 Кл/кг. Начальная скорость электрона равна нулю.
Кл/кг. Начальная скорость электрона равна нулю.
Дано:
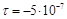 Кл/м
r1 = 0,1 м
r2 = 0,2 м Кл/м
r1 = 0,1 м
r2 = 0,2 м
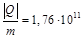 Кл/кг
υ0 = 0 Кл/кг
υ0 = 0
|
| υ = ? |
Решение
По теореме о кинетической энергии работа 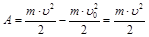 , т.к.
, т.к. 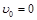 .
.
С другой стороны, работа А
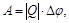 тогда
тогда 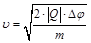 .
.
Из уравнения, связываюшего потенциал и напряженность электрического поля в случае цилиндрической симметрии 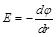 , следует:
, следует: 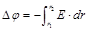 .
.
Напряженность Е поля нити 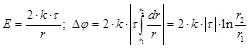 . Тогда скорость
. Тогда скорость 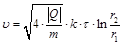 .
.
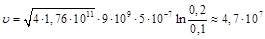 м/с.
м/с.
Ответ: 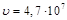 м/с.
м/с.
Пример 3
Диэлектрический шар радиусом 0,2 м с 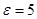 равномерно заряжен по объему с объемной плотностью заряда
равномерно заряжен по объему с объемной плотностью заряда 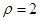 мкКл/м3. Найти разность потенциалов между точками, расположенными на расстояниях r1 = 0,1 м и r2 = 0,4 м от центра шара.
мкКл/м3. Найти разность потенциалов между точками, расположенными на расстояниях r1 = 0,1 м и r2 = 0,4 м от центра шара.
Дано:
R = 0,2 м
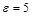
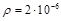 мкКл/м3
r1 = 0,1 м
r2 = 0,4 м мкКл/м3
r1 = 0,1 м
r2 = 0,4 м
|
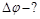
|
Решение
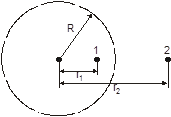
Связь Е и 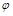 для центрально симметричного поля
для центрально симметричного поля
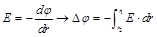 .
.
Напряженность электрического поля шара в зависимости от расстояния r до центра шара
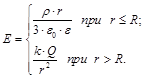
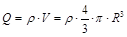 – электрический заряд шара.
– электрический заряд шара.
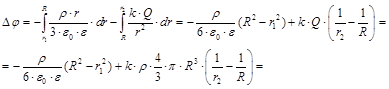
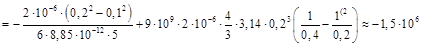 В.
В.
Ответ: 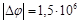 В.
В.
Пример 4
Две тонкие концентрические металлические сферы радиусами R1 = 0,2 м и R2 = 0,4 м имеют заряды Q1 = 200 нКл и Q2 = -160 нКл. Найти потенциалы электрического поля в точках А, В и С, расположенных на расстояниях rA = 0,1 м; rB = 0,3 м; и rC = 0,5 м от общего центра сфер.
Дано:
R1 = 0,2 м
R2 = 0,4 м
Q1 = 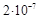 Кл
Q2 = Кл
Q2 = 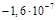 Кл
rA = 0,1 м
rB = 0,3 м
rC = 0,5 м Кл
rA = 0,1 м
rB = 0,3 м
rC = 0,5 м
|
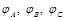 - ? - ?
|
Решение
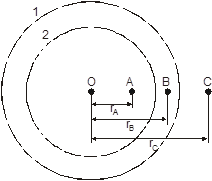
Потенциал внутри первой сферы 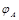 одинаков во всех точках внутри этой сферы и по принципу суперпозиции для потенциалов
одинаков во всех точках внутри этой сферы и по принципу суперпозиции для потенциалов
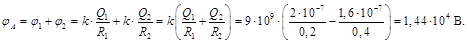 Потенциал
Потенциал 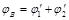 ,
,
где 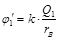 совпадает с потенциалом поля точечного заряда, равного Q1 и расположенного в т. О;
совпадает с потенциалом поля точечного заряда, равного Q1 и расположенного в т. О; 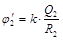 – потенциал поля, создаваемого сферой «2» во всех точках между сферами.
– потенциал поля, создаваемого сферой «2» во всех точках между сферами.
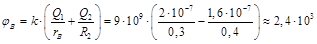 В.
В.
Потенциал 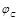 в точке вне обеих сфер совпадает с потенциалом поля точечных зарядов, равных Q1 и Q2 , помещенных в т. O:
в точке вне обеих сфер совпадает с потенциалом поля точечных зарядов, равных Q1 и Q2 , помещенных в т. O: 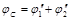 , где
, где 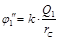 ,
, 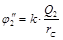 .
.
Тогда
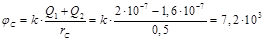 В.
В.
Ответ: 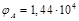 В,
В, 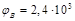 В,
В, 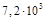 В.
В.
Пример 5
Тонкое кольцо радиуса R = 0,3 м равномерно заряжено с линейной плотностью заряда 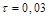 мкКл/м. Найти работу по перемещению точечного заряда Q = 20 нКл из центра кольца вдоль оси кольца на расстояние h = 0,4 м плоскости кольца.
мкКл/м. Найти работу по перемещению точечного заряда Q = 20 нКл из центра кольца вдоль оси кольца на расстояние h = 0,4 м плоскости кольца.
Дано:
R = 0,3 м
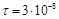 Кл/м
Q = Кл/м
Q = 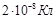 h = 0,4 м
h = 0,4 м
|
| A - ? |
Решение
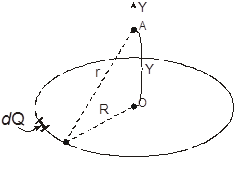
Выберем ось координат, совпадающую с осью кольца с началом в центре кольца. Определим зависимость потенциала кольца от расстояния «Y» до его центра. По принципу суперпозиции для потенциалов
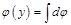 ,
,
где 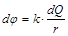 ;
; 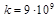 м/Ф;
м/Ф; 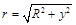 .
.
Для всех зарядов dQ кольца расстояние r до точки А, в которой вычисляем потенциал, есть величина постоянная, следовательно,
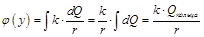 ,
, 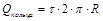 ,
, 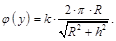
Работа А по перемещению заряда Q из центра кольца в точку, расположенную на оси кольца на расстоянии h от его плоскости,
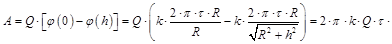
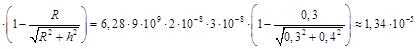 Дж.
Дж.
Ответ: 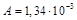 Дж.
Дж.
Пример 6
Два электрона, находясь первоначально на бесконечном расстоянии друг от друга, движутся навстречу друг другу со скоростями, равными по величине 10 м/с. На какое минимальное расстояние сблизятся электроны?
| Дано: υ0 = 10 Мм/с = 107 м/с |
| rm - ? |
Решение
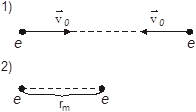
По закону сохранения энергии
W1 = W2 , или 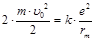 ,
,
где 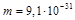 кг,
кг, 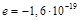 Кл – масса и заряд электрона.
Кл – масса и заряд электрона.
Отсюда 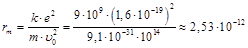 м.
м.
Ответ: rm = 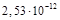 м.
м.
Пример 7
В условиях предыдущей задачи один из электронов первоначально покоился. Найти минимальное расстояние между электронами.
Дано:
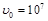 м/с м/с
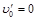
|
| rm -? |
Решение
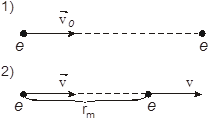
а) По закону сохранения импульса 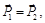 или
или 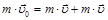 , где
, где 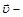 скорость каждого электрона в момент наибольшего сближения. Имеем
скорость каждого электрона в момент наибольшего сближения. Имеем 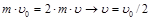 .
.
б) По закону сохранения энергии W1 = W2 , или 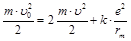 , или
, или 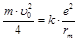 .
.
Отсюда 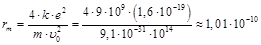 м.
м.
Ответ: 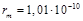 м.
м.
Замечание: равенство скоростей электронов в момент их наибольшего сближения, когда потенциальная энергия их взаимодействия максимальна, означает, что их кинетическая энергия минимальна, что достигается тогда, когда скорость относительного движения минимальна, т.е. равна нулю.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|