ПРЕДИСЛОВИЕ 4 страница

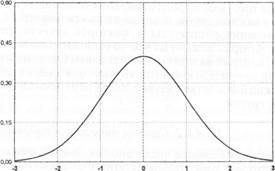
Рис. 1. График нормального закона распределения - по горизонтальной оси отложены стандартные отклонения, а по вертикальной - вероятность встречаемости такой выраженности качества в генеральной совокупности.

Сигма обладает одним замечательным свойством, делающим ее популярной в научных исследованиях: она позволяет сравнивать между собой показатели, полученные при измерении разных качеств. Например, бессмысленно проводить сравнение температуры тела в градусах с ростом в миллиметрах или оценивать, насколько далеко от среднего находится индивид по некоему качеству (например, интеллекта), измеренному в одних единицах и по одной шкале, в отличие от другого качества (например, тревожности), измеренному в других единицах и по другой шкале. Приведение показателей этих шкал к размерности сигмы такие количественные сравнения позволяет. Стандартная шкала, измеряющая что-либо в стандартных отклонениях (в сигмах) называется Z-шкалой.

Чем ближе показатель конкретного человека, представленный в шкальных баллах стандартного отклонения, лежит к 0 (в идеале - к той точке, на которой расположена средняя), тем выше вероятность встречаемости такой выраженности данного качества в выборке. И наоборот - чем больше он приближается к 3, и «+» и «-», тем эта вероятность меньше. Если несколько упростить о&ьяснения, то можно сказать, что в точке со значением -3 находится индивид с самой малой из известных выраженностью данного качества, а в точке +3 - с самой большой из известных.

После средней, стандартное отклонение - основное свойство экспериментальной и контрольной групп, которое должно быть количественно определено в разделе дипломной работы, описывающей ваши эмпирические материалы. Эти два базовых показателя являются основой для всех дальнейших расчетов, производимых с целью подтверждения выдвинутой в работе гипотезы.

❖ Расчет процентов

Это самый низкий и примитивный способ анализа, целесообразный в тех случаях, когда приходится сравнивать или отслеживать изменения среди носителей отличающихся качеств. Например, процент лиц с девиантным поведением (в отличие от нормативного) в группе может характеризоваться до эксперимента одним числом, а после - другим. В другом случае подобный анализ применим при показе, например, разницы в выявленных процентах наркоманов среди юношей и девушек (качественные различия по полу и по наличию зависимости), либо при характеристике удельного веса лиц, обладающих какой-то способностью (предположим, справляющихся с заданиями теста) в зависимости от возраста и т. п. Расчет процентов выглядит совершенно неубедительно, если численность обследуемой группы мала.

❖ Достоверностьразличий

Довольно частой задачей исследования является сравнение средних, то есть подтверждение существенных различий между средними, вычисленными для двух выборок (выборочных средних). Для этой цели принято использовать специальный критерий t Стъюдента, который позволяет выяснить - достоверны ли эти различия. Исследовательская практика выработала три основных порога вероятности безошибочных прогнозов подобного рода (0,999; 0,99 и 0,95 или вероятности ошибки прогноза 0,001, 0,01 и 0,05), которые соответствуют стандартным значениям t Стъюдента. Это уровень вашего доверия или недоверия к полученным материалам.

После расчета по специальной формуле эмпирического (в вашем исследовании) критерия разности, вы должны сравнить его со стандартными величинами, которые можно найти в соответствующих справочных таблицах. Если первый равен стандартному или превышает его, то тогда полученные различия средних считаются достоверными и могут соответствующим образом интерпретироваться. Если нет, то факт неподтвержденных различий либо игнорируется в дальнейшем тексте диплома, либо, при необходимости, подчеркивается. Легко запомнить, что, если вы получили эмпирический критерий достоверности более 2,00, то различия средних двух выборок уже статистически значимы.

В тексте диплома должен быть указан эмпирический критерий (t Д приведен табличный критерий (t _Ст) для суммы объемов сравниваемых выборок (п) и вероятность ошибки сделанного допущения о том, что средние отличаются. Например:

t _э - 2,78; п = 30; t _Ст= {2,05-2,76-3,67};р <= 0.01

Из приведенного примера видно, что для случайного получения такого эмпирического критерия (2,78) при сравнении двух групп, общей численностью 30 человек (например, 14 и 16) нужно провести, по крайней мере, сто сравнений (вероятность ошибки - одна сотая).

❖ Корреляционный анализ

Другой часто встречающийся вариант статистической обработки полученных материалов - установление степени связи между собой двух и более переменных. В принципе в науке рассматриваются два типа связей. Первые называются функциональными - при изменениях одного признака (независимого) на определенную величину всегда изменяется и второй признак (зависимый) тоже на строго определенную величину Например, радиус и длина окружности. Функциональные связи встречаются только в идеальных условиях, когда предполагается, что никаких посторонних влияний нет.

При изучении живых биологических объектов, физиологических характеристик и психических процессов приходится иметь дело со вторым типом связей, при котором определенному значению первого признака в группе соответствует не одно значение второго признака, а целое их распределение. Этому в немалой степени способствует многообразие воздействующих на второй признак факторов, которые учесть все просто невозможно. Такая связь называется корреляционной или просто корреляцией. Например, при одном и том же уровне общего внимания у учеников какого-то класса, эффективность решения ими арифметических задач будет различная.

В силу неполной зависимости одного признака от другого корреляционная связь не может быть точной. Результатом ее вычисления является т. н. коэффициент корреляции (Пирсона-г), числовой показатель которого может лежать в диапазоне от -1 до +1. Чем он ближе к нулю, тем слабее зарегистрированная связь, чем ближе к единице, тем она мощнее. Если полученный вами коэффициент корреляции положителен, то связь прямая - с ростом одного признака растет и другой. Если он отрицателен, то связь обратная - при увеличении первого признака второй уменьшается или увеличивается при уменьшении первого.

На показатель корреляционных отношений, как и на многие другие расчетные характеристики, распространяется требование учета его достоверности (р <=0.05;/? <= 0.01 \р <= 0.001), зависимой от численности коррелирующих выборок.

Форма представления коэффициента корреляции в дипломе такова:

г=-0,37;/? <=0.05

Если по ходу исследования выясняется, что коррелирующих между собой переменных много, то целесообразно представить всю их совокупность в виде корреляционного графа, в котором сами переменные обозначаются заключенными в кружки цифрами, а связи между ними - соединяющими линиями. Характер линий будет зависеть от знака связи. Например, для положительной корреляции линию прорисовывают сплошной, а для отрицательной - пунктирной, давая соответствующие пояснения в подрисуночной подписи или в тексте.

В некоторых экспериментах приходится встречаться со случаями, когда один или оба из интересующих показателя отличаются качественно или только наличием или отсутствием какой-то характеристики (например, признак «мальчик - девочка» сопоставляется с признаком «ловкий - неуклюжий»). Иначе такие ряды можно представить в виде нулей и единиц. При подобных обстоятельствах тоже есть возможность вычислить степень связи между одним из этих альтернативных признаков

№	Признак 1	Признак 2







п

и другой переменной, но уже с помощью иного расчетного показателя - тетрахорического коэффициента корреляции.

Привлекательность тетрахорического коэффициента корреляции связана с чрезвычайной простотой его расчета, который можно произвести за несколько минут.

В принципе, любой признак, даже имеющий в группе количественный разброс, можно задать нулями и единицами, разбив его на показатели больше и меньше средней и тогда коррелируемые ряды приобретают вид.

Обратите внимание на то, чтр даже статистически значимый коэффициент корреляции, в отличие от функциональных отношений, ничего не говорит о содержании связи между переменными. В принципе возможны три варианта интерпретации полученной корреляции:

- одна переменная действительно причинно зависима от другой;

- обе переменных закономерно меняются не из-за того, что одна обусловливает вторую, а из-за того, что они обе обусловливаются третьей, более общей переменной (одна неизвестная независимая, две известные и одинаково зависимые);

- обнаруженная связь случайна (при большом числе изучаемых переменных такое возможно примерно в каждом двадцатом случае) - артефакт.

В результате некоторых статистических расчетов вы можете столкнуться со случаями, когда коэффициент корреляции достаточно велик и обнаруженная связь хорошо описывается с точки зрения здравого смысла, но величина самого коэффициента не достигает приемлемого уровня значимости (вероятность ошибки р>0 05). При подобных обстоятельствах, чтобы не потерять ценной информации,вполне возможно говорить о тенденции корреляции.

❖ Регрессионный анализ

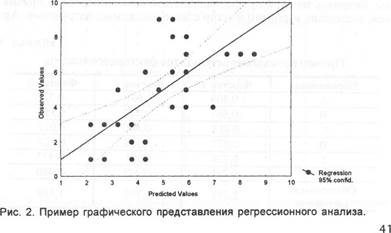
При необходимости получить информацию о том, на какую величину изменяется один признак при изменении значения другого на одну единицу измерения, используется коэффициент прямолинейной регрессии (R). С его помощью, например, можно решить вопрос, на сколько минут увеличивается продолжительность сна при увеличении дозы снотворного на 1 миллиграмм. Во всех случаях расчета этого коэффициента следует иметь в виду, что его корректные значения будут получены только если ожидаемая зависимость между измеряемыми переменными действительно прямолинейна или почти прямолинейна (рис. 2). Если она, например, n-образна, то расчеты дадут искаженные результаты.

❖ Дисперсионный анализ

Если одной из поставленных вами в дипломной работе задач является исследование силы влияния какого-то фактора или факторов на изучаемый признак, то адекватным математическим приемом учета этого влияния является дисперсионный анализ. Смысл дисперсионного анализа может быть сведен к следующим рассуждениям:

- количественный спектр какого-то признака, (например, вербального интеллекта), его рассеяние от средней в группе называется дисперсией (к слову сказать, близкая к дисперсии характеристика рассеяния - сигма, есть ни что иное, как корень квадратный из дисперсии);

- количественное разнообразие признака в группе объясняется воздействием множества факторов;

- влияние какого-то конкретного фактора будет приводить к изменениям дисперсии (в этом суть влияния) на вполне конкретную величину;

- влияние части факторов в исследовании может быть учтено (то есть они измеряются), а части - остается за пределами возможностей экспериментатора;

- сила влияния будет определяться как отношение частной дисперсии, вызванной воздействием данного фактора к общей дисперсии;

- сочетанное влияние двух или более факторов может приводить к эффектам, отличным от влияния каждого из них в отдельности;

- следовательно, общая дисперсия будет определяться несколькими переменными: частными, сочетанными и неучтенными влияниями, ошибками, допущенными во время измерения.

Дисперсионный анализ как раз и позволяет учесть роль каждой из этих составляющих, причем может это сделать как для одного влияющего фактора, так и для нескольких (правда, сложность расчетов в последнем случае резко возрастает).

❖ Факторный анализ

Если перед вами стоит задача компактного описания или построения схемы классификации большого информационного массива, то

лучшим математическим приемом для этого является факторный анализ. Созданный специально по заказу психологов, факторный анализ призван описывать небольшим числом функциональных единиц (факторов, основных, независимых показателей) многочисленные, разнородные, а порой мозаичные явления. Например, с помощью факторного анализа результатов исследования по большому числу самых разных тестов, имеющих отношение к умственным способностям, были выделены три фактора - общего, вербального и невербального интеллекта. Таким образом, массив в несколько десятков показателей был сведен лишь к одному обобщенному и двум достаточно специфическим. Основной идеей этой математической процедуры является попытка увидеть за многообразием частных проявлений (что типично именно для психологии) некий скрытый смысл или латентные причины, которые и являются первичной базой для объяснения конкретных реакций, измеряемых в эксперименте.

Исходным материалом для факторного анализа становится корреляционная матрица, в результате сложной обработки превращающаяся в специальную таблицу. Строки последней образуются измеренными переменными, а столбцы (число их, как правило, заранее не предсказуемо) обозначают выделившиеся факторы. Основное поле таблицы заполняется цифрами в диапазоне от -1 до +1. Эти цифры называются весом данной переменной, с которым она входит в тот или иной фактор. Чем больший вес (независимо от знака), имеет данная переменная в данном столбце по сравнению с остальными переменными из этого же столбца, тем большую роль она играет в понимании смысла фактора (табл. 1).

Преобразование ваших исходных данных в эту факторную матрицу - дело вычислительной техники. Творческий компонент работы с факторным анализом заключается в интерпретации выделившихся факторов. Как их назвать или какой смысл в них заключен - решаете вы, опираясь на свой профессиональный опыт и перечень признаков, вошедших в данный фактор с максимальными нагрузками. Ар-

Таблица 1

Пример приведения результатов факторного анализа

Переменные	Фактор 1	Фактор 2	Фактор 3
А	-0,309	0,891	-0,326
	-0,661	-0,452	0,355
С	0,813	-0,480	0,037
D	0,077	0,348	0,924
Е	0,774	0,081	-0,413
F	-0,733	-0,378	-0,480
Объяснимая	2,338	1,502	1,489
дисперсия	2,338	1,502	1,489

гументация содержания, фактически угадываемого в том или ином факторе - самая сложная и противоречивая задача. Например, если с большими положительными весами в один из выделившихся факторов вошли такие переменные, как высокий рост, грубый голос, большая мышечная масса, склонность к риску, широкие плечи, агрессивное поведение, то вероятнее всего подобная комбинация антропологом будет трактоваться как фактор мужского пола, эндокринолог увидит влияние какого-то гормона, а психолог попытается найти некие аналоги в типологии личности. Особо широко в психологии приемы факторного анализа представлены при попытках произвести упорядочение (объединение в шкалы) многочисленных пунктов в объемных личностных опросниках.

Большинство программ факторного анализа построено таким образом, что первый выделившийся фактор обладает самым большим влиянием на разброс показателей в группе (объяснимая дисперсия), а значение остальных факторов последовательно убывает.

Существует несколько основных форм факторного анализа, дающих в итоге различные результаты. Выбор необходимого варианта диктуется конкретными задачами дипломного исследования.

❖ Кластерный анализ

Если вам необходимо разбить множество ваших переменных (объектов) на заданное или неизвестное число классов, то целесообразно использовать кластерный анализ (cluster - гроздь, пучок, скопление, группа элементов, характеризуемых каким-либо общим свойством). Это не слишком часто используемая в дипломных работах форма математической обработки эмпирических материалов, представляющая интерес в тех случаях, когда переменных достаточно мно-

Рис. 3. Пример одного из вариантов графического представления результатов кластерного анализа шести переменных.

го и хочется наглядно увидеть их упорядоченность - в каких иерархических отношениях находятся переменные более высокого уровня обобщенности к более конкретным, частным (рис. 3).

Весьма любопытные результаты, тяготеющие к сфере психолингвистики, с помощью кластерного анализа можно получить при применении его к пунктам психологических тестов, вопросам опросников и анкет.

Существует точка зрения, что в отличие от многих других статистических процедур, методы кластерного анализа используются в большинстве случаев тогда, когда еще не имеется каких-либо гипотез относительно классов, т. е. когда вы все еще находитесь в описательной стадии исследования.

Пользоваться результатами кластерного анализа нужно осторожно, поскольку он может навязывать экспериментатору гипотезу об отношениях переменных, построенную на внешних, формальных критериях и не учитывать их качественную специфику. Для того, чтобы избежать подобной ошибки, предпочтительно применять несколько разных алгоритмов расчета (их много, техники группировки отличаются) и выбрать из результатов тот, который лучше всего объясняется с позиции здравого смысла. Следует понимать, что кластерный анализ определяет «наиболее возможно значимое решение».

❖ Дискримииантный анализ

Еще один из методов статистической обработки, который может оказаться полезным в дипломной работе, называется дискриминант- ним анализом. Суть его состоит в том, что он позволяет делить обладающие какими-то признаками объекты или состояния, относя их к како- му-либо классу или оценивать близость конкретного состояния к одному из классов. Сама исследовательская процедура дискриминан- тного анализа состоит из нескольких шагов:

- определяются группы, которые в дальнейшем нужно различать (например, больных истерическим неврозом от больных неврозом навязчивых состояний) - это так называемая обучающая выборка;

- эти группы, каждый член которых уже имеет точный (верифицированный) диагноз, исследуются по максимальному числу признаков (текущая симптоматика, личностная предрасположенность, специфика семейного воспитания, характер психотравмирующих ситуаций и т. п.);

- по каждому из исследованных признаков вся обучающая выборка (и тех и других больных) дискриминируется и отслеживается - насколько точно данный признак разделил группу по диагнозам по сравнению с фактическим положением дел;

- из всех просмотренных признаков отбираются наиболее информативные (те, которые наиболее точно делят обучающую выборку) и в дальнейшем они начинают использоваться для улучшения точности диагноза у тех, кому он еще не поставлен;

- попутно, при необходимости, можно отследить, насколько близко или далеко находится каждый из обследованных индивидов к тому или другому состоянию.

В итоге дискриминантного анализа для каждой переменной вы получите стандартизованный коэффициент (Т - лямбда Уилк- са), интерпретируемый следующим образом: чем он больше, тем меньше вклад соответствующей переменной в различение совокупностей.

Другими словами, основная идея дискриминантного анализа заключается в том, чтобы определить, отличаются ли совокупности по среднему какой-либо переменной (или их комбинации), и затем использовать эту переменную, чтобы предсказать для новых членов их принадлежность к той или иной группе (это задача прогноза). Более простой пример: показатель роста может служить дискриминирующим признаком для отнесения неизвестного нам человека к мужскому или женскому полу, поскольку уже точно известно, что средний рост мужчины выше среднего роста женщины.

Один подобный признак, как можно догадаться из представленного примера, не гарантирует надежности прогноза, но совокупность характеристик может сделать его достаточно уверенным.

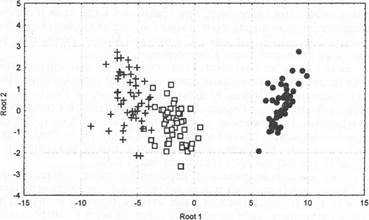
Ниже приводится иллюстрация графического представления дискриминантного анализа (рис. 4).

Root 1 vs. Root 2

Рис. 4. Графический пример разделения носителей признака на три группы, полученный в результате дискриминантного анализа.

❖ Непараметрические методы

Еще раз хотелось бы подчеркнуть, что все рассмотренные процедуры статистического анализа могут быть корректно использованы только в том случае, если ваши экспериментальные данные подчиняются т. н. нормальному закону распределения или хотя бы приближаются к нему. Это значит, что в имеющемся у вас распределении крайние значения признака - и наименьшие и наибольшие - появляются редко, а чем ближе значение признака к средней арифметической, тем чаще оно встречается (см. рис. 1).

Если такого соответствия нет, что, как правило, объясняется либо малыми размерами выборки (менее 20—30), либо измерениями в порядковых шкалах (типа «высокий», «средний», «низкий»), либо тем, что переменные объективно распределены «ненормально», то для обработки эмпирических материалов диплома нужно использовать так называемые непараметрические критерии, хотя они и имеют меньшую мощность и обладают меньшей гибкостью (для их расчета не рассматриваются и не учитываются значения среднего и стандартного отклонения). Но у них есть и ряд преимуществ. Они малочувствительны к неточным измерениям и эти методы могут применяться для обработки данных, имеющих полуколичественную природу (ранги, баллы и т. д.). Кроме того, с их помощью можно получить ответы на такие вопросы, которые неразрешимы с использованием методов, основанных на нормальном распределении. Следовательно, они иногда оказываются уместны и для обработки нормально распределенных результатов исследования.

Не вдаваясь в подробности, укажем лишь на названия непараметрических процедур, позволяющих получить показатели, аналогичные нормально распределенным.

Для выяснения достоверности различий между двумя независимыми выборками (например, при сравнении мальчиков и девочек) непараметрическими альтернативами t-критерия являются серийный критерий В альд а-Вольфович a, U критерий Манна-Уитни и двухвы- бор очный критерий типа Колмогорова-Смирнова.

Если в дипломе выясняются различия между зависимыми выборками (например, показателями одной группы до коррекционной работы и после нее), то нужно использовать Т-критерий Уилкоксона для разностей пар, который может быть применен также и к ранжированным данным. По сравнению с t-критерием Стъюдента, он требует значительно меньшего объема вычислений и почти также строго проверяет нормально распределенные выборки. Его эффективность для больших и малых выборок составляет около 95%.

Если две рассматриваемые переменные имеют альтернативное распределение (включают только две градации, как например, показатели теста в группе ниже или выше некой избранной величины до и после тренировок, либо количество справившихся с контрольной по математике среди мальчиков и девочек), то подходящими непараметрическими критериями достоверности различий будут %² (хи-квадратен не рекомендован к применению, если число опытов в каждом из сравниваемых распределений меньше 10) и точный критерий Фишера для четырехпольной таблицы. Внимание: не путайте алгоритм расчета упомянутого непараметрического критерия %² с имеющим много общего алгоритмом расчета критерия согласия х² Пирсона, полезного при сравнении эмпирического и теоретического распределений, как правило используемого для установления соответствия реально полученного распределения нормальному закону.

Для выяснения связей между признаками (корреляции) можно рассчитать уже упоминавшийся тетрахорический показатель (г), ранговые коэффициенты корреляции Спирмена (R или р) и may (т) Кендалла. Последние два могут быть использованы для определения тесноты связей как между количественными, так и между качественными признаками при условии, если их значения упорядочить или проранжировать по степени убывания или возрастания признака.

❖ Компьютерная обработка и графические иллюстрации

Пускай вас не смущает некоторая перегруженность статистических процедур, рекомендуемых для использования в дипломной работе. В большинстве случаев вам не обязательно (хотя и желательно) быть знакомыми с их математическим аппаратом. К сегодняшнему дню для нужд науки разработаны многочисленные компьютерные программы, позволяющие даже не сведущему в математике человеку довольно легко рассчитывать большинство желаемых показателей. Самыми известными и популярными из них являются пакеты Statistica (табличные и графические примеры с ее использованием приведены выше) и SPSS. Обе программы снабжены справочным материалом в форме Help-ов и специальным информационным сопровождением с обзором основных расчетных алгоритмов. При выведении показателей различия, в корреляционных матрицах и в других таблицах автоматически выделяются цветом и жирностью числовые значения, представляющие для исследователя особый интерес (по достоверности, важности, приоритетности и т. д.).

Эти же пакеты позволяют существенно улучшить внешний вид дипломной работы за счет внесения в нее большей наглядности. Это достигается заменой некоторых трудно читаемых таблиц и цифровых данных на графики, гистограммы, и другие формы иллюстраций, хорошо вписывающихся в смысловую канву предъявленных результатов (но ничего лишнего!).

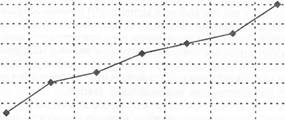
Выбор формы графика не должен быть случаен. Например, изменения во времени лучше воспринимаются в линейном представлении, сопоставление показателей двух групп - в столбчатом, пропорции - в круговых гистограммах, а рассеяние - в точечном (рис. 5—8).

1 -------------------- г— I t |[ ( •

ПН ВТ cp чт пт сб ВС

Рис. 5. Пример линейного графика роста показателя за неделю.

Ш1983 год В1985 год

Рис. 6. Пример столбчатого графика показателей двух групп.

1.3.4.5.3. Общие требования к блоку обсуждения результатов

Второй блок предусматривает обсуждение результатов, которое должно решить две задачи:

- сопоставить полученные вами экспериментальные данные с результатами исследований других авторов (полностью совпадают, частично совпадают, не совпадают, противоречат, либо полученная информация в силу своей новизны и оригинальности несопоставима ни с какими ранее добытыми сведениями);

- определиться, с позиции какой научной теории или концепции могут быть объяснены результаты вашего эксперимента и являются ли положения этой теории исчерпывающими для их понимания.

35,2%

Рис. 7. Пример круговой диаграммы процентного представительства трех частей одной группы.

7,5 6,5 5,5 4,5 3,5 2,5 1.5 0,5

4 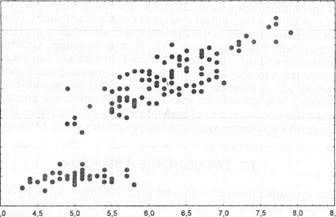5

Рис. 8. Пример графика рассеяния сочетанных характеристик по двум показателям.

Если в предыдущем разделе (или главе) вы демонстрируете себя как добытчик, получатель информации, владеющий методами экспериментального поиска и статистическими технологиями, то здесь, обосновывая будущие выводы, вы выступаете в роли автора и носителя собственных идей.

При обсуждении материала важно не оставить без комментариев все полученные вами факты, способные подтвердить или поставить под сомнение выдвинутую в начале исследования гипотезу. Поэтому, прежде чем начинать обсуждение, из экспериментального раздела необходимо выбрать и в виде кратких тезисов сформулировать (для себя) перечень того, что может «сыграть» на обсуждение. Постарайтесь, чтобы ничто интересное не осталось не замеченным. Убедитесь, что все отобранные

вами экспериментальные факты могут быть сопоставлены с ранее вычитанной литературой и если оказывается, что уже имеющихся источников не хватает, еще раз посетите библиотеку. Обратите внимание, что в данном разделе диплома можно ссылаться не только на работы, упомянутые в литературной обзоре, но и приводить новые, ранее не цитированные.

⇐ Предыдущая 1 2 345 6 7 8 Следующая ⇒