Задача №18. Задача №19. Задача №20

Задача №18

В классе 36 учеников. Каждый мальчик в классе дружит ровно с четырьмя девочками, а каждая девочка – с пятью мальчиками. Сколько в классе девочек и сколько мальчиков?

Решение:

Обозначим через 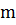и 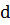число мальчиков, и, соответственно, число девочек в данном классе.

По условию имеем .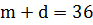

Назовем пару, состоящую из мальчика и девочки, дружной, если они дружат друг с другом.

Тогда, число дружных пар в классе, с одной стороны равно 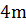, а с другой стороны .

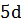Следовательно, .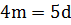

Получили систему из двух уравнений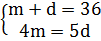

Решив систему, получаем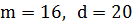

Ответ: 16 мальчиков и 20 девочек.

Задача №19

Произведение 22 целых чисел равно 1. Может ли сумма этих чисел равняться нулю?

Решение:

Произведение целых чисел может равняться 1 только в том случае, если каждое из них равно либо +1 либо -1, причем количество отрицательных сомножителей должно быть четно.

С другой стороны, чтобы сумма 22-ух чисел , каждое из которых равно +1 или -1, равнялась нулю, необходимо, чтобы положительных и отрицательных чисел было поровну, т.е. отрицательных единиц должно быть нечетное количество.

Получили противоречие.

Ответ: не может.

Задача №20

В корзине лежат 30 грибов. Среди любых 12 из них имеется хотя бы один рыжик, а среди любых 20 грибов – хотя бы один груздь. Сколько рыжиков и сколько груздей в корзине?

Решение:

Среди 30 грибов должно быть не менее 19 рыжиков. В противном случае найдется 12 грибов, среди которых нет рыжика.

Аналогично, в корзине не менее 11 груздей, а следовательно рыжиков не более 19.

Поэтому рыжиков в корзине ровно 19, а груздей 11.

Ответ: 19 рыжиков и 11 груздей.

⇐ Предыдущая 1 2 3 4 567 8 Следующая ⇒