Задача №8. Задача №9. Задача №10. Задача №11

Задача №8

По периметру сада растет 20 кустов смородины. Число ягод на соседних кустах отличается на 1. Может ли на всех кустах вместе быть 33 ягоды?

Решение:

Так как число ягод на соседних кустах отличается на единицу, то эти числа разной четности.

Следовательно, кусты с четным числом и кусты с нечетным числом ягод чередуются, т.е. имеются 10 кустов с нечетным числом ягод и 10 кустов с четным числом.

Но тогда сумма всех ягод будет четным числом, так как сумма четного числа нечетных чисел – четна.

Ответ: нет.

Задача №9

Найдите все трехзначные числа, которые в одиннадцать раз больше суммы своих цифр.

Решение:

Пусть 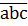– искомое трехзначное число, где 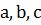– цифры, причем .

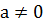Имеем ,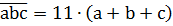

или .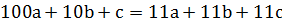

Откуда .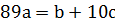

Так как 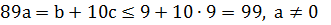, то .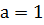

Следовательно, 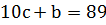, или .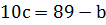

Поскольку 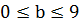, то 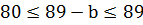, откуда .

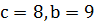Ответ: 198

Задача №10

Верно ли, что при любом 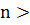1 справедливо неравенство:

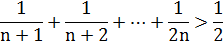
Решение:

Для любого натурального 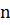в левой части неравенства содержится ровно 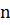слагаемых и каждое из них не превосходит последнего – наименьшего. Таким образом

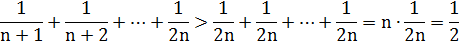
Ответ: нет

Задача №11

Число 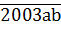делится на 12. Найдите все такие числа.

Решение:

Чтобы 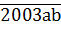делилось на 12 необходимо и достаточно, чтобы оно делилось на 4 и на 3. Необходимость очевидна, а достаточность следует из того, что числа 4 и 3 взаимно простые. Согласно признаку делимости на 3 и учитывая, что 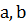– цифры, имеем 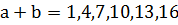. Из признака делимости на 4 (число делится на 4, если двузначное число, образованное его двумя последними цифрами делится на 4) следует, что число 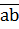должно делиться на 4. Простым перебором находим, что .

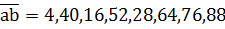Ответ: 200304, 200340, 200316, 200352, 200328, 200364, 200376, 200388.

⇐ Предыдущая 1 234 5 6 7 8 Следующая ⇒