
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Нүкте қозғалысының табиғи тәсілмен берілуі
3 Нүкте қозғалысының табиғи тәсілмен берілуі
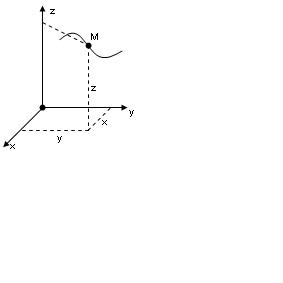
Нүкте қозғалысының берілуінің табиғи тәсілінде нүктенің кез келген бір санақ жүйесіне қатысты траекториясы беріледі. Одан кейін, оның бойынан қандайда болсын бір нүкте О1-ді доға ұзындығын есептеудің бастапқы нүктесі етіп алып, қашықтықты санаудың оң бағыты үшін мүмкін екі бағыттың кез келген бірі алынады. Сонда М нүктесінің орны S=O1M шамасымен анықталады.
А нүктенің траектория бойындағы орнын әрбір уақыт сәтінде де таба алуымыз үшін, доға ұзындығы S=O1M және уақыт t-ның әрбір мәніне сәйкес келетін S-тің мәнін беретін бір сарынды, үздіксіз уақыт функциясы берілуі керек.
 (2.1)
(2.1)
| 2.2-сурет |
3,1 Табиғи үш жақ
| 2.9-сурет |
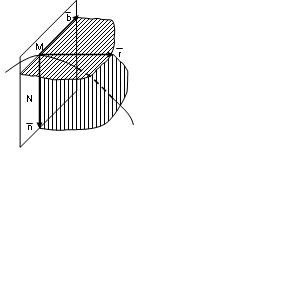 1. Табиғи үш жақ. Табиғи өстер. Траекторияның бір–біріне шексіз жақын орналасқан үш нүктесі арқылы өтетін жа-зықтық, оның ортаңғы нүктесіне жүргізі-лген, жанаспа жазықтық деп аталады.
1. Табиғи үш жақ. Табиғи өстер. Траекторияның бір–біріне шексіз жақын орналасқан үш нүктесі арқылы өтетін жа-зықтық, оның ортаңғы нүктесіне жүргізі-лген, жанаспа жазықтық деп аталады.
Жанамаға перпендикуляр, М нүктесі арқылы өтетін, N-жазықтығы траекто-рияның осы нүктедегі нормаль жазықтығы деп аталады.
Траекторияның М нүктесіндегі жанама арқылы өтетін нормаль және жанаспа жазықтықтарға перпендикуляр үшінші жазықтық траекторияның сол нүктедегі түзулеуші жазықтығы деп аталады (2.9-сурет). Жанаспа жазықтықта жатқан нормаль қисықтың М нүктесіндегі бас нормаль деп, ал жанаспа жазықтыққа осы нүктеде жүргізілген перпендикуляр бинормаль деп аталады. Жанаманың оң бағыты ( 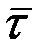 бірлік векторы) қозғалыспен бағыттас келеді. Бас нормальдың оң бағыты (
бірлік векторы) қозғалыспен бағыттас келеді. Бас нормальдың оң бағыты ( 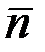 бірлік векторы) траекторияның ойыс жағына қарай бағыт-талады. Бинормальдың оң бағыты (
бірлік векторы) траекторияның ойыс жағына қарай бағыт-талады. Бинормальдың оң бағыты ( 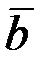 бірлік векторы)
бірлік векторы)  және
және 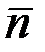 векторларымен оң координаттар жүйесін құрайтындай етіп алынады. Бас нүктесі М болатын бұл координаттар жүйесі М
векторларымен оң координаттар жүйесін құрайтындай етіп алынады. Бас нүктесі М болатын бұл координаттар жүйесі М 
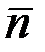
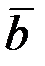 табиғи координаттар жүйесі деп немесе табиғи үшжақ деп аталады. Координаттар жазықтары екі-екіден алынған бірлік векторларымен анықталады. (
табиғи координаттар жүйесі деп немесе табиғи үшжақ деп аталады. Координаттар жазықтары екі-екіден алынған бірлік векторларымен анықталады. (  ,
, 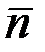 ) –жанаспа жазықтық, (
) –жанаспа жазықтық, ( 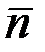 ,
, 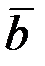 ) – нормаль жазықтық, (
) – нормаль жазықтық, ( 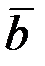 ,
,  ) – түзулеуші жазықтық.
) – түзулеуші жазықтық.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|