тепе теңдігіндегі өзара тәуелсіз i, j, k векторының алдындағы коэффициенттерді теңестіреміз

(2.20)тепе теңдігіндегі өзара тәуелсіз i, j, k векторының алдындағы коэффициенттерді теңестіреміз

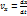
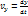
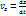(2.21)

(2.21) формулалары нүкте жылдамдығы v ның координатттық остердегі проекцияларын орнектейді. Жылдамдық проекциялары (2.21) табылғаннан кейін вектордың өзі де толық табылады. Оның модулі мына формуламен анықталады.

v= 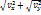+ 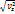(2.22)

Осыдан соң жылдамдық векторының бағыттаушы косинустарын есептей аламыз

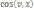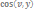= = (2.23)

Қозғалысы координаттық тәсілде берілген нүкте үдеуі

Қозғалмайтын Oxyz координаттар жүйесіндегі нүкте қозғалысы

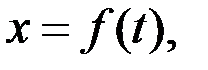
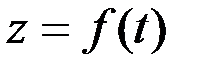(2.24)

теңдеулерімен анықталады дейік. Осы теңдеулер арқылы нүкте үдеуін қалай есептеуге болатынын көрейік. Нүкте үдеуі деп (2.13) не (2.14) векторлық теңдікпен берілген векторды айтамыз. (2.14) теңдіктің оң жағындағы радиус-вектор 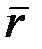-ді координаттар өстеріне жіктеп жазуға болады:

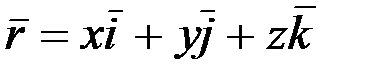. (2.25)

(2.25)-тегі 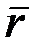векторының компоненттерін (2.14) теңдігіне қойып

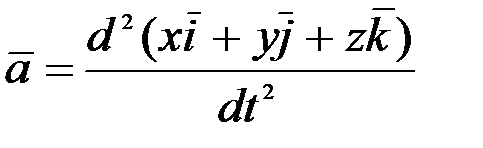. (2.26)

(2.26) теңдігінің оң жағындағы туындыны есептеп шықсақ, мына теңдікке келеміз:

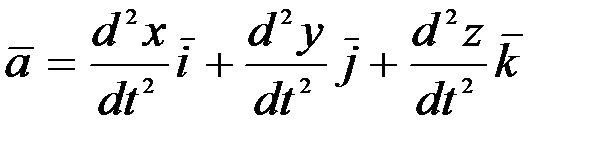. (2.27)

Енді үдеу векторы 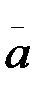-ны үш құраушыға жіктеп оны (2.27) теңдігінің сол жағына қоямыз:

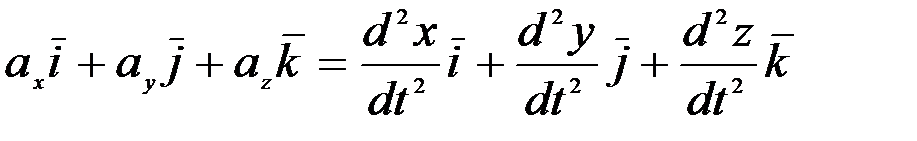. (2.28)

(2.28) теңдігі орынды болуы үшін, бұл теңдіктің екі жағында тұрған өзара тәуелсіз 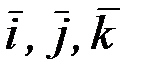бірлік векторларының әрбіреуінің араларындағы коэффициенттері бірі-біріне тең болуы керек:

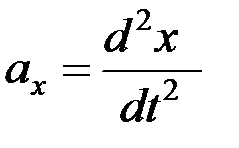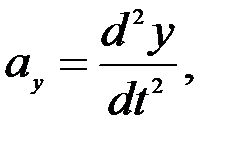
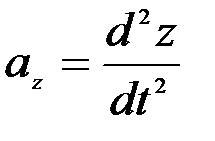, . (2.29)

Үдеу модулі мына формуламен анықталады:

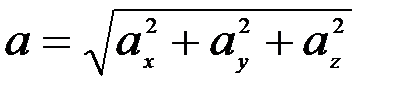. (2.30)

Үдеу векторының кеңістіктегі бағыты оның бағыттаушы косинустарымен анықталады:

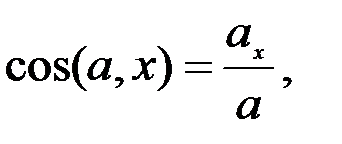
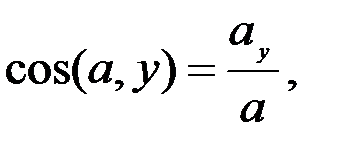
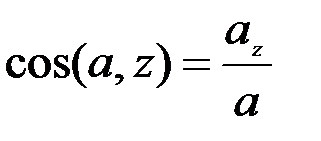. (2.31)

⇐ Предыдущая 1 2 345 6 7 8 9 10 Следующая ⇒