Система сходящихся сил. Значение равнодействующей не зависит от порядка сложения сил.

Система сходящихся сил

Системой сходящихся сил (ССС)называют такую систему сил, линии, действия которых пересекаются в одной и той же точке (рис. 6, а).

Система сходящихся сил имеет равнодействующую R, которая равна геометрической сумме этих сил и проходит через точку пересечения их линии действия. На рис. 6,б показано геометрическое сложение системы сходящихся сил F₁, F₂, F₃ и F₄силы сложены последовательно, в результате сложения получена равнодействующая R. Изменим последовательность сложения сил на следующее F₄, F₁, F₃ и F₂ (рис. 6, в) значение равнодействующей R не изменило.

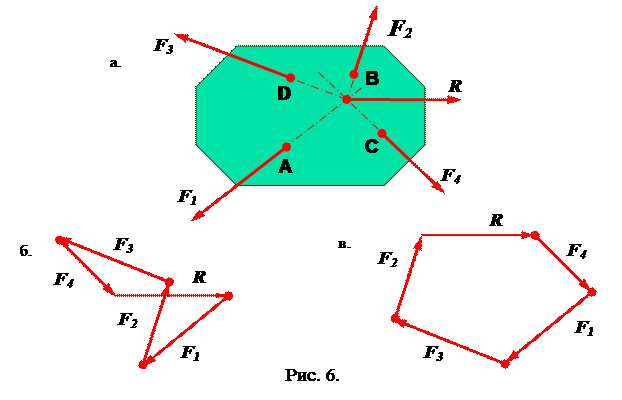
Значение равнодействующей не зависит от порядка сложения сил.

Главным вектором R называется вектор, получаемый путем геометрического сложения ССС.

Разложить силу на составляющие - это означает найти такую CCC, главным вектором которой является исходная сила.

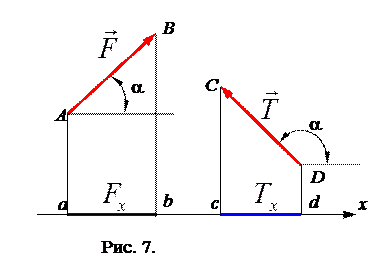
Проекцией силы на ось называется скалярная величина, равная длине отрезка, с соответствующим знаком, заключенного между проекциями начала и конца вектора силы на ту же ось (рис. 7).

Проекция силы равна произведению модуля силы на косинус угла между силой и положительным направлением оси:

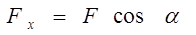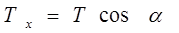
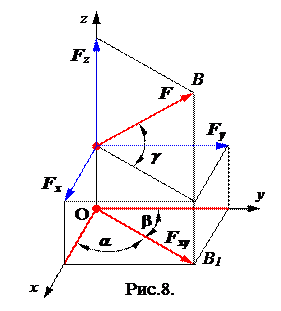Проекция силы F на плоскость это вектор F_ху, заключенный между проекциями начала и конца силы F на эту плоскость (рис. 8). В отличие от проекции силы на ось, проекция силы на плоскость есть величина векторная. По модулю:

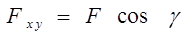где g - угол между направлением силы F и ее проекции F_xy.

Аналитический способ задания силы. Для задания силы аналитическим способом необходимо выбрать систему координатных осей ОXYZ, по отношению к которой будет определяться направление силы в пространстве и задать отдельно точку приложения силы А ее координатами x, у, z. Для решения задач механики удобнее задавать силу ее проекциями F_x, F_y, F_z на координатные оси. Зная эти проекции, можно определить модуль силы F и углы α, β, γ, которые она образует с координатными осями Оx, Оу, Оz, по формулам: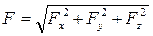

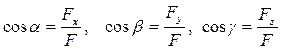
Теорема о проекции вектора суммы: проекция вектора суммы на какую-либо ось равна алгебраической сумме проекций слагаемых векторов на ту же ось:

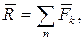
то его проекции на оси:

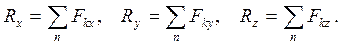
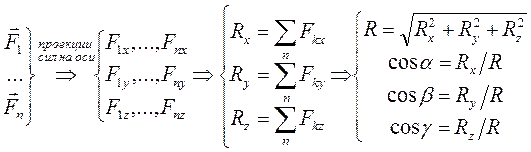Алгоритм задачи о сложении ССС:

⇐ Предыдущая 1 234 5 6 7 Следующая ⇒