Связи и их реакции

Связи и их реакции

Ограничения на свободу перемещений материальных объектов, называются связями.

Сила, с которой связь действует на рассматриваемую точку, систему или твердое тело, называется реакцией связи.

Аксиома об освобождения от связей. Не изменяя движения или равновесия механической системы, можно отбросить наложенные на нее связи, заменяя их действие силами, равными реакциям отброшенных связей.

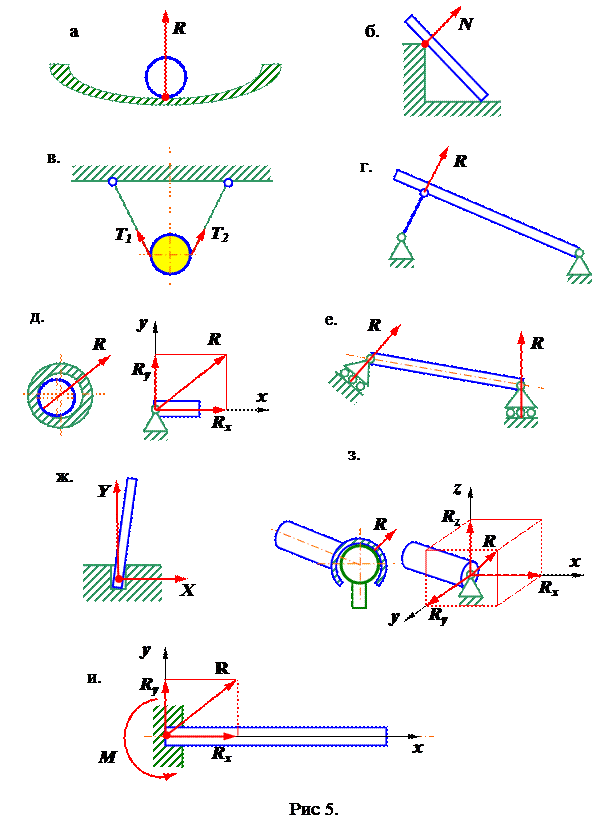
На рис. 5 приведены варианты связей наложенных на систему или твердое тело и показаны направления действия их реакций.

Опора на гладкую поверхность (рис. 5, а) реакция связи направлена перпендикулярно опорной поверхности.

Опорная точка или ребро (рис. 5, б) реакция направлена перпендикулярно опирающейся поверхности.

Невесомая тонкая нить (рис. 5, в) реакция направлена вдоль нити к точке подвеса, то есть нить работает только на растяжение.

Стержень (рис. 5, г) реакция действует вдоль оси стержня, может работать как на растяжение, так и на сжатие.

Неподвижный цилиндрический шарнир (рис. 5, г). Связь позволяет поворот и перемещение относительно оси шарнира, но не позволяет перемещения перпендикулярно оси шарнира. Реакция лежит в плоскости перпендикулярной оси шарнира, ее направление неизвестно, но она может быть представлена двумя взаимно перпендикулярными составляющими.

Подвижный цилиндрический шарнир (рис. 5, д). Связь лежит в плоскости перпендикулярной оси шарнира и направлена через ось шарнира перпендикулярно опорной поверхности.

Подпятник (рис. 5. е) такая связь не позволяет перемещаться точке ни в одном из направлений, но не ограничивает поворот относительно оси подпятника. Направление реакции не определено, но она может быть представлена двумя взаимно перпендикулярными составляющими.

Неподвижный шаровой шарнир (рис. 5, ж) такая связь не позволяет точке перемещаться ни в одном из направлений, но не ограничивает ее повороты относительно осей шарнира. Направление реакции не определено, но она может быть представлена тремя взаимно перпендикулярными составляющими.

Жесткая заделка (рис. 5, з) такая связь не позволяет перемещения и повороты относительно точки. Реакция связи можно представить двумя взаимно перпендикулярными составляющими и реактивным моментом.

Аксиома о наложении новых связей. Равновесие механической системы не нарушится при наложении на нее новых связей.

⇐ Предыдущая 123 4 5 6 7 Следующая ⇒