
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Колебания системы с одной степенью свободы
14.3 Колебания системы с одной степенью свободы
Колебания системы, происходящие при отсутствии внешних возмущаю-щих сил и обусловленные только упругими свойствами системы, называются свободными. Груз Q подвешен к упругому невесомому стержню АВ (рис. 14.3) . Удлиним стержень на величину 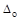 и предоставим тело самому себе. Оно будет совершать колебательные движения в вертикальном направлении. Положение тела определяется одним параметром
и предоставим тело самому себе. Оно будет совершать колебательные движения в вертикальном направлении. Положение тела определяется одним параметром 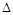 - перемещение тела относительно по-ложения статического равновесия (система имеет одну степень свободы).
- перемещение тела относительно по-ложения статического равновесия (система имеет одну степень свободы).
Так как рассматриваются колебания тела относительно положения стати-ческого равновесия, то влияние собственного веса тела исключается. Реакция
со стороны стержня АВ по закону Гука равна 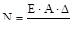
Сила инерции равна
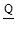
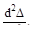
Сумма этих сил должна быть равна нулю:
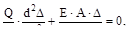
или
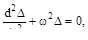
где 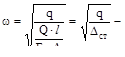 круговая частота колебаний (число колебаний в 2π секунд),
круговая частота колебаний (число колебаний в 2π секунд), 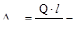 удлинение стержня АВ от статической нагрузки Q.
удлинение стержня АВ от статической нагрузки Q.
Интеграл уравнения: 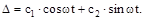
Если при t =0, 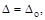
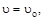 то из уравнения
то из уравнения
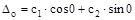
и
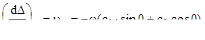
найдём с1= 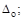
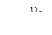
В итоге получаем: 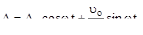
Рассмотрим случай, когда в процессе колебания действует возмущающая сила F(t)=Fмах 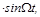 где Fмах и Ω- максимальное значение и круговая частота изменения возмущающей силы соответственно.
где Fмах и Ω- максимальное значение и круговая частота изменения возмущающей силы соответственно.
Уравнение движения без учёта сил сопротивления имеет вид:
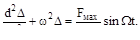
Общий интеграл уравнения (для случая, когда 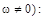
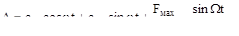
Колебания, обусловленные действием возмущающей силы, называются вынужденными. Их частота равна частоте изменения возмущающей силы.
Наибольшее динамическое перемещение
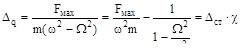 ,
,
где: ω2m = c – коэффициент жёсткости системы (с = 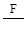 );
);
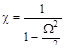 - коэффициент динамичности.
- коэффициент динамичности.
 На рис. 14.4 привязан график зависимости коэффициента динамичности χ от отношения частот. В случае совпадения частот вынужде-нных и собственных (ω
На рис. 14.4 привязан график зависимости коэффициента динамичности χ от отношения частот. В случае совпадения частот вынужде-нных и собственных (ω 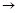 Ω) амплитуда вынужденных ко-лебаний резко возрастает (рис. 14.4, (1)). Это явление носит название резонанса.
Ω) амплитуда вынужденных ко-лебаний резко возрастает (рис. 14.4, (1)). Это явление носит название резонанса.
Реально влияние окружа-ющей среды, внутреннее тре-ние в колеблющемся элемен-те приводит к рассеиванию энергии и кривая (2) описы-вает реальную картину
Явление роста во времени амплитуды колеба-ний при совпадении частот собственных и вынужденных колебаний опасно. Для его
Рис.14.4 устранения прибегают к демп-фированию конструкций, т.е. применяют специальные устройства, увеличива-ющие рассеивание энергии при колебаниях, и коэффициент динамичности мо-жет соответствовать кривой (3).
При выполнении практических расчётов при известном коэффициенте χ , легко определяется величина максимальных динамических напряжений и пе-ремещений в упругих элементах системы.
σq = σст· χ ; уq = уст· χ ,
где под σст и уст понимается то перемещение и напряжение, которые возникали бы при статическом приложении максимального значения возмущающей силы.
Совпадение частот ω = Ω называют условием резонанса, а зону 0.8 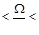 1.2 – зоной критических частот. С помощью конструктивных меро-приятий стараются отстроиться от этой зоны. Более целесообразным является уход в зону уменьшения отношения
1.2 – зоной критических частот. С помощью конструктивных меро-приятий стараются отстроиться от этой зоны. Более целесообразным является уход в зону уменьшения отношения 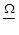 от значения, равного единице. Демп-фирование (постановка амортизаторов – гидравлических, пневматических, пру-
от значения, равного единице. Демп-фирование (постановка амортизаторов – гидравлических, пневматических, пру-
жинных и т. д.) позволяет снизить величину динамических напряжений.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|