Чистый прямой изгиб призматического бруса

10.2. Чистый прямой изгиб призматического бруса

Задаются следующие условия: 1) волокна, параллельные оси бруса, испытывают равномерное растяжение или сжатие, переменное по высоте сечения; 2) деформации сдвига, касательные напряжения, поперечные силы и крутящий момент равны нулю; 3) сечения, плоские и нормальные к оси бруса до изгиба, остаются и после изгиба плоскими и нормальными к изогнутой оси бруса (гипотеза плоских сечений); следовательно, все волокна имеют общий взаимный угол поворота поперечных сечений и общий центр кривизны (рис.10.3); dv/dx = k_x = const, хотя точные значения кривизны 1/ρ дуг концентрических окружностей неодинаковы; 4) физический закон − закон Гука для одноосного напряженного состояния; 5) из трех внутренних усилий, связанных с нормальными напряжениями, задана величина M_z; N = 0; M_y = 0.

Для определения характеристик изогнутого бруса k_х, ε_х, σ_х и u имеем следующие зависимости:

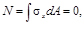
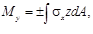
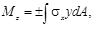
k_х= d²v / dx², k_x= –∂ε_х/ ∂y, σ_х=Eε_х.

За основное неизвестное принимаем k_х. Так как ε_х– функция одной переменной у, то

k_x= – dε_х / dy .

Следовательно,

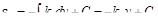
Совместим границу между растянутыми и сжатыми волокнами (нейтральный слой) с координатной плоскостью у = 0, т.е. положим ε_х= 0 при у = 0. В таком случае С = 0 и

ε_х = –k_xy.

Согласно физическому закону

σ_х = –Ek_xy.

В результате подстановки σ_х в интегральные формулы для внутренних усилий получаем

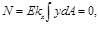
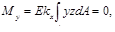
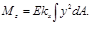
В правой части третьей формулы принят плюс, так как в данном случае изгибающий момент и кривизна имеют одинаковые знаки.

В первой формуле интеграл 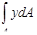выражает статический момент площади сечения относительно оси z. Равенство его нулю свидетельствует о том, что ось z, в точках которой ε_х = 0, проходит через центр тяжести сечения. Согласно физическому закону на этой оси σ_х = 0. Следовательно, ось z есть линия нулевых напряжений при изгибе в плоскости ху. Она называется нейтральной осью сечения (нулевой линией). По обе стороны от нее нормальные напряжения имеют противоположные знаки и нарастают по единому линейному закону, образуя зоны растяжения и сжатия.

Во второй формуле интеграл 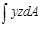выражает центробежный момент инерции сечения относительно осей у и z. Равенство его нулю свидетельствует о том, что оси у и z – главные оси инерции сечения.

Таким образом, определение оси z как главной центральной оси инерции сечения вносит ясность в расположение нейтрального слоя, который был совмещен с координатной плоскостью у = 0, и в ориентацию плоскости действия момента M_z, перпендикулярной оси z и естественным образом проходящей через вторую главную ось – у (признак прямого изгиба).

Переписав третью интегральную формулу в виде

M_z = Ek_xI_z,

где I_z – осевой момент инерции площади сечения, находим

k_x = M_z/(EI_z).

Окончательные выражения деформаций и напряжений имеют следующий вид:

ε_х= – (М_zу)/(EI_z) , σ_х= – (М_zу)/I_z.

Минус поставлен для согласования знаков линейной деформации (напряжения) и изгибающего момента. При у > 0 положительному моменту соответствует отрицательное значение деформации (напряжения).

Пренебрежение влиянием поперечных деформаций ε_y = ε_z= – vε_x на прогибы равносильно принятию для всех волокон прогибов, присущих нейтральному осевому волокну.

Приравнивая правые части k_x=d²v/dx²и k_х=М_z/(EI_z), получаем дифференциальное уравнение изогнутой оси бруса:

d²v/dx²= М_z/(EI_z).

Его интегралы:

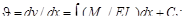
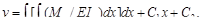
При М_z= const и I_z= const получаем

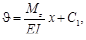
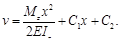
С₁, и С₂ находятся из граничных условий для v и .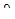

Следует обратить внимание на то, что волокно изгибается по параболе, а не по дуге окружности. Такой результат согласуется с исходным условием и является следствием использования не точного, а приближенного выражения кривизны изгиба.

Анализ полученного решения приводит к следующим выводам:

1. Напряжения σ_х не меняют своего закона по длине бруса и являются функцией только координаты у. На торцах на основании статического граничного условия они трансформируются в распределенную по закону пло-скости нагрузку X_p (рис.10.4), которая и соответствует

Рис.10.4 рассмотренной деформации чистого изгиба. Независи-мость σ_х от х справедлива при I_z= const. Таким образом, чистый изгиб возмо-жен лишь в случае призматического бруса.

2. Кривизна и деформация обратно пропорциональны величине ЕI_z, называемой жесткостью при изгибе.

⇐ Предыдущая 35 36 37 38 394041 42 43 44 Следующая ⇒