ИЗГИБ. Плоский изгиб волокна

10. ИЗГИБ

10.1 . Плоский изгиб волокна

Рассмотрим волокно ab, параллельное оси х. В результате изгиба прямое волокно искривляется (рис.10.1, а). Изгиб волокна сопровождается попереч-ными перемещениями (прогиба-ми) v и углами поворота (девиа-циями) 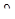его линейных элемен-тов. Углы 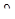– углы наклона каса-тельных к искривленному волок-ну.

При малых перемещениях длина хорды волокна l₁ мало

Рис. 10.1 отличается от первоначальной длины волокна l. Поэтому можно принять l₁= l, т.е. пренебречь продольными перемещениями u (рис.10.1, б). В то же время длина искривленного волокна считается равной длине первоначального прямолинейного волокна.

В пределах малых перемещений допустимо считать 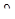≈tg 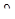и принять 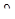=dv/dx.

Поперечные сечения волокна сохраняют прямые углы с касательными к оси волокна после его деформирования. Поэтому углы 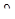характеризуют в то же время повороты поперечных сечений. Вследствие их неодинаковости образуются взаимные повороты с углами 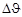. Отношение 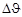к отрезку кривой ∆s между сечениями определяет среднюю кривизну изгиба в точке

k_xm = ∆ 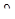/∆s.

При малых углах поворота (∆s ≈ ∆x)

k_xm = ∆ 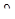/∆x.

Устремляя ∆s и ∆x к нулю, в пределе получаем

k_x= d 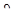/ds и k_x= d 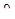/dx

(точное и приближенное значения кривизны изгиба в точке).

Очевидно, что

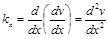Имеется другое определение кривизны: k_x= 1/ρ – 1/r₀, где r₀(ρ) – радиус кривизны до (после) деформирования волокна. Для прямого волокна r₀= ∞ и k_x= 1/ρ.

Из дифференциальной геометрии известно, что

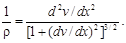
При малых углах поворота ( 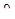= dv/dx) величиной (dv/dx)² можно пренебречь по сравнению с единицей. Тогда

1/ρ ≈ d ²v/dx ².

Итак, формула k_x = d²v/dx² дает приближенное значение кривизны при изгибе.

Величины v, 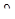и k_x характеризуют изгиб волокна. Если за основную величину принять k_x, то другие характеристики можно получить с помощью интегрирования:

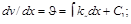
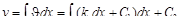
или

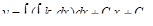
C₁ и C₂ находятся из граничных условий для прогибов и углов поворота. Их смысл легко обнаружить, если положить k_x= 0. Тогда С₂+C₁x – уравнение прямой линии, в котором С₂– поперечное поступательное перемещение линии, а С₁ – ее поворот.

Установим связь между характеристиками изгиба волокна и компонентами деформации в точке. Рассмотрим изгиб волокна, параллельного оси х, с бесконечно малым поперечным сечением dz x dy (рис. 10.3). Пусть в точке С линейная деформация равна ε_x, а в точке А – ε_x+(∂ε_x / ∂у)dу.

Рис.10.2 Рис.10.3

Взаимный поворот линейных элементов АС и BD равен

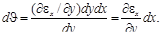
Кривизна волокна

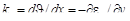
Знак минус поставлен для согласования положительной кривизны и отрицательной производной ∂ε_x / ∂y.

⇐ Предыдущая 34 35 36 37 383940 41 42 43 Следующая ⇒