Плоское напряженное состояние

4.2. Плоское напряженное состояние

В общем случае при переходе из одной точки в другую главные напряжения изменяются непрерывно по величине и направлению. Случай, когда одно из главных напряжений становится равным нулю, называют плоским (двухосным) напряженным состоянием в точке. В соседних точках тела напряженное состояние может быть пространственным (трехосным).

Встречаются и такие случаи, когда во всех точках тела напряженное состояние плоское и при этом площадки с нулевым главным напряжением параллельны друг другу. В таком случае все тело испытывает плоское напряженное состояние. Примером может служить пластинка, подверженная воздействию поверхностной и (или) объемной нагрузки, распределенной равномерно по толщине. При этом равны нулю главные напряжения на площадках в плоскости пластинки, а два других отличны от нуля и, вообще говоря, изменяются при переходе из одной точки в другую.

Три независимые скалярные величины, соответствующие составляющим напряжений, определяют тензор напряжений:

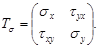
Для определения главных напряжений представляет интерес исследование напряжений, действующих лишь на площадках, перпендикулярных к главной площадке с нулевым главным напряжением. Рассмотрим прямую призму с основанием ВСD высотой dz (рис.4.2).

Уравнения равновесия запишем в виде проекции сил на направления σ_α и τ_α: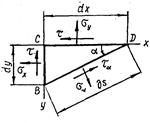

σ_αdzds – (σ_ydzds cosα) cosα– (τdzds cosα)sinα –– (σ_xdzds sinα) sinα – (τdzds sinα) cosα = 0,

τ_αdzds + (σ_ydzds cosα) sinα – (τdzds cosα) cosα –– (σ_xdzds sinα) cosα + (τdzds sinα) sinα= 0.

После сокращения на dzds и преобразо-вания получим

σ_α = σ_xsin²α + σ_ycos²α+τsin2α;

τ_α= 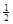(σ_x – σ_y)sin2α+ τcos2α. Рис. 4.2

Чтобы определить положение главных площадок, следует либо приравнять нулю производную dσ_α/dα, либо положить равными нулю касательные напряжения τ_α ввиду их отсутствия на главных площадках. В обоих случаях

получаем следующее уравнение для угла наклона главных площадок (α₀):

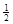(σ_x – σ_y) sin2α₀+ τcos2α₀ = 0 ,

откуда

tg2α₀= 2τ /(σ_у– σ_х) ,

чему соответствуют углы α₀′ и α₀′+ 90°, которые определяют две взаимно перпендикулярные площадки.

Исследуя вторую производную d²σ_α/dα², можно убедиться, что на главной площадке под углом α₀′ при σ_y >σ_x действует максимальное главное напряжение σ₁ ,а на площадке под углом α₀′+ 90° действует минимальное главное напряжение σ₂.

Для определения главных (экстремальных нормальных) напряжений отразим значение угла α₀ в выражении σ_α, используя при этом формулы для sin2α₀, соs2α₀, соs²α₀, sin²α₀, приведенные в п.3.4. В итоге

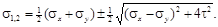
Если одно из напряжений σ_x или σ_y равно нулю, то формула примет вид

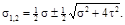
Экстремальные касательные напряжения можно выразить через главные напряжения: ± 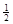( σ₁− σ₂), что соответствует выражению

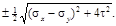
Они действуют на площадках, наклоненных к главным под углом 45° и направлены от σ_min к σ_max (рис.4.3). В общем случае на этих площадках σ_α ≠ 0.

Если оси х и у совмещены с главными осями 1 и 2, то

σ_α = σ₁sin²α + σ₂cos²α ;

τ_α= 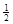(σ₁ − σ₂)sin2α.

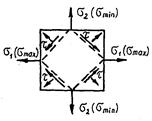При α = 45° и σ₂ = −σ₁ = −σ имеем τ_α = σ, σ_α= 0. Такое напряженное состояние называется чистым сдвигом, а площадки – площадками чистого сдви-га.

В случае σ₁ = σ₂ = σ на всех площадках, проходящих через исследуемую точку, τ_α = 0, σ_α = σ. Такое напряженное состояние называется равномерным двухосным растяжением (или сжатием). Рис. 4.3

При одноосном напряженном состоянии (σ₂ = σ₃ = 0) имеем

σ_α = σ₁sin²α; τ_α= 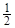σ₁sin2α.

Экстремальные касательные напряжения равны ± σ₁ /2.

⇐ Предыдущая 8 9 10 11 121314 15 16 17 Следующая ⇒