Зависимости между моментами инерции относительно

3.3. Зависимости между моментами инерции относительно

параллельных осей

При известных величинах моментов инерции относительно осей z и у опре-

делим моменты инерции относительно других осей z₁ и y₁, параллельных задан-ным (рис.3.5). Пользуясь общей формулой для осевых моментов инерции, находим

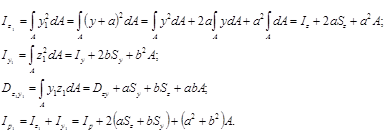
Если оси z и y центральные, то 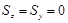, и

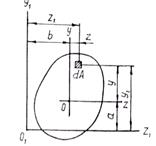
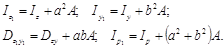
Из полученных формул видно, что моменты инерции относительно центральных осей (когда 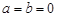) имеют наименьшие значения по сравнению с моментами инерции относительно любых других параллельных осей.

Рис. 3.5

3.4 Главные оси и главные

моменты инерции сечения

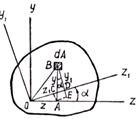
Исследуем изменение моментов инерции при повороте осей координат. При известных величинах моментов инерции относительно осей z и у (не обязательно центральных) определим моменты инерции относительно осей z₁ и y₁, повернутых относительно заданных на угол α (рис.3.6). Координаты площади dA в осях z₁,y₁ выражаются че рез координаты z, у следующим образом:

Рис. 3.6

z₁ = OC + CD = OC + AE = z cosα + y sinα;

y₁ = BE – DE = BE – CA = y cosα – z sinα.

Подставим эти значения в исходные выражения моментов инерции:

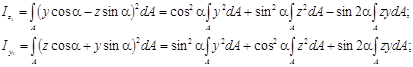
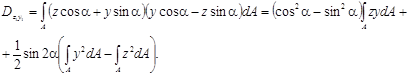
Уяснив смысл интегралов, окончательно находим

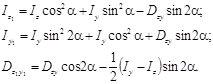
С изменением угла поворота осей координат α каждый из моментов инерции I_z и I_y меняется, а сумма их, равная I_p, остается неизменной. Очевидно, существует такое значение α₀, при котором один из моментов инерции достигает своего максимального значения, в то время как другой принимает минимальное значение. Для определения экстремума приравняем нулю первую производную от I_z₁ и положим α = α₀:

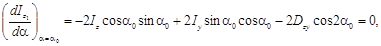
или

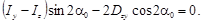
Выражение в левой части представляет собой не что иное, как 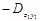. Оси, относительно которых осевые моменты инерции принимают экстремальные значения (при этом центробежный момент инерции становится равным нулю), называют главными осями инерции сечения. Для их определения используют зависимость, получаемую из последнего уравнения:

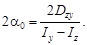
Поскольку формула дает два значения угла α₀′ иα₀″ = α₀′+90º, то существуют две взаимно перпендикулярные главные оси. Соответствующие им моменты инерции называют главными моментами инерции сечения. Ось максимума всегда составляет меньший угол (α₀′) с той из осей (z или у), относительно которой осевой момент инерции имеет большее значение. Напомним, что положительные углы откладываются от оси z против хода часовой стрелки.

Для определения главных моментов инерции отразим значение углаα₀ в выражении 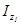, используя при этом формулы тригонометрии:

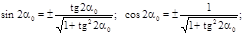
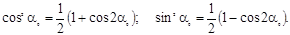
После несложных преобразований получим

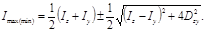
Эта формула позволяет вычислить главные моменты инерции, не определяя положение самих главных осей.

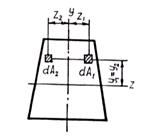Равенство нулю центробежного момента инерции относительно главных осей часто используют для их непосредственного определения. Так, например, для симметричной фигуры ось симметрии является главной осью, поскольку центробежные моменты инерции площадок dA₁ и dA₂ (рис.3.7) при z₂ = –z₁ в сумме дают нуль, в силу чего и для всего сечения величина D_zy равна нулю. Таким образом, одна главная ось – ось симметрии у, другая перпендикулярна ей. Главные оси инерции можно провести через любую точку, взятую в плоскости сечения. Однако практическое значение для расчета элементов конструкций имеют лишь главные центральные оси инерции, проходящие через центр тяжести сечения, который совпадает с осью бруса (стержня) и является центром приведения внутренних

сил. Для прокатных профилей положение глав-ных осей и величины главных центральных момен-тов инерции даны в таблицах сортамента.

Рис.3.7

⇐ Предыдущая 4 5 6 7 8910 11 12 13 Следующая ⇒