
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Вопросы для повторения. Контрольные тесты
Вопросы для повторения
1.Дайте определение понятия «напряжение». Какие виды напряжения различают?
2.Что называют касательным и нормальным напряжением?
3.Какова размерность напряжений?
4.Что обозначают индексы касательного напряжения?
5.Какова зависимость между полным, нормальным и касательным напряжением в точке данного сечения?
6.Как связаны напряжение и внутренние силовые факторы?
7.Какие виды деформаций связаны с каждым из внутренних силовых фак-торов?
8.Чем характеризуют напряженное состояние в точке?
9.Как формулируется закон парности касательных напряжений?
10. Какие площадки называют главными?
11.Чему равны касательные напряжения на главных площадках?
12.Как обозначают главные напряжения? Каково между ними соотноше-ние?
13.Как изменяются величины 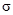 и
и 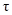 при повороте площадки на угол
при повороте площадки на угол 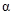 в случае плоского напряженного состояния?
в случае плоского напряженного состояния?
14.Дайте определение линейного, плоского, объемного напряженного сос-тояний используя понятия «главные площадки».
15.Как определить экстремальную величину касательных напряжений, зная напряжения σх, σу, τ в случае плоского напряженного состояния?
16.Как ориентированы площадки в которых действуют τэкстр. по отношению к главным?
17.Какие деформации называют линейными и какие угловыми?
18.Как определяется относительное изменение объема деформированного тела?
Тесты для повторения
1. Как изменится угол αо, если горизонтальная компонента нормального напря-жения изменит направление на противоположное (при условии, что σх >σу)?
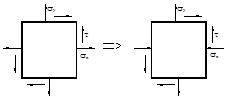 (а) уменьшится, но сохранит знак;
(а) уменьшится, но сохранит знак;
(б) возрастёт, но сохранит знак;
(в) уменьшится и изменит знак;
(г) возрастёт и изменит знак.
Ответ: (а), поскольку в первом случае
tg2 αо= 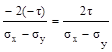 , а во втором tg2 αо=
, а во втором tg2 αо= 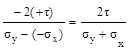 .
.
2. Для случая линейного напряжённого состояния (частный случай объёмного, когда два главных напряжения равны нулю) число главных площадок равно:
(а) 1; (б) 2; (в) 3; (г) бесконечное множество.
Ответ: (г), поскольку площадка, перпендикулярная действующему главному напряжению определена в пространстве, а две взаимно перпендикулярны пер-вой и одновременно перпендикулярны между собой, то они могут иметь беско-нечное число положений.
3. Как изменится сумма нормальных напряжений на любых двух взаимно пер-пендикулярных площадках при плоском напряжённом состоянии, если площад-ки повернуть по часовой стрелке относительно главных?
(а) возрастёт; (б) не изменится; (в) уменьшится; (г) станет равным нулю.
Ответ: (б), поскольку сумма нормальных напряжений в двух взаимно перпен-
дикулярных площадках равна сумме главных напряжений, то для любой пары
взаимно перпендикулярных площадок это сохраняется.
4. Для случая чистого сдвига наименьшее из трёх главных напряжений равно:
(а) σ3 = τ; (б) σ3 = 0; (в) σ3 = -τ; (г) σ3 = σ1.
Ответ: (в), так как в главных площадках при плоском напряжённом состоянии σгл= ± τ, т.е. σ3 равно наименьшему значению (алгебраически).
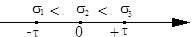
5. Чему равны экстремальные значения касательных напряжений, если извест-но, что одно главное растягивающее напряжение равно 40 МПа, а второе, сжи-мающее равно 60 МПа?
(а) 50 МПа (б) -10 МПа; (в) 40 МПа; (г) –20 МПа.
Ответ: (а), поскольку установлено, что τα= 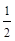 (σ1-σ3) sin2α, то экстремальное значение τ примет при sin2α =1(α=45
(σ1-σ3) sin2α, то экстремальное значение τ примет при sin2α =1(α=45 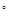 ), а величина τэкстр.=
), а величина τэкстр.= 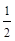 (40-(-60))= 50МПа.
(40-(-60))= 50МПа.
Контрольные тесты
- Для внутренних усилий установите соответствие:
(а) ΜZ= ; (б) MY= ; (в) QY= ; (г) QZ = .
(д) = 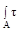 ХZdA;
ХZdA;  (е) =
(е) = 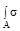 Х ZdA; (ж) =
Х ZdA; (ж) = 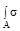 Х YdA; (з) =
Х YdA; (з) = 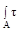 ХYdA.
ХYdA.
2. Сколько независимых скалярных величин, соответствующих составляю-щим напряжений по трем взаимно ортогональным площадкам определяют тен-зор напряжений? 
(а) 4 ; (б) 6 ; (в) 9 ; (г) 12.
3. По какой из приведенных формул определяют главные напряжения при плоском напряженном состоянии?
(а)σx·sin2α+σy·cos2α+τsin2α; (б) 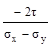 ;
;
(в) 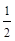 (σx –σy) sin2αо+ τ cos2αо ; (г)
(σx –σy) sin2αо+ τ cos2αо ; (г) 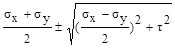 .
.
4. По какой из приведенных формул определяют величину угла αо и его знак (σα >σβ) ?
(а) tg2 αо = 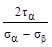 ; (б) tg2 αо =
; (б) tg2 αо = 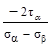 ;
;
(в) tg2 αо = 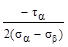 ; (г) tg2 αо =
; (г) tg2 αо = 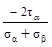 ;
;
5. В площадках чистого сдвига касательные напряжения τ:
(а) равны σ; (б) экстремальны; (в) равны нулю; (г) равны 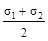 .
.
6. Сколько главных площадок можно выделить вблизи точки в общем слу-чае (объемное напряженное состояние)?
(а) одну; (б) шесть; (в) три; (г) бесконечное множество.
7. В случае плоского равноосного растяжения, сколько главных площадок можно выделить?
(а) две; (б) три; (в) одну; (г) бесконечное множество.
8. Для указанных плоских напряженных состояний (а,б,в,г) – установите соответствие для главных напряжений (д,е,ж,з) и угла αо (и,к,л,м)
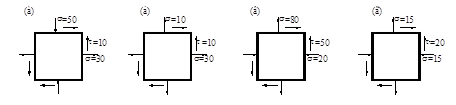
(д) (34.1 ; 5.9) (е) (100.7 ; -40.7) (ж) 31.2 ; -51,2) (з) (25 ; -25)
(и) –22.5 (к) –26.5  (л) +22.5
(л) +22.5 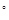 (м) +7
(м) +7
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|