Моменты инерции простейших фигур

3.2. Моменты инерции простейших фигур

Прямоугольник. Определяя элементарную площадь dA в виде произведе-ния bdy или hdz (рис.3.2,а,в), вычисление 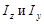сводим к интегрированию по одной переменной:

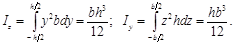
Момент инерции параллелограмма (рис.3.2,б) относительно центральной оси z, параллельной основанию b, определяется также по формуле

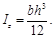
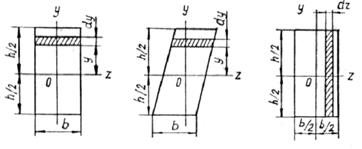а б в

Рис. 3.2

Это следует из того, что момент инерции фигуры не меняется от перемеще-ния ее частей параллельно той оси, относительно которой определяется эта характеристика (а именно так из прямоугольника образован параллелограмм).

Однако момент инерции параллелограмма относительно оси у нельзя вы-числить по формуле для прямоугольника, так как в этом случае элементарные

площадки сдвинуты непараллельно оси у.

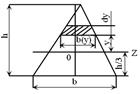Треугольник. Найдем момент инерции I_z отно-сительно оси, проходящей через центр тяжести (рис.3.3). Очевидно, ширина элементарной полоски, находящейся на расстоянии у от оси z, равна:

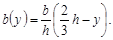
Следовательно, Рис. 3.3

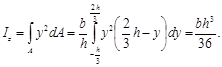
Круг. Вычислим полярный момент инерции круга радиусом r (рис.3.4). Элементарная площадь, вырезанная двумя радиусами и двумя окружностями, равна dA = ρdφdρ. Интегрирование по всей площади заменяется двойным интегрированием:

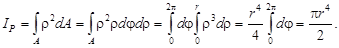
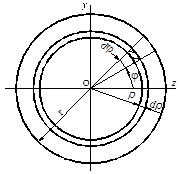Учитывая, что полярный момент инерции равен сумме двух осевых моментов, и принимая во внимание осевую симметрию, получаем

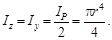
Моменты инерции кольца находим как разность моментов инерции двух кругов – наружного (радиус r_e) и внутреннего (радиус r_i):

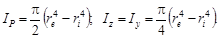
Рис.3.4

⇐ Предыдущая 3 4 5 6 789 10 11 12 Следующая ⇒