
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Ответ: (г) так как Sх > Sy поскольку элементарные площадки удалены на расстояния, большие чем от оси “у”, а из осей х1, х2, х3 статический момент имеет большую величину для наиболее удалённой оси. . Контрольные тесты
Ответ: (г) так как Sх > Sy поскольку элементарные площадки удалены на расстояния, большие чем от оси “у”, а из осей х1, х2, х3 статический момент имеет большую величину для наиболее удалённой оси.
3. Если Jy=Jz , а D yz=0, то оси “y”,”z” являются:
(а) центральными; (б) главными центральными;
(в) осями симметрии; (г) главными.
Ответ: (г), потому что равенство центробежного момента инерции нулю – необходимое и достаточное условие для главных осей инер-ции. Если оси “y”,”z” были бы центральными, то необходимо в дополнение что бы Sy=0 и Sz=0.
4. При повороте взаимно перпендикулярных осей “y”и”z” относительно общего начала координат сумма осевых моментов инерции (Jy+Jz):
(а) зависит от угла поворота; (б) не изменяется;
(в) равна нулю; (г)изменяется, но не зависит от угла поворота.
Ответ: (б) сумма осевых моментов относительно двух ортогональных осей при их повороте остаётся постоянной величиной, равной полярному моменту инерции Jр= 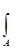 ρ2 dA.
ρ2 dA.
5. Ось “y” изменила своё направление на противоположное. Значение какого момента инерции изменится:
(а) Jy; (б) Jz; (в) Dyz; (г) Jp;
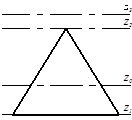 Ответ: (в), величина центробежного момента сохранится, но знак изменится на противоположный. Для других моментов инерции “x”,”y”, координаты стоят под интегралом в квадрате, следовательно будет координата “+y” или ”-у” – величина момента не изменится.
Ответ: (в), величина центробежного момента сохранится, но знак изменится на противоположный. Для других моментов инерции “x”,”y”, координаты стоят под интегралом в квадрате, следовательно будет координата “+y” или ”-у” – величина момента не изменится.
6. Осевой момент инерции для треугольника будет максимальным для:
(а) z0; (б) z1;  (в) z2; (г) z3;
(в) z2; (г) z3;
Ответ: (г), поскольку наименьшее значение осевой момент Jz имеет для центральной оси z0, а значение осевого момента инерции для оси, параллельной цен-тральной возрастает на величину равную произведе-
нию площади фигуры на квадрат расстояния между осями.
Контрольные тесты
1.Если Jy=Jz и Dzy=0, то главные оси инерции наклонены к исходным осям под углом:
(а) α = 90˚; (б) α = 30˚; (в) α = 45˚; (г) α = 60˚;
2. Выражение центробежного момента инерции плоского сечения относительно осей “y”и “z” имеет вид:
(а) 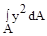 ; (б)
; (б) 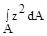 ; (в)
; (в) 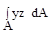 ; (г)
; (г) 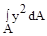 +
+ 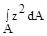 .
.
3. Центробежный момент инерции сечения относительно главных осей:
(а) Dzy > 0; (б) Dzy=0; (в) Dzy < 0; (г) Dzy  0.
0.
4. Осевой момент инерции круглого сплошного сечения определяется по формуле:
(а) 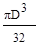 ; (б)
; (б) 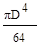 ; (в)
; (в) 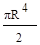 ; (г)
; (г) 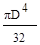 .
.
5.Положение главных осей инерции определяется углом α0, а tg 2α0 равен:
(а) 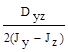 ; (б)
; (б) 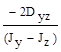 ; (в)
; (в) 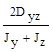 ; (г)
; (г) 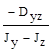 .
.
6.Осевой момент инерции треугольника высотой h и основанием b относительно оси “z”, проходящей через основание определяется по формуле:
(а) 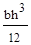 ; (б)
; (б) 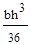 ; (в)
; (в) 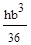 ; (г)
; (г) 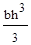 .
.
7.Если Jy < Jz , то при повороте осей на угол α0 главная ось инерции, ближайшая к оси “z” будет осью:
(а) симметрии; (б) максимума; (в) минимума; (г) нейтральной.
8. При повороте осей на угол α, осевой момент инерции Jy, относительно повёрнутой оси “y”, можно вычислить по формуле:
(а) Jz cos2α + Jy sin2α - Dyz sin2α; (б) Jy cos2α + Jz sin2α + Dyz sin2α;
(в) Dyz cos2α - 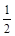 (Jy-Jz) sin2α; (г) Jz cos2α + Jy sin2α - Dyz sin2α
(Jy-Jz) sin2α; (г) Jz cos2α + Jy sin2α - Dyz sin2α
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|