
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Перемещения и деформации
4.3. Перемещения и деформации
Твердое тело, как правило, закреплено. В таком случае перемещение точки тела вызывается только его деформированием. Это перемещение характеризуется вектором 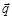 с проекциями u, v, w на оси x, у, z, являющимися функциями координат: u = u(x, у, z), v = v(x, у, z), w = w(x, у, z). В силу сплошности тела эти функции и их частные производные требуемого порядка по x, у, z непрерывны, кроме, возможно, особых точек, линий или поверхностей.
с проекциями u, v, w на оси x, у, z, являющимися функциями координат: u = u(x, у, z), v = v(x, у, z), w = w(x, у, z). В силу сплошности тела эти функции и их частные производные требуемого порядка по x, у, z непрерывны, кроме, возможно, особых точек, линий или поверхностей.
Элементарный параллелепипед, вырезанный в окрестности какой-либо точки, деформируется таким образом, что изменяется длина его ребер и искажаются первоначально прямые углы между гранями, т.е. изменяются объем и форма.
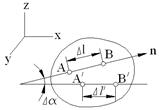 Для определения линейной деформации в точке А вдоль оси n (рис.4.4) возьмем в теле на этой оси малый отрезок АВ длиной ∆l. После деформирования тела он обратится в отрезок А'В', составляющий с отрезком АВ угол ∆α, и будет иметь длину ∆l'. Исходя из незначительного изменения геометрических характеристик тела в результате деформирования, можно считать Рис. 4.4
Для определения линейной деформации в точке А вдоль оси n (рис.4.4) возьмем в теле на этой оси малый отрезок АВ длиной ∆l. После деформирования тела он обратится в отрезок А'В', составляющий с отрезком АВ угол ∆α, и будет иметь длину ∆l'. Исходя из незначительного изменения геометрических характеристик тела в результате деформирования, можно считать Рис. 4.4
угловое перемещение (угол поворота) ∆α малым по сравнению с единицей, так что cos∆α ≈ 1. Величина ∆λ = ∆l' – ∆l представляет собой абсолютное изменение первоначальной длины отрезка АВ. Величина ∆λ/∆l есть средняя линейная деформация вдоль оси n в точке А.
Уменьшая размеры отрезка, в пределе получаем
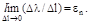
Безразмерная величина εn есть истинная линейная деформация вдоль оси n в точке А.
Полагая, что λ − непрерывная функция l, получим
εn = ∂ λ /∂l.
Если λ зависит от одной переменной l, то
εn = dλ /dl.
Для определения деформации сдвига в точке А в плоскости mn возьмем на этой плоскости два малых отрезка АВ и АС, пересекающихся в точке А под углом 90°. После деформирования тела они обратятся в отрезки А'В' и А'С' с
иным углом пересечения и расположатся в другой плоскости m'n', составляющей с первоначальной угол ∆α. Принимая, как и раньше, cos∆α ≈ 1, определим деформацию сдвига как разность величин углов В'А'С' и ВАС. Наложим угол В'А'С' на угол ВАС (рис.4.5) и установим углы поворота отрезков относительно своих первоначальных положений – α1 и α2. Величина α1 + α2 = γmn и есть деформация сдвига в точке А в плоскости mn.
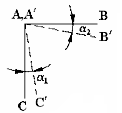 Положительными принимают линейную деформа-цию, соответствующую растяжению, и деформацию сдвига, отвечающую уменьшению первоначального угла пересечения отрезков.
Положительными принимают линейную деформа-цию, соответствующую растяжению, и деформацию сдвига, отвечающую уменьшению первоначального угла пересечения отрезков.
Полагая деформации малыми, мы можем в дальнейшем пренебрегать ими по сравнению с едини-цей, а также их высокими степенями по сравнению с первой степенью.
Рис. 4.5 Деформированное состояние в точке – состояние тела в окрестности данной точки, определяемое совокупностью деформаций всех линейных элементов, проходящих через данную точку. В случае малых деформаций оно полностью определяется линейными деформациями трех взаимно перпендикулярных линейных элементов тела, проходящих через данную точку, и тремя деформациями сдвига этих линейных элементов. Соответствующие шесть независимых скалярных величин определяют тензор деформаций:
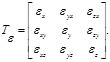
 |
Здесь
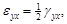
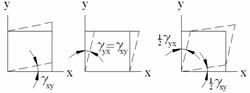
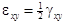 (при γyx=γxy),…Последнее оправдывается идентичностью трех ситуаций для грани деформированного параллелепипе-да, что видно, например, из рис. 4.6 (в плоскости xy).
(при γyx=γxy),…Последнее оправдывается идентичностью трех ситуаций для грани деформированного параллелепипе-да, что видно, например, из рис. 4.6 (в плоскости xy).
Рис. 4.6
Главные оси деформации – три взаимно перпендикулярные прямые, прохо-дящие через данную точку тела и совпадающие по направлениям с такими тре-мялинейными элементами тела, которые остаются взаимно перпендикулярны-ми и после деформации. Линейные деформации по направлениям этих осей на-
зываются главными деформациями и обозначаются ε1, ε2, ε3 (ε1 ≥ ε2 ≥ ε3).
Кинематические граничные условия на части поверхности тела с заданным вектором перемещений 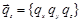 имеют вид
имеют вид 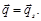
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|