Практикум. Примеры

4.4 Практикум

Примеры

1. По двум взаимно перпендикулярным площадкам действуют только касатель-ные напряжения τ (чистый сдвиг). Определить положение главных площадок и величины главных напряжений.

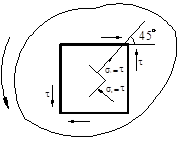Решение: σ_гл.=0± 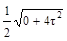= ± = ± 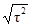τ.

Поскольку между главными напряжениями существу-ет соотношение σ₁ 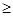σ₂ 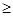σ₃, то расположив значения главных напряжений на числовой оси, установим:

σ₁>τ; σ₂>τ; σ₃>-τ;

tg2α_о= 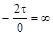; 2α_оarctg = 90 ; α_о=45

Повернув, на α_о= - 45 площадки по отношению к исходным получаем “глав-ные”. σ₁> 0, поэтому вектор растягивающего напряжения ориентируем от сечения , а вектор сжимающего σ₃к сечению. Знак минус таким образом реализован направлением вектора.

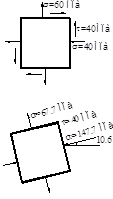2. Определить величину и направление главных напряжений для случая плоского напряжённого состояния, показанного на рисунке:

Решение. Следует помнить, что в формулах:

σ_гл.= 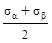± 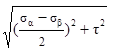и tg2α_о= -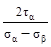

1) σ_α > σ_β алгебраически,

2) Знак τ_α определяется на площадке, где действует большее нормальное напряжение (σ_α), а учитывая, что Q= 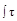dx знак τ > 0 будет в случае,

если поперечные силы Q > 0, т.е. стремятся повернуть площадку “по часовой стрелке”,

3) если α_о> 0, то поворот совершают “против часовой стрелки” от вектора σ_α> 0, с учётом сказанного: σ_α= + 60 МПа; σ_β= -140 МПа; τ_α= - 40 МПа.

σ_гл.= 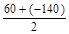± 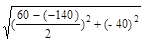= - 40 ± 107.7.

σ₁= + 67.7 МПа; σ₂=0; σ₃= -147.7 МПа (касательные напряжения в главных площадках отсутствуют).

tg2α_о= 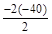= = 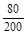0.4; 2α_о= arctg0.4 = 21.2

α_о=10.6 (поворот против часовой стрелки).

⇐ Предыдущая 10 11 12 13 141516 17 18 19 Следующая ⇒