Главная

Контакты

Случайная статья

• Автоматизация
• Антропология
• Археология
• Архитектура
• Биология
• Ботаника
• Бухгалтерия
• Военная наука
• Генетика
• География
• Геология
• Демография
• Деревообработка
• Журналистика
• Зоология
• Изобретательство
• Информатика
• Искусство
• История
• Кинематография
• Компьютеризация
• Косметика
• Кулинария
• Культура
• Лексикология
• Лингвистика
• Литература
• Логика
• Маркетинг
• Математика
• Материаловедение
• Медицина
• Менеджмент
• Металлургия
• Метрология
• Механика
• Музыка
• Науковедение
• Образование
• Охрана Труда
• Педагогика
• Полиграфия
• Политология
• Право
• Предпринимательство
• Приборостроение
• Программирование
• Производство
• Промышленность
• Психология
• Радиосвязь
• Религия
• Риторика
• Социология
• Спорт
• Стандартизация
• Статистика
• Строительство
• Технологии
• Торговля
• Транспорт
• Фармакология
• Физика
• Физиология
• Философия
• Финансы
• Химия
• Хозяйство
• Черчение
• Экология
• Экономика
• Электроника
• Электротехника
• Энергетика

Контрольные тесты. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ. СЕЧЕНИЙ. Основные понятия

Контрольные тесты

1. Построить эпюры Q, M и определить Q_мax, M_мax.

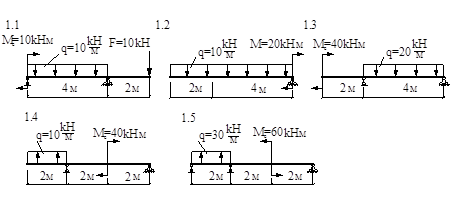
(1.1) Q_мax [кH]: (а) 10; (б)35  (в)40; (г)55.

        M_мax [кHм] (д) 40; (е) 41.5; (ж)20; (з) 37.5.

(1.2) Q_мax [кH]: (а) 20; (б)30; (в)40; (г)50.

        M_мax [кHм] (д) 20; (е) 30; (ж)40; (з) 50.

(1.3) Q_мax [кH]: (а) 20; (б)35; (в)45; (г)50.

        M_мax [кHм] (д) 52.5; (е) 63.5; (ж)40; (з) 42.5.

(1.4) Q_мax [кH]: (а) 15; (б)20;   (в)25; (г)40.

        M_мax [кHм] (д) 10; (е) 20; (ж)30; (з) 40.

(1.5) Q_мax [кH]: (а) 20; (б)30; (в)40; (г)60.

        M_мax [kH м] (д) 20; (е) 30; (ж)40; (з) 60.

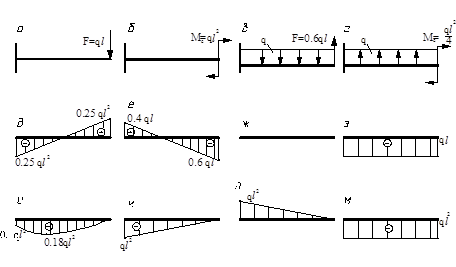2. Для расчётных схем а, б, в, г найдите соответствующие эпюры (д, е, ж, з) поперечных сил и эпюры (и, к, л, м) изгибающих моментов (длина балки – l).

3. Для расчётных схем а, б, в, г найдите соответствующие эпюры (д, е, ж, з) поперечных сил и эпюры (и, к, л, м) изгибающих моментов (длина каждого участка – l, М_е=ql²).

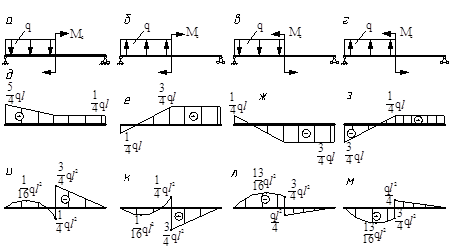
4. Построить эпюры изгибающих моментов и определить М_мах:

[4.1] (а) 30; (б) 35; (в) 40; (г) 45.               [4.4] (а) 30; (б) 35; (в) 40; (г) 45.

[4.2] (а) 70; (б) 76.25; (в) 78.25; (г) 90.25. [4.5] (а) 12.5; (б) 20; (в) 25; (г) 30.

[4.3] (а) 15; (б) 30; (в) 45; (г) 60.

3. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ

 СЕЧЕНИЙ

3.1. Основные понятия

Основным объектом, изучаемым в курсе, является стержень. Сопротивление стержня различным видам деформирования часто зависит не только от его материала и размеров, но и от характера осевой линии, формы поперечных сечений и их ориентации.

Уже в древности строители знали, что доска или брус, поставленные на ребро, во много раз лучше противостоят изгибу, чем положенные плашмя. Речь идет как об их несущей способности, так и о деформативности. Для двутавровой стандартной балки, поставленной на две опоры, эти показатели примерно в 7 и 30 раз выше, чем у балки квадратного поперечного сечения такой же площади, cделанной из того же материала. Таким образом, рациональное расположение материала по сечению позволяет снизить его расход.

Как увидим дальше, этот вывод имеет обобщение на форму конструкции в целом. Но в данный момент, отвлекаясь от физических свойств изучаемого объекта, рассмотрим основные геометрические характеристики поперечных сечений стержня, определяющие сопротивление различным видам его деформирования.

Рассмотрим плоскую фигуру (рис.3.1), связанную с системой координат z0y. Выделяя элемент площади dA, составим выражения:

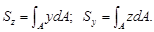
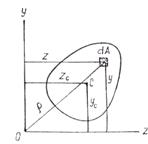(Интегрирование проводится по площади сечения А.)

Эти геометрические характеристики называются статическими моментами площади сечения относительно осей 0z и 0у. Их размерность – м³. Статический момент может быть положительным, отрицательным и равным нулю. В последнем случае ось проходит через центр тяжести фигуры и называется центральной. Из теоретической меха-

 ники известны координаты центра тяжести С

                Рис. 3.1          (рис.3.1):

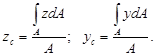
Эти выражения позволяют определить положение центра тяжести, если найдены статические моменты, или, наоборот, найти статические моменты, если известно положение центра тяжести:

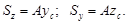
Если сложную фигуру можно разбить на n простых частей, для каждой из которых известна площадь A_i и координаты центра тяжести z_ci и y_ci, то статический момент площади всей фигуры относительно данной оси определяется как сумма статических моментов каждой части:

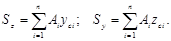
В дальнейшем мы будем использовать геометрические характеристики, при вычислении которых элементарная площадь dA умножается на квадрат расстояния до оси:

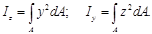
Они называются осевыми моментами инерции сечения, а их размерность – м⁴.

Им соответствуют радиусы инерции:

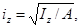
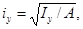
по которым строится эллипс инерции.

Интеграл с той же размерностью

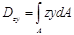
называется центробежным моментом инерции сечения. В отличие от осевого момента инерции, который всегда положителен, он может быть положительным, отрицательным и равным нулю. Последний случай заслуживает особого рассмотрения, которое последует ниже.

Еще одна характеристика, называемая полярным моментом инерции сечения, представляет собой интеграл произведений элементарных площадей на квадраты их расстояний от полюса (см. рис.3.1):

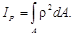
В случае совпадения начала координат и полюса полярный момент инерции равен сумме двух осевых моментов инерции:

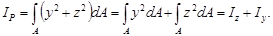
Если через точку О проходят две системы координат –zОу и z₁Oy₁, то справедливо равенство

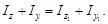
Оно следует из того, что каждая из указанных сумм в отдельности равна полярному моменту инерции относительно точки 0.

Поскольку интеграл по площади равен сумме интегралов, взятых по n отдельным частям, составляющим эту площадь, то для сложной фигуры применимы равенства:

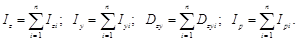
Для прокатных профилей (двутавра, швеллера, уголка и т.п.) моменты инерции приводятся в таблицах сортамента.