
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
h = ha+hf=m+1,25m=2,25m.. c=hf-ha=0,25m.. da=d+2ha=z·m+2m=m(z-2).. df=d-2hf=z·m-2m=m(z-2). s=sв=p/2=π·m/2=1,57m.. aw=r1+r2=z1·m/2+z2·m/2=m(z1+z2)/2.
ha=m
Высота ножки зуба принимается равной 1,25 модуля
hf= 1,25m
Высота зуба
h = ha+hf=m+1,25m=2,25m.
Разница в высоте ножки зуба одного колеса и высоте головки зуба другого необходима для образования радиального зазора
c=hf-ha=0,25m.
Диаметр окружности выступов
da=d+2ha=z·m+2m=m(z-2).
Диаметр окружности впадин
df=d-2hf=z·m-2m=m(z-2)
Модуль зацепления, можно определить, зная диаметр окружности выступов
m=da/(z+2).
Теоретическая толщина зуба s и ширина впадины sв по делительной окружности равны между собой
s=sв=p/2=π·m/2=1,57m.
Однако, чтобы создать боковой зазор, необходимый для нормальной работы зубчатой пары, зуб делается несколько тоньше, вследствие чего он входит во впадину свободно.
Межцентровое (межосевое) расстояние двух сцепляющихся зубчатых колес определяется по формуле
aw=r1+r2=z1·m/2+z2·m/2=m(z1+z2)/2.
 Дугой зацепления называют путь, проходимый профилем зуба по начальной окружности за время фактического его зацепления. Дуга зацепления обозначается буквой S.
Дугой зацепления называют путь, проходимый профилем зуба по начальной окружности за время фактического его зацепления. Дуга зацепления обозначается буквой S.
Необходимым условием непрерывности зацепления является требование, чтобы дуга зацепления была больше шага зацепления, т.е. чтобы S >р.
Отношение длины дуги зацепления к шагу зацепления называется коэффициентом перекрытия
ε=s/p.
Коэффициент перекрытия характеризует среднее число пар зубьев, одновременно находящихся в зацеплении. Для цилиндри-ческих зубчатых передач принимают ε≥1,2.
2 Практическая часть.
Определяем геометрические размеры зубчатого колеса
-ширина - 100 мм.;
-диаметр окружности выступов — 130 мм.;
-диаметр окружности впадин — 105 мм.;
-число зубьев — 11;
-диаметр отверстия под вал - 42 мм.;
-шпоночный паз - 6x4 мм.
3 Расчётная часть
3.1 Определяем модуль зубчатого колеса
m=(da-df)/2,5;
m=(130-105)/2,5=25/2,5=10 мм;
3.2Определяем диаметр начальной окружности
d=m·z1
d=10·11=110 мм
Билет 13




3 Материалы зубчатых колес.
Основными материалами зубчатых колес служат термически обрабатываемые стали, так как они по сравнению с другими материалами в наибольшей степени обеспечивают контактную прочность и прочность зубьев на изгиб. Реже зубчатые колеса выполняют из чугунов и пластмасс.
В зависимости от твердости рабочих поверхностей стальных зубьев различают зубчатые колеса твердостью НВ≤350, нормализованные, улучшенные или закаленные, и зубчатые колеса твердостью НВ>350, закаленные, цементированные, азотированные и цианированные. Чистовое нарезание зубьев стальных зубчатых колес твердостью НВ≤350 производят после окончательной термообработки. При этом получают довольно высокую точность изготовления зубьев без применения дорогих отделочных операций (шлифовки, притирки и т. п.). Стальные зубья твердостью НВ≤350 хорошо прирабатываются и не подвержены хрупкому разрушению при динамических нагрузках. Для лучшей прирабатываемости твердость зубьев шестерни рекомендуется принимать больше твердости зубьев колеса. Благодаря технологическим преимуществам стальные зубчатые колеса твердостью НВ≤350 имеют широкое применение в мало- и средненагруженных передачах, а также в передачах с большими колесами, термическая обработка которых затруднена.
Улучшенные зубчатые колеса изготовляют обычно из качественных углеродистых сталей 35, 40, 45, 50, 50Г и легированных сталей 35Х, 40Х, 40ХН и др. Нормализованные зубчатые колеса небольших размеров выполняют из углеродистой стали обыкновенного качества Ст5, Ст6 и качественных углеродистых сталей 35, 40, 45 и 50, а больших размеров - из углеродистого стального литья 35Л, 40Л, 45Л, 50Л, а также из марганцовистого н низколегированного стального литья различных марок.
Для повышения контактной прочности зубьев и соответственно нагрузочной способности зубчатых передач применяют стальные зубчатые колеса твердостью НВ>350. С увеличением твердости рабочей поверхности зубьев возрастают также износостойкость и сопротивление заеданию зубьев. Однако зубья с большой твердостью рабочей поверхности плохо прирабатываются и нуждаются в высокой точности изготовления. Кроме того, их механическая обработка затруднена, для облегчения ее эти зубья нарезают до термической обработки. Так как некоторые виды термообработки вызывают коробление зубьев, то для исправления формы зубьев применяют отделочные операции: шлифовку, притирку, обкатку и т. п.
Закалка зубьев.
Закалка зубьев может быть объемной, осуществляемой в воде или масле, и поверхностной, осуществляемой для зубчатых колес малых и средних размеров токами высокой частоты (ТВЧ), а для крупных зубчатых колес — с нагревом ацетиленовым пламенем. Недостатками объемной закалки являются повышение коробления зубьев и понижение вязкости их сердцевины, вызывающее уменьшение прочности зубьев на изгиб при действии ударных нагрузок. Поэтому объемная закалка во многих случаях заменяется поверхностной закалкой, цементацией, азотированием и цианированием.
Зубчатые колеса из чугуна.
Чугуны применяют для изготовления крупногабаритных зубчатых колес тихоходных и в особенности открытых передач, где они могут работать при бедной смазке, так как чугунные зубья сравнительно хорошо сопротивляются заеданию. Основной недостаток обычных серых чугунов — их пониженная прочность, особенно при ударных нагрузках. Но чугунные зубья сравнительно хорошо сопротивляются выкрашиванию, чугунные зубчатые колеса легче отливать, и они значительно дешевле зубчатых колес из стального литья. Поэтому высокопрочные чугуны широко применяют вместо стального литья для изготовления зубчатых колес закрытых передач. Чугунные зубчатые колеса изготовляют из серого чугуна СЧ21, СЧ24, модифицированного чугуна СЧ25, СЧ30, СЧ35, а также из высокопрочного чугуна всех стандартных марок. Для неответственных зубчатых колес применяют серый чугун СЧ15 и СЧ18.
Зубчатые колеса из пластмассы.
Пластмассы применяют в быстроходных малонагруженных передачах. Пластмассовые зубчатые колеса изготовляют главным образом из древеснослоистых пластиков (ДСП), текстолита и полиамидов (нейлона и капрона).
Достоинства пластмассовых зубчатых колес по сравнению с металлическими зубчатыми колесами — это способность амортизировать удары при передаче переменных нагрузок и гасить механические вибрации и тем самым обеспечивать бесшумность работы передачи; более низкий износ зубьев.
Шестерни из текстолита и ДСП.
Шестерни из текстолита и ДСП применяют обычно в паре с металлическими колесами в тех случаях, когда требуется уменьшить динамические нагрузки и шум, а также когда трудно или невозможно добиться точного выполнения или установки деталей передачи. Такие зубчатые колеса широко применяют в передачах небольшой мощности от электродвигателей к различным станкам и в других установках, подшипники валов которых располагаются в отдельных корпусах. Чтобы не повредить зубья пластмассовой шестерни кромками зубьев металлического колеса, ширина колеса должна быть больше ширины сопрягаемой пластмассовой шестерни.
Зубчатые колеса из полиамидов.
Зубчатые колеса из полиамидов широко применяют в приборах и небольших силовых установках. Износ полиамидных зубьев незначительный, и полиамидные зубчатые колеса могут работать без смазки. Так как полиамиды химически устойчивы, то полиамидные зубчатые колеса применяют при работе в агрессивной среде, например в шестеренчатых насосах для перекачки химически активных жидкостей.
В некоторых случаях, когда рабочие поверхности зубьев металлических зубчатых колес подвергаются сильному износу, их покрывают тонким слоем (0,05...0,5 мм) нейлона. Покрытие осуществляется погружением зубьев, нагретых до температуры плавления нейлона, в порошкообразный нейлон. При этом на поверхности металлических зубьев образуется ровный, тонкий и прочно соединенный с металлом слой нейлона, не требующий какой-либо последующей обработки. В этом случае комбинируют антифрикционные и износостойкие свойства нейлонового покрытия зубьев с высокой прочностью на изгиб металлических зубчатых колес.
Билет 14

КРУЧЕНИЕ
Вид деформации при котором возникает один внутренний силовой фактор-крутящий момент, называется кручением.

c1
b c

 d1
d1

 a d Mвр
a d Mвр
γ-угол сдвига
Вал- стержень, работающий на кручение












 τ τ
τ τ
 -Закон парности касательных напряжений
-Закон парности касательных напряжений

τ
 τ Деформация чистого сдвига рассматривается на примере кручения тонкостенной трубы. При чистом сдвиге возникают только касательные напряжения.
τ Деформация чистого сдвига рассматривается на примере кручения тонкостенной трубы. При чистом сдвиге возникают только касательные напряжения.
Закон Гука при кручении
В пределах упругих деформаций возникают касательные напряжения, которые прямопропорциональны углу сдвига.
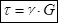
G-модуль сдвига
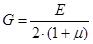 ; для стали Ст3 - G=8∙104МПа
; для стали Ст3 - G=8∙104МПа
Эпюра крутящих моментов- диаграмма крутящих моментов по длине вала.







 I M1 II M2 III M2 IV M4 V M1=60кНм
I M1 II M2 III M2 IV M4 V M1=60кНм
М2=20кНм
М3=35кНм
М4= 5кНм

I II III IV V 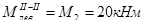
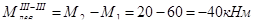

20 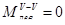

-5 Мкр
-40
Крутящий момент в сечении численно равен алгебраической сумме всех внешних сил расположенных в плоскости ┴оси вала относительно точки центра тяжести сечения и находящийся по одну сторону от рассматриваемого сечения.
Правило знаков
Крутящий момент в сечении а-а считается положительным, когда внешний момент вращаем отсеченную часть против часовой стрелки, если смотреть на отсеченную часть со стороны сечения. Если же внешний момент вращает отсеченную часть по часовой стрелке (при взгляде со стороны сечения), то крутящий момент в сечении будем считать отрицательным.
 |  |  |  | ||||||
 | |||||||||
М М М М
● ┼ ┼ ●
Мкр>0 Мкр<0
 а а
а а
 |  |  |  |  |
а а



 ┼ ● ● ┼
┼ ● ● ┼
 |  |

 Мкр ┼ ▬ Мкр
Мкр ┼ ▬ Мкр
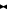

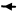
















 Условия прочности и жесткости при кручении
Условия прочности и жесткости при кручении

I II

 r
r
 N1 C1 δ
N1 C1 δ

 O O1
O O1
 φ Mвр
φ Mвр
 K γ N C
K γ N C
 L
L
Угол сдвига для элемента, лежащего на поверхности стержня, равен отношению отрезка NN1 к длине элемента dz
 (1)
(1)
Выделяя мысленно из рассматриваемой части бруса цилиндр произвольного радиуса δ и повторяя те же рассуждения, получим угол сдвига для элемента, отстоящего на расстоянии δ от оси стержня
 (2)
(2)
На основании закона Гука при сдвиге имеем

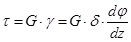 (3)
(3)
Как видим, при кручении деформации сдвига и касательные напряжения прямо пропорциональны расстоянию от центра тяжести сечения.
Эпюра касательных напряжений




























 τ max
τ max
D
 D1
D1
φ r δ τ
C1 C
B1 B
В центре тяжести касательные напряжения равны нулю. Наибольшие касательные напряжения будут в точках сечения, расположенных у поверхности сечения.
Равнодействующий момент касательных напряжений в сечении:
 (4)
(4)
где  -элементарный крутящий момент внутренних сил, действующих по площадке dA.
-элементарный крутящий момент внутренних сил, действующих по площадке dA.
Подставив в (4) значение напряжений из формулы (3), получим
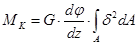 (5)
(5)
Имея в виду, что
 , (6)
, (6)
Где  - полярный момент инерции сечения, получим
- полярный момент инерции сечения, получим

 (7)
(7)
Подставляя значение  в формулу (3), имеем
в формулу (3), имеем
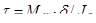 (8)
(8)
В частном случае, когда на стержень действует один внешний скручивающий момент М, из условия равновесия отсеченной части стержня получим МК=М.
Таким образом, окончательная формула для определения касательных напряжений при кручении имеет вид
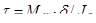 (9)
(9)
Эта формула показывает, что, в точках, одинаково удаленных от центра сечения, напряжения τ одинаковы. Наибольшие напряжения в точках у контура сечения равных
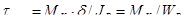 , (10)
, (10)
Где
 (11)
(11)


Билет 15








2Эпюра крутящих моментов- диаграмма крутящих моментов по длине вала.

 I M1 II M2 III M2 IV M4 V M1=60кНм
I M1 II M2 III M2 IV M4 V M1=60кНм
М2=20кНм
М3=35кНм
М4= 5кНм
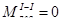
I II III IV V 
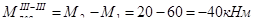
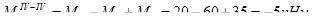
20 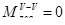

-5 Мкр
-40
Крутящий момент в сечении численно равен алгебраической сумме всех внешних сил расположенных в плоскости ┴оси вала относительно точки центра тяжести сечения и находящийся по одну сторону от рассматриваемого сечения.
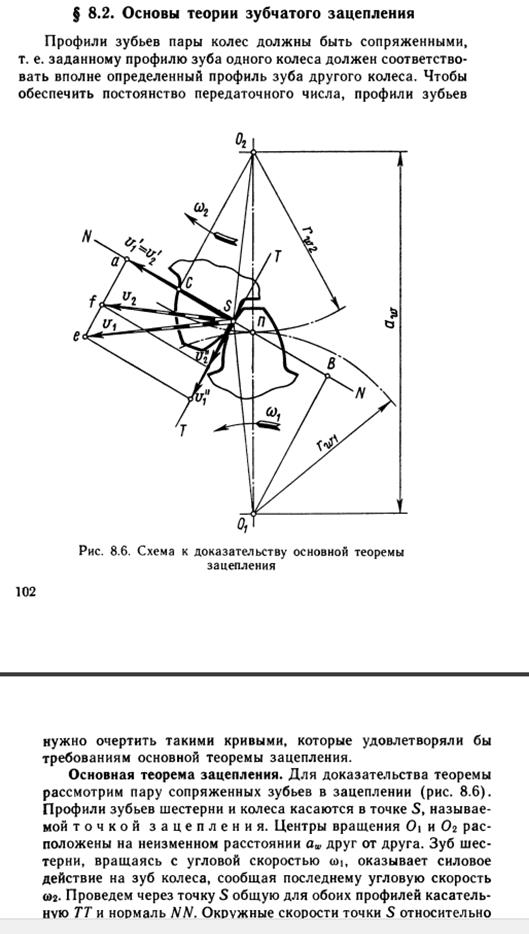
Правило знаков
Крутящий момент в сечении а-а считается положительным, когда внешний момент вращаем отсеченную часть против часовой стрелки, если смотреть на отсеченную часть со стороны сечения. Если же внешний момент вращает отсеченную часть по часовой стрелке (при взгляде со стороны сечения), то крутящий момент в сечении будем считать отрицательным.
М М М М
 ● ┼ ┼ ●
● ┼ ┼ ●
Мкр>0 Мкр<0
а а
а а
┼ ● ● ┼
Мкр ┼ ▬ Мкр
3

|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|