
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Проверка прочности.. Проектный расчет.. Определение максимально допустимой нагрузки.. Проверка прочности.. Проектный расчет.. Определение максимально допустимой нагрузки.
1. Проверка прочности.
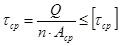
2. Проектный расчет.
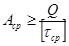
3. Определение максимально допустимой нагрузки.
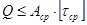
При решении задач на срез болтов, штифтов, заклепок принимается
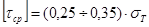 или
или 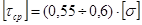
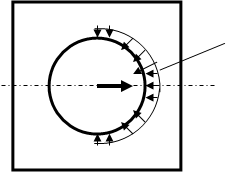
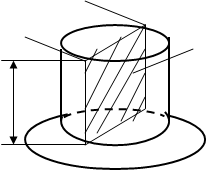
 Смятие- местная деформация сжатия по площади передачи давления, в результате чего возникают нормальные напряжения, которые быстро ослабевают при удалении от площадок передачи давления.
Смятие- местная деформация сжатия по площади передачи давления, в результате чего возникают нормальные напряжения, которые быстро ослабевают при удалении от площадок передачи давления.
 d
d
` 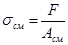 Асм
Асм
F
 Δ
Δ
Условия прочности при смятии 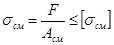
Допущения
Считаем, что нормальные напряжения распределены по всей площади контакта равномерно и перпендикулярно к площади контакта

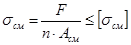
n- число соединительных элементов
Асм – площадь смятия
[σсм]- допускаемое напряжение смятия.
На смятие решаются 3 вида задач:
1. Проверка прочности.
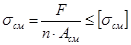
2. Проектный расчет.
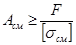
3. Определение максимально допустимой нагрузки.
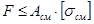
При небольшой толщине соединяемых пластин и значительных нагрузках между поверхностью соединительных деталей и стенками отверстий возникает взаимное давление, в результате стенки отверстий обминаются.
Давление, возникающее между поверхностью соединительных деталей и отверстием – напряжение смятия σсм.



Билет 12
1 




3Соприкасающиеся друг с другом окружности на ведущем и ведомом
колесах, которые имеют общие оси с зубчатыми колесами и катятся друг по другу без скольжения, называются начальными.

Диаметры начальных окружностей обозначаются dwi и dw2. Окружность, на которой расстояние между одноименными сторонами двух 'соседних зубьев равно шагу зуборезного инструмента, называется делительной, ее диаметр обозначается d. Делительные окружности совпадают с начальными,
если межцентровое расстояние пары зубчатых колес равно сумме радиусов делительных окружностей. У данного колеса существует только одна делительная окружность; она выбирается в качестве базы для
определения основных размеров зубчатого колеса.
Окружной шаг зубчатого зацепления p – есть расстояние между
 одноименными сторонами двух соседних зубьев колеса, измеренное по дуге делительной окружности.
одноименными сторонами двух соседних зубьев колеса, измеренное по дуге делительной окружности.
Из определения шага следует, что длина делительной окружности равна πd = pz. Отсюда диаметр делительной окружности
d=p·z/π,
Частное от деления p/π называется модулем зубьев и обозначается буквой т
р/п=т,
Подставив значение модуля в формулу
d=m·z1
откуда
m=d/z.
Таким образом, модуль зубьев т можно определить как часть диаметра делительной окружности, приходящуюся на один зуб колеса. Поэтому модуль называется иногда диаметральным шагом.
Для унификации зуборезного инструмента и взаимозаменяемости зубчатых колес значение модулей зубьев следует выбирать по стандарту СТ СЭВ 310—76. Этим стандартом дан ряд значений от 0,05 до 100 мм. Приводим значение модулей зубьев от I до 25 мм:
1-й ряд (предпочтительный): 1; 1,25; 1,5; 2,0; 2Э5; 3,0; 4э0; 5,0; 6,0; 8,0; 10,0; 12,0; 16,0; 20,0; 25,0;
2-й ряд: 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14; 18; 22.
Окружность 1, описанная из центра колеса и ограничивающая вершины его головок, называется окружностью вершин.
Окружность 2, описанная из центра колеса и ограничивающая его впадины со стороны тела колеса, называется окружностью впадин.
 Высотой зуба h называется радиальное расстояние между окружностью выступов и окружностью впадин.
Высотой зуба h называется радиальное расстояние между окружностью выступов и окружностью впадин.
Согласно ГОСТ -13755—68 высота головки зуба принимается равной модулю
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|