Лемма о параллельном переносе силы

§ 5.1. Лемма о параллельном переносе силы

Лемма. Механическое состояние твердого тела не нарушится, если данную силу перенести параллельно самой себе в произвольную точку тела, добавив при этом пару, момент которой равен моменту данной силы относительно новой точки приложения.

Возьмем тело, находящееся под действием некоторой системы сил, в числе которых есть сила Р, приложенная в точке

А (рис. 5.1). Выберем произвольную точку О, которую назовем центром приведения, и на основании аксиомы IV приложим в этой точке две равные силы F' и F", параллельные данной силе F, причем

F'= F"=F.

Систему сил (F, F', F"), эквивалентную силе F, представим как силу F, перенесенную параллельно самой себе в произвольно выбранный центр приведения О, и пару (F, F"), момент которой равен моменту данной силы относительно центра приведения О, являющегося новой точкой приложения силы:

М(F,F")=Fа=М₀(F).

Лемма доказана.

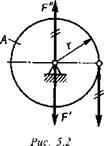
Описанный выше перенос силы можно показать на примере. Рассмотрим колесо А радиуса r , вращающееся на оси в подшипниках (рис. 5.2). Пусть к ободу колеса по касательной приложена сила F (такую силу называют окружной).

Для определения действия силы F на колесо и подшипники применим доказанную лемму и перенесем эту силу параллельно самой себе на ось колеса. В результате получим силу F' =F, вызывающую давление на подшипники, и пару сил (F, F") с моментом, равным Fr, которая будет вращать колесо.

2 МЕТОД СЕЧЕНИЙ

В.С.Ф.- внутренние силовые факторы – силы, которые внутри и препятствуют изменению формы и размера.

Y N=∑F_nZ; M_K=∑M_Z(F_K) Условия

M_иQ_Y=∑F_nY; M_и_X=∑M_X(F_n) равновесия

Q_YQ_X=∑F_nX; M_и_Y=∑M_Y(F_n)

N-продольная сила

Q_X, Q_Y –поперечные

Q_X X M_K- крутящий момент

N_ZM_иХ, М_иУ – изгибающие моменты

M_кр

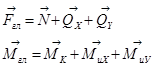
Вид деформации зависит от наличия внутренних силовых факторов

N-растяжение или сжатие;

M_к- кручение;

M_иХили М_иУ – чистый изгиб;

М_иХ+Q_Y или М_иУ+Q_X – прямой поперечный изгиб;

Q_X или Q_Y – сдвиг;

М_иХ и М_иУ – косой изгиб.

Для выявления внутренних сил в сопротивлении материалов применяется метод сечений. Метод сечений позволяет определить внутренние силовые факторы и виды нагрузок.

3 ВИНТОВЫЕ МЕХАНИЗМЫ

Общие сведения.

Кинематические и силовые соотношения

Передача винт—гайка предназначена для преобразования вращательного движения одного из элементов пары в поступательное перемещение другого. При этом как винт, так и гайка могут иметь либо одно из названных движений, либо оба движения вместе.

К достоинствам винтовых механизмов относятся: простота получения медленного поступательного движения и возможность большого выигрыша в силе, плавность, бесшумность, способность воспринимать большие нагрузки, возможность осуществления перемещений с высокой точностью, простота конструкций.

Недостатками винтовых механизмов являются: большие потери на трение и, как следствие, низкий КПД.

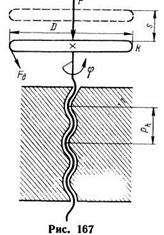
Винты в винтовых механизмах в зависимости от назначения разделяют на грузовые (домкраты, прессы) и ходовые (служащие для точной передачи движения в станках, измерительных устройствах). Определим кинематические соотношения в винтовой паре. На рис. 167 показана схема винтового механизма. Винт вращается вокруг продольной оси и перемещается вдоль нее. Поступательное перемещение винта 5 определяется ходом резьбы р_ь и углом поворота <р

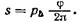
Скорость поступательного движения

и угловая скорость вращения винта равны производным от соответствующих перемещений по времени.

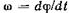
Отсюда находим

⇐ Предыдущая 1 234 5 6 7 8 Следующая ⇒