
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
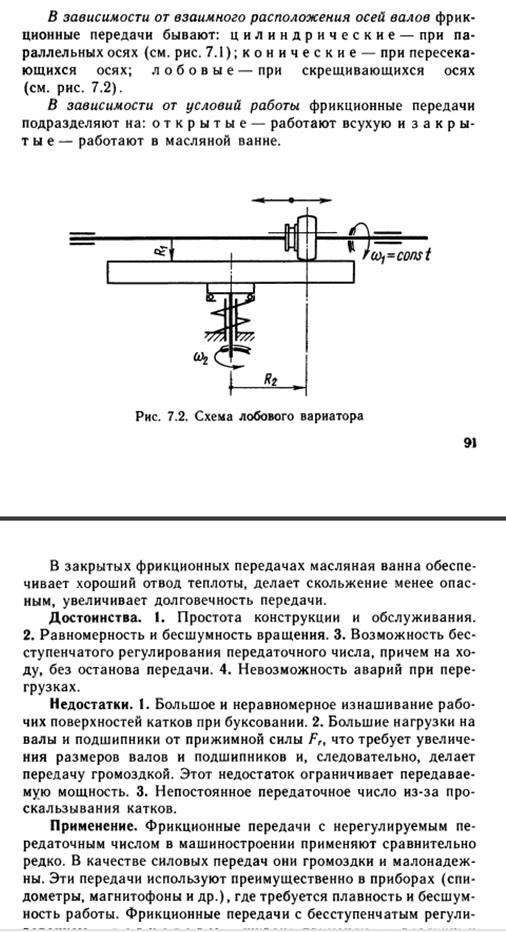
Проекция силы на ось в пространстве
§ 7.2. Проекция силы на ось в пространстве
Определение проекции силы на ось остается прежним (см. § 2.3). Если сила и ось не лежат в одной плоскости, то проецирующие перпендикуляры также не лежат в одной плоскости (рис. 7.1).
Для того чтобы определить, чему равна проекция силы F на ось Ох, следует мысленно провести через начало или конец силы ось 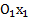 , параллельную данной оси Ох, тогда Fх = Fсоs α , так как FХ =
, параллельную данной оси Ох, тогда Fх = Fсоs α , так как FХ = 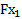
Правило знаков для проекций остается прежним.
Если вектор силы параллелен оси, то он проецируется на эту ось в натуральную величину.
Если вектор силы лежит в плоскости, перпендикулярной оси, то его проекция на эту ось равна нулю.
2 ПОСТРОЕНИЕ ЭПЮР ПРОДОЛЬНЫХ СИЛ И НОРМАЛЬНЫХ НАПРЯЖЕНИЙ
Эпюры продольных сил – называется диаграмма изменения продольных сил по длине стержня.
Эпюры нормальных напряжений – это диаграмма изменения нормальных напряжений по длине стержня.
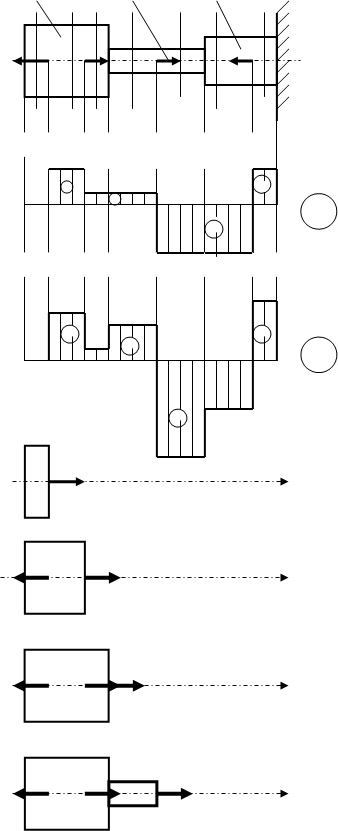 А1=5см2 А2=2см2 А3=4см2
А1=5см2 А2=2см2 А3=4см2
I II III IV V VI VII F1=15кН
F2=10кН
F1 F2 F3 F4 F3=20кН
F4=35кН
I II III IV V VI VII
ЭПЮРА ПРОДОЛЬНЫХ СИЛ
15 15
+ 5 +
N
-15 -
ЭПЮРА НОРМАЛЬНЫХ НАПРЯЖЕНИЙ
31 50
11 25
0 σ
37,5
75







 I N1 Z ∑FnZ=0
I N1 Z ∑FnZ=0
∑FnZ=N1=0
I
II
F1 N2 ∑FnZ=0
Z ∑FnZ=N2-F1=0
N2=F1=15кН
II
III ∑FnZ=0
F1 F2 N3 ∑FnZ=N3-F1+F2=0
Z N3=F1-F2=15-10=5кН
III
IV
F1 F2 N4
Z N4=N3=5кН
V
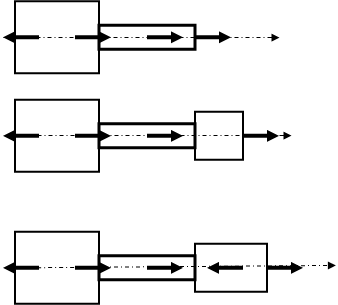 F1 F2 F3 ∑FnZ=0
F1 F2 F3 ∑FnZ=0
N5 Z ∑FnZ=N5-F1+F2+F3=0
N5=F1-F2-F3=15-10-20=-15кН
VI
F1 F2 F3 N6
Z N6=N5=-15кН
VI
VII
N7 ∑FnZ=0
F2 F3 F4 FnZ=N7-F1+F2+F3-F4=0
N7
F1 VII Z N7=F4+F1-F3-F2=20кН
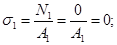
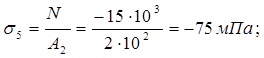
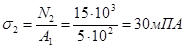 ;
; 
 ;
; 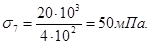


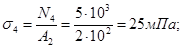
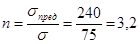

Билет 10
|
|
| 2 |
|
|

Билет 11
|
|
|
|
2 СРЕЗ СМЯТИЕ
Срезом называется деформация, которая возникает под действием 2Х близко расположенных параллельно и противоположно направленных сил. При этом возникают касательные напряжения.
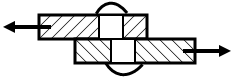 |
Р
Р
Допущения
1. В поперечных сечениях детали возникает один силовой фактор- поперечная сила Q.
2. Касательные напряжения распределяются по сечению равномерно.

3. Если соединение выполнено с помощью нескольких одинаковых элементов, то каждый из этих элементов испытывает одинаковую нагрузку.
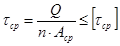 , где n-количество заклепок (болтов)
, где n-количество заклепок (болтов)
На срез решаются 3 вида задач:
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|




