я – проектный расчет. я – определение максимально допускаемой нагрузки. Глава 7 ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ. Пространственная система сходящихся сил

2-я – проектный расчет

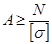
3-я – определение максимально допускаемой нагрузки

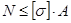
3 ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К МАШИНАМ И МЕХАНИЗМАМ

малая масса и минимальные габариты — деталь должна иметь достаточные прочность, жесткость и износостойкость при минимально возможных габаритах и массе;

недефицитность материалов — удовлетворение всех предыдущих требований не должно осуществляться за счет применения дефицитных материалов, так как использование таких материалов приводит к резкому увеличению стоимости детали;

технологичность — форму и материал детали желательно выбирать такими, чтобы изготовление ее требовало наименьших затрат труда и времени и энергоемкости;

безопасность — форма и размеры детали должны обеспечивать безопасность обслуживающего персонала при изготовлении и эксплуатации машины;

простота в обслуживании и эксплуатации;

соответствие государственным стандартам — деталь должна удовлетворять действующим стандартам на формы, размеры, сорта и марки материала.

Билет 9

Глава 7 ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ

§ 7.1. Пространственная система сходящихся сил

Система сил, линии действия которых расположены в различных плоскостях, называется пространственной системой сил.

Пространственная система сил называется сходящейся, если линии действия всех сил системы пересекаются в одной точке.

Теорема. Пространственная система сходящихся сил эквивалентна равнодействующей, которая равна векторной сумме этих сил; линия действия равнодействующей проходит через точку пересечения линий действия составляющих сил.

Пусть дана пространственная система п сходящихся сил (F_1, F₂, F₃. ..., 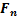). На основании следствия из аксиом III и IV перенесем все силы системы вдоль линий действия в точку их пересечения. Затем на основании аксиомы параллелограмма сложим силы F₁ и F₂ , в результате чего получим их равнодействующую:

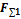= F₁₊ F₂ .

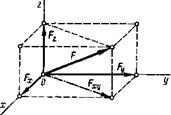Сложив эту равнодействующую с силой Р₃, получим равнодействующую трех сил:

+ F₃ = F₁+ F₂+ F₃

Повторив указанную операцию п—1 раз, получим равнодействующую системы п сил, которая будет равна векторной сумме этих сил; линия действия равнодействующей будет проходить через точку пересечения линий действия составляющих:

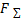= F ₁+ F₂ + F₃+ ... + 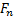или = ∑ .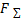

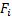Силовой многоугольник пространственной системы сил не лежит в одной плоскости, поэтому геометрический и графический способы нахождения равнодействующей неприемлемы, а применяется аналитический способ (метод проекций).

⇐ Предыдущая 1 2 3 456 7 8 Следующая ⇒