- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
равнодействующей плоской системы сходящихся сил
равнодействующей плоской системы сходящихся сил
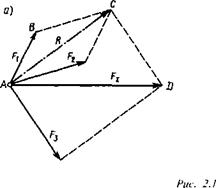
Система сил, линии действия которых лежат в одной плоскости и все пересекаются в одной точке, называется плоской системой сходящихся сил.
Теорема. Плоская система сходящихся сил в общем случае эквивалентна равнодействующей, которая равна векторной сумме этих сил; линия действия равнодействующей проходит через точку пересечения линий действия составляющих.
|
|
 Пусть дана плоская система трех сил F1 F2 и F3, линии действия которых сходятся в точке А. На основании следствия из аксиом III и IV перенесем эти силы вдоль линий их действия в точку А. Сложив первые две силы F1и F2 по правилу параллелограмма, получим их равнодействующую К (рис. 2.1, а):
Пусть дана плоская система трех сил F1 F2 и F3, линии действия которых сходятся в точке А. На основании следствия из аксиом III и IV перенесем эти силы вдоль линий их действия в точку А. Сложив первые две силы F1и F2 по правилу параллелограмма, получим их равнодействующую К (рис. 2.1, а):
R = F1+F2.
Пользуясь той же аксиомой параллелограмма, сложим равнодействующую R с силой F3:
FΣ=R+ F3 = F1+F2+F3,
где Рх — равнодействующая данной системы трех сил.
Аналогичные рассуждения можно провести для любого количества сходящихся сил, в результате чего получим
FΣ = F1 +F2 + F3+ …. + Fn.
Сокращенно это равенство запишем так:
FΣ = Σ Fi,
где / все целые числа от 1 до и, а греческая заглавная буква Е (сигма) означает сумму.
Очевидно, что построение, выполненное на рис. 2.1, а, можно заменить более простым (рис. 2.1,6). Многоугольник АВСИ называется силовым многоугольником. Сторона АО, соединяющая начало первого с концом последнего вектора, называется замыкающей стороной.
Необходимо помнить, что стрелки векторов слагаемых сил образуют определенное направление обхода по контуру силового многоугольника, а замыкающая сторона, определяющая модуль и направление равнодействующей, имеет стрелку, направленную против обхода (рис. 2.1,6).
Если определить равнодействующую с помощью геометрии и тригонометрии, то такой способ будет называться геометрическим.
Если сделать чертеж силового многоугольника в определенном масштабе, то равнодействующая определится простым измерением замыкающей стороны с последующим умножением на масштаб. Такой способ нахождения равнодействующей называется графическим.
Порядок сложения векторов при построении силового многоугольника на величину равнодействующей не влияет, так как векторная сумма от перемены мест слагаемых не меняется (рис. 2.1,6, многоугольник АВ1С10).
2 СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
Наука, изучающая расчеты конструкций на прочность, жесткость, устойчивость, называется сопротивлением материалов.
Все тела под действием сил деформируются, т.е. меняют форму и размер.
Упругие деформации- такие деформации, которые исчезают после снятия нагрузки.
Пластические деформации-деформации, которые остаются после снятия нагрузки.
Прочность- способность конструкции работать под действием нагрузки не разрушаясь и без пластических деформаций.
Жесткость-способность конструкций сопротивляться упругим деформациям.
Устойчивость-способность конструкций сохранять первоначальную форму упругого равновесия.
3 Резьбовые соединения
Резьбовыми называют соединения деталей с помощью резьбы. Они являются наиболее распространенным видом разъемных соединений. Резьбу имеют свыше 60 % деталей, применяемых в авиадвигателе. В конструкцию планера входит также большое число резьбовых деталей (например, при сборке планера тяжелого магистрального самолета используется свыше 150 тыс. болтов и винтов).
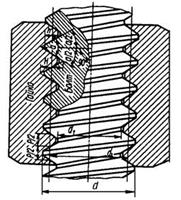
Резьба (рис. 5.12) – выступы, образованные на основной поверхности винтов и гаек и расположенные по винтовой линии.
|
Рис. 5.12. Резьбовое соединение
По форме основной поверхности различают цилиндрические и конические резьбы. Наиболее распространена цилиндрическая резьба. Коническую резьбу применяют для плотных соединений труб, масленок, пробок и т.п.
По профилю резьбы различают треугольные, прямоугольные, трапецеидальные, круглые и другие резьбы (рис. 5.13).
По направлению винтовой линии различают правую и левую резьбы. У правой резьбы винтовая линия идет слева направо и вверх, у левой – справа налево и вверх. Наиболее распространена правая резьба.
По числу заходов – однозаходная и многозаходная резьбы. Наиболее распространена однозаходная резьба.
Резьбу получают (формируют) методом резания, накатыванием (обработкой давлением), литьем и прессованием (композиционных материалов, порошков).
Основные геометрические параметры цилиндрических резьб включают: наружный d, средний d2 и внутренний d1 диаметры резьбы, шаг резьбы р, угол профиля α и число заходов n.
Метрическая резьба – основной вид резьбы крепежных деталей с углом профиля α = 60°. Она бывает с крупным и мелким шагом. Чаще всего выполняют наиболее износостойкую и технологичную резьбу с крупным шагом. Резьбы с мелким шагом характерны для тонкостенных изделий.
Трубные резьбы (цилиндрическая и коническая) служат для соединения труб и арматуры.
Трапецеидальная резьба технологична, отличается высокой прочностью витков и является основной для винтовых механизмов.
Упорная резьба имеет несимметричный профиль витков и выполняется на винтах, воспринимающих значительную одностороннюю нагрузку.
Прямоугольная резьба сложна в изготовлении и применяется редко.
Геометрические параметры резьб (кроме прямоугольной) и их допуски стандартизованы.
Билет 3
1 § 3.3. Момент силы относительно точки
Рассмотрим гайку, которую затягивают гаечным ключом определенной длины, прикладывая к концу ключа мускульное усилие. Если взять гаечный ключ в несколько раз длиннее, то прилагая то же усилие, гайку можно затянуть значительно сильнее. Из этого следует, что одна и та же сила может оказывать различное вращательное действие. Вращательное действие силы характеризуется моментом силы.
Понятие момента силы относительно точки ввел в механику итальянский ученый и художник эпохи Возрождения Леонардо да Винчи (1452—1519).
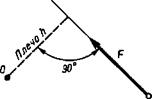
Моментом силы относительно точки называется произведение модуля силы на ее плечо (рис. 3.3):
М0(F) = Fh.
Точка, относительно которой берется момент, называется центром момента. Плечом силы относительно точки называется кратчайшее расстояние от центра момента до линии действия силы.
Единица момента силы:
[M] = [F] [h] = сила х длина = ньютон х метр = Н • м.
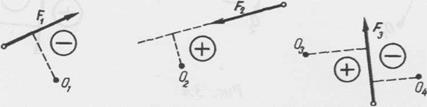
Условимся считать момент силы положительным, если сила стремится вращать свое плечо вокруг центра момента против часовой стрелки, и наоборот (рис. 3.4).
Одна и та же сила относительно разных точек может давать и положительный и отрицательный момент (рис. 3.4, сила F3). Рис.3..
2 ДОПУЩЕНИЯ В СОПРОТИВЛЕНИИ МАТЕРИАЛОВ:
1-е допущение.
допущение по материалам:
все материалы сплошные, однородные и изотропные (аморфность или независимость свойств от направлений),
в определенных пределах деформации материалов прямо пропорциональны величинам приложенных сил;
2-е допущение по конструкциям:
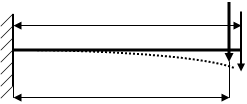
Принцип начальных размеров
 l
l
F
A F 
l1
При составлении условий равновесия МА пренебрегаем изменением в расположении сил, т.е. они незначительны по сравнению с размерами конструкций.
3-е допущение. В определенных пределах деформации прямо пропорциональны величинам приложенных сил.
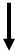

 F
F

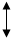













 Δ
Δ
2F
2Δ
Тела, подчиняющиеся этому принципу, называются линейно деформируемые.
4 - е допущение. В теле до приложения нагрузки нет внутренних (начальных) усилие
5– е допущение. Принцип независимости действия сил:
 Если на тело действует система сил, то деформация тела будет складываться из тех деформаций, которые бы имело тело под действием каждой из сил в отдельности.
Если на тело действует система сил, то деформация тела будет складываться из тех деформаций, которые бы имело тело под действием каждой из сил в отдельности.

 F
F

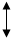













 Δ1
Δ1
 q
q




















Δ2
 q F
q F























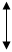



 Δ1+Δ2
Δ1+Δ2
 |
6 – е допущение. Принцип Сен- Венана.
В точках тела, достаточно удаленных от мест приложения нагрузок, величина внутренних сил весьма мало зависит от конкретного способа приложения этих нагрузок.
3Расчет напряженного болтового соединения, к которому после затяжки приложена внешняя осевая нагрузка.Рассматриваемый случай расчета характерен для большинства соединений (крепление крышек, фланцев). Такие соединения должны быть предельно плотными (крышки цилиндров), должны не допускать раскрытия стыка — появления зазора между соединяемыми деталями при приложении внешней нагрузки. Для выполнения данного требования предварительная затяжка болтов должна быть такой, чтобы после приложения рабочей нагрузки не произошло раскрытия стыка или нарушения плотности.
В зависимости от упругих свойств болтов и стягиваемых
деталей, а также от назначения соединения расчетную осевую нагрузку Р0 с учетом влияния крученая при затяжке принимают в пределах Р0 = (1,4—1,8) Р.
Приняв Р0 = 1 ,&Р, получим следующую формулу для определения расчетного диаметра резьбы:
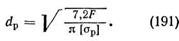
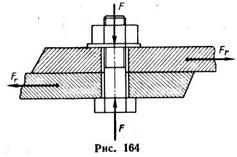
Резьбовое соединение, несущее поперечную нагрузку. На рис. 164
Билет 4
1 ПЛОСКАЯ СИСТЕМА ПРОИЗВОЛЬНО РАСПОЛОЖЕННЫХ СИЛ
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|