
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Свойства математического ожидания
Свойства математического ожидания
Свойство 1. Если 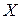 является постоянной величиной, то есть
является постоянной величиной, то есть 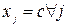 , то
, то 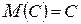 .
.
Свойство 2. Если 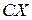 есть произведение случайной величины
есть произведение случайной величины 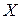 на постоянную
на постоянную 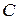 , то
, то 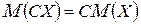 .
.
Свойство 3. Если 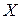 и
и 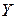 – случайные величины, то
– случайные величины, то 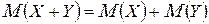 .
.
Свойство 4. Если 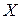 и
и 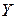 – независимые случайные величины, то
– независимые случайные величины, то 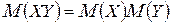 .
.
Свойство 5. Математическое ожидание 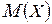 числа появлений события
числа появлений события 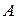 в
в 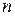 независимых испытаниях равно:
независимых испытаниях равно: 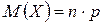 .
.
Свойство 6. 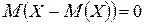 .
.
Определение 6. Дисперсией дискретной (ДСХ) случайной величины 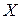 называют число
называют число 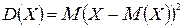 .
.
Свойства дисперсии.
Свойство 1. 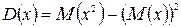 .
.
Свойство 2. Если случайная величина 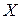 является постоянной
является постоянной 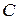 , то
, то 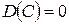 .
.
Свойство 3. 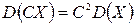 .
.
Свойство 4. Если 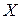 и
и 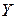 – независимые случайные величины, то
– независимые случайные величины, то 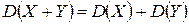 .
.
Свойство 5. Дисперсия суммы постоянной величины и случайной равна дисперсии случайной величины.
Свойство 6. Дисперсия числа появлений события 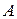 в
в 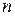 независимых испытаниях, в каждом из которых вероятность появления события
независимых испытаниях, в каждом из которых вероятность появления события 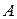 есть постоянная
есть постоянная 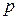 , равна
, равна 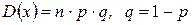 .
.
Определение 7. Средним квадратичным отклонением случайной величины 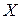 называют число
называют число 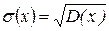 .
.
Закон больших чисел (теорема П. Л. Чебышева) в нестрогой формулировке: если число попарно независимых случайных величин достаточно велико, то их среднее арифметическое является практически постоянной величиной.
☼ЗАДАЧИ
ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
8.83. Стрелок производит три выстрела по цели. Вероятность попадания в цель при каждом выстреле равна 0,6. За каждое попадание стрелку дается 6 очков. Построить закон распределения числа полученных очков, найти математическое ожидание и дисперсию случайной величины.
8.84. Солдат ведет стрельбу по мишени до первого попадания, имея боезапас 5 патронов. Вероятность попадания при каждом выстреле равна 0,7. Построить закон распределения боезапаса, оставшегося неизрасходованным, найти математическое ожидание и дисперсию случайной величины.
8.85. Каждый из трёх стрелков стреляет по мишени один раз. Вероятности того, что первый, второй, третий стрелки попадут при одном выстреле в мишень, соответственно равны 0,5; 0,6; 0,7. Пусть 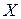 – общее число попаданий в мишень. Найти закон распределения
– общее число попаданий в мишень. Найти закон распределения 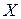 ,
, 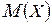 ,
, 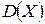 .
.
8.86. Решить задачу № 8.85 при условии, что четыре стрелка стреляют по мишени, а соответствующие вероятности попадания равны 0,5; 0,7; 0,8; 0,6.
8.87. В группе из 12 приборов имеется один бракованный. Чтобы его обнаружить, выбирают случайным образом один прибор за другим
и каждый выбранный прибор испытывают. Пусть 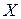 – число испытанных приборов (включая бракованный). Найти закон распределения,
– число испытанных приборов (включая бракованный). Найти закон распределения, 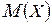 ,
, 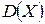 .
.
8.88. Запасные детали к машинам хранятся на специальном складе, на котором после аварии детали хранятся без порядка. Известно, что число испорченных деталей после аварии равно приблизительно 25%. Наугад берут 5 деталей. Найти биномиальный закон распределения случайной величины 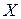 – числа испорченных деталей среди 5 отобранных и вычислить
– числа испорченных деталей среди 5 отобранных и вычислить 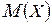 ,
, 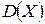 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|