Классическое определение вероятности

Классическое определение вероятности

Вероятностью 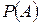события 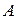называется отношение числа 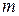благоприятствующих этому событию исходов к общему числу 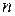всех несовместных, единственно возможных и равновозможных элементарных исходов испытания.

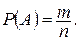
1. Из слова «балалайка» наудачу выбирают букву. Какова вероятность того, что эта буква окажется: а) гласной; б) согласной?

Общее количество исходов равно 9. Гласных букв в слове – 4, согласных – 4. Поэтому вероятность в обоих случаях равна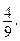

Статистическое определение вероятности

Относительной частотой 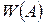события 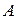называется отношение числа 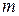испытаний, в которых появилось событие 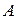, к общему числу 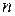проведенных испытаний: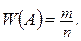

Статистической вероятностью события 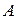называют его относительную частоту 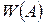или число, близкое к ней.

☼ЗАДАЧИ

ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

8.54. Брошена игральная кость. Найти вероятность того, что выпадет число очков, кратное 3.

8.55. В ящике имеется 40 одинаковых деталей, из них 8 окрашенных. Наугад берут 3 детали. Найти вероятность того, что все три детали окажутся окрашенными.

8.56. В мешочке имеется 7 белых шаров, подписанных буквами а, б, г, д, л, о, н. Эти семь шаров извлекают по одному. Какова вероятность, что в результате такого вытаскивания получится слово «гандбол»?

8.57. Коля хочет позвонить другу, но забыл при этом две последние цифры его пятизначного номера телефона. Какова вероятность, что Коля наберет правильный номер, если он знает, что все цифры номера – разные?

8.58. Монета брошена три раза. Найти вероятность того,

а) что хотя бы один раз появится герб;

б) что герб не появится ни разу.

8.59. В ящике содержится 5 одинаковых кубиков, занумерованных цифрами от 1 до 5.

а) Найти вероятность того, что номера извлеченных кубиков появятся в следующем порядке: 1, 5, 4, 2, 3.

б) Наугад извлечены 3 кубика. Найти вероятность того, что среди извлеченных кубиков окажутся кубики № 1 и № 4.

8.60. В одном ящике 5 белых и 3 красных шарика, в другом – 6 белых и 4 красных. Из каждого ящика наугад вынимается по одному шарику. Чему равна вероятность того, что: а) оба шарика окажутся красными; б) оба шарика окажутся белыми; в) оба шарика окажутся разноцветными?

8.61. В классе учатся 20 мальчиков и 10 девочек. Зачет по теории вероятности вызвались досрочно сдавать 12 учеников. Найти вероятность того, что среди них: а) не окажется ли одного мальчика; б) не окажется ни одной девочки; в) окажется 6 девочек.

8.62. Кейс имеет 2 секретных замка, каждый из которых имеет на оси 3 диска, причем каждый диск разделен на 9 секторов, занумерованных цифрами от 1 до 9. Замок открывается лишь тогда, когда диски установлены так, что их номера образуют определенное трехзначное число. Найти вероятность того, что при произвольной установке дисков можно: 1) открыть только левый замок; 2) открыть кейс.

8.63. Монета была брошена 250 раз. При этом герб появился 128 раз. Найти относительную частоту появления герба.

8.64. Орудие произвело 30 выстрелов по мишени. Зафиксировано 12 попаданий. Найти относительную частоту попадания в мишень.

8.65. Отдел технического контроля из 300 проверенных деталей обнаружил 3 нестандартные. Найти относительную частоту появления нестандартных деталей.

⇐ Предыдущая 1 2 345 6 7 Следующая ⇒